Log-concavity and strong q-log-convexity for Riordan arrays and recursive matrices
Published online by Cambridge University Press: 14 August 2017
Extract
Let [An,k]n,k⩾0 be an infinite lower triangular array satisfying the recurrence
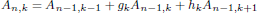
for n ⩾ 1 and k ⩾ 0, where A0,0 = 1, A0,k = Ak,–1 = 0 for k > 0. We present some criteria for the log-concavity of rows and strong q-log-convexity of generating functions of rows. Our results can be applied to many well-known triangular arrays, such as the Pascal triangle, the Stirling triangle of the second kind, the Bell triangle, the large Schröder triangle, the Motzkin triangle, and the Catalan triangles of Aigner and Shapiro, in a unified approach. In addition, we prove that the binomial transformation not only preserves the strong q-log-convexity property, but also preserves the strong q-log-concavity property. Finally, we demonstrate that the strong q-log-convexity property is preserved by the Stirling transformation and Whitney transformation of the second kind, which extends some known results for the strong q-log-convexity property.
- Type
- Research Article
- Information
- Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 147 , Issue 6 , December 2017 , pp. 1297 - 1310
- Copyright
- Copyright © Royal Society of Edinburgh 2017
- 11
- Cited by




