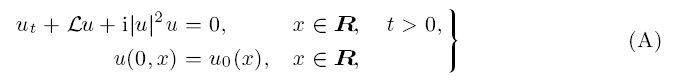We study the Cauchy problem for the nonlinear Schrödinger equation with dissipation where L is a linear pseudodifferential operator with dissipative symbol ReL(ξ) ≥ C1|ξ|2/(1 + ξ2) and |L′(ξ)| ≤ C2(|ξ|+ |ξ|n) for all ξ ∈ R. Here, C1, C2 > 0, n ≥ 1. Moreover, we assume that L(ξ) = αξ2 + O(|ξ|2+γ) for all |ξ| < 1, where γ > 0, Re α > 0, Im α ≥ 0. When L(ξ) = αξ2, equation (A) is the nonlinear Schrödinger equation with dissipation ut − αuxx + i|u|2u = 0. Our purpose is to prove that solutions of (A) satisfy the time decay estimate 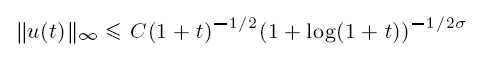under the conditions that u0 ∈ Hn,0 ∩ H0,1 have the mean value 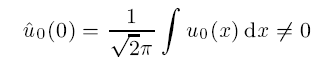and the norm ‖u0‖Hn,0 + ‖u0‖H0,1 = ε is sufficiently small, where σ = 1 if Im α > 0 and σ = 2 if Im α = 0, and 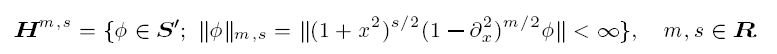Therefore, equation (A) is considered as a critical case for the large-time asymptotic behaviour because the solutions of the Cauchy problem for the equation ut − αuxx + i|u|p−1u = 0, with p > 3 have the same time decay estimate ‖u‖L∞ = O(t−½) as that of solutions to the linear equation. On the other hand, note that solutions of the Cauchy problem (A) have an additional logarithmic time decay. Our strategy of the proof of the large-time asymptotics of solutions is to translate (A) to another nonlinear equation in which the mean value of the nonlinearity is zero for all time.