Hostname: page-component-77c89778f8-vpsfw Total loading time: 0 Render date: 2024-07-17T12:07:55.328Z Has data issue: false hasContentIssue false
  • English
  • Français

IV.—On an Elementary Solution of a Partial Differential Equation of Parabolic Type. Part I

Published online by Cambridge University Press:  14 February 2012

E. T. Copson
E. T. Copson
Affiliation:
University College, Dundee, in the University of St Andrews.
Get access Rights & Permissions [Opens in a new window]

Summary

Professor E. T. Whittaker has recently discovered a Third Quantum-Mechanical Principal Function R(q, Q, t - T) and has worked out the theory of this function in detail when the Hamiltonian is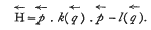

By using the Sturm-Liouville theory of linear differential equations and the properties of Green's function, it is shown that the function is an elementary solution of the adjoint of the Schrodinger wave equation associated with the Hamiltonian H.

It is pointed out that the modified Planck constant ħ arises solely from the commutation relation 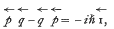and may, from the analytical view-point, be any constant, real or complex. In particular, if ħ = i, the use of an algebra with the commutation relation 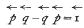leads to an elementary solution of the real equation of parabolic type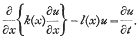

Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 61 , Issue 1 , 1941 , pp. 37 - 53
Copyright
Copyright © Royal Society of Edinburgh 1941

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

References to Literature

Courant, R., and Hilbert, D., 1931. Methoden der mathematischen Physik, I (Zweite Auflage), Berlin.CrossRefGoogle Scholar
Gevrey, M., 1913. “Sur les équations aux dérivées du type parabolique,” Journ. Math., pures appl., vol. ix, pp. 305–471.Google Scholar
Gevrey, M., 1914. “Sur les équations aux dérivées du type parabolique (suite),” Journ. Math., pures appl., vol. x, pp. 105–148.Google Scholar
Goursat, É., 1923. Cours d'Analyse, III (3ème Édition), Paris.Google Scholar
Hadamard, J., 1911. “Sur la solution fondamentale des équations aux dérivées partielles du type parabolique,” C.R. Acad. Sci. Paris, vol. clii, pp. 1148–1149.Google Scholar
Hilbert, D., 1924. Grundzüge einer allgemeiner Theorie der linearen Integralgleichungen (Zweite Auflage), Leipzig.Google Scholar
Hobson, E. W., 1926. The Theory of Functions of a Real Variable, II (2nd ed.), Cambridge.Google Scholar
Ince, E. L., 1927. Ordinary Differential Equations, London.Google Scholar
Kepinski, S., 1905. “Über die Differentialgleichung Math. Ann., vol. lxi, pp. 397–405.CrossRefGoogle Scholar
Oseen, C. W., 1911-1912. “Neue Lösung der Sommerfeldschen Diffraktionsproblems, I,” Ark. Mat. Astr. Fys., vol. vii, no. 25.Google Scholar
Oseen, C. W., 1930-1932. “Über die Fundamentalintegrale einiger wellenmechanischen Differentialgleichungen,” Ark. Mat. Astr. Fys., vol. xxii, A, no. 2.Google Scholar
Picard, É, 1927. Leçons sur quelques types simples d'équations aux dérivées partielles, Paris.Google Scholar
Rothe, E., 1931. “Über die Grundlösung bei parabolischen Gleichungen,” Math. Zeits., vol. xxxiii, pp. 488–504.CrossRefGoogle Scholar
Whittaker, E. T., 1940. “On Hamilton's Principal Function in Quantum Mechanics,” Proc. Roy. Soc. Edin., vol. lxi, A, pp. 1–19.Google Scholar
Whittaker, E. T., and Watson, G. N., 1920. Modern Analysis (3rd ed.), Cambridge.Google Scholar