Hostname: page-component-76fb5796d-2lccl Total loading time: 0 Render date: 2024-04-27T00:35:57.872Z Has data issue: false hasContentIssue false
  • English
  • Français

The Fourier extension operator of distributions in Sobolev spaces of the sphere and the Helmholtz equation

Part of: Linear function spaces and their duals Harmonic analysis in several variables Elliptic equations and systems

Published online by Cambridge University Press:  16 November 2020

J. A. Barceló ,
M. Folch-Gabayet ,
T. Luque ,
S. Pérez-Esteva  and
M. C. Vilela
J. A. Barceló
Affiliation:
Departamento de Matemática e Informática aplicadas a las Ingenierías Civil y Naval, Universidad Politécnica de Madrid, Madrid, 28040, Spain (juanantonio.barcelo@upm.es)
M. Folch-Gabayet
Affiliation:
Universidad Nacional Autónoma de México, Ciudad Universitaria, Ciudad de México, 04510, México (folchgab@matem.unam.mx)
T. Luque
Affiliation:
Departamento de Análisis Matemático y Matemática Aplicada, Universidad Complutense de Madrid, Madrid, 28040, Spain (t.luque@ucm.es)
S. Pérez-Esteva
Affiliation:
Instituto de Matemáticas, Unidad de Cuernavaca, Universidad Nacional Autónoma de México, México (spesteva@im.unam.mx)
M. C. Vilela
Affiliation:
ETSI Navales, Departamento de Matemática e Informática aplicadas a las Ingenierías Civil y Naval, Universidad Politécnica de Madrid, Madrid, 28040, Spain (maricruz.vilela@upm.es)
Get access Rights & Permissions [Opens in a new window]

Abstract

The purpose of this paper is to characterize the entire solutions of the homogeneous Helmholtz equation (solutions in ℝd) arising from the Fourier extension operator of distributions in Sobolev spaces of the sphere 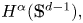$H^\alpha (\mathbb {S}^{d-1}),$ with α ∈ ℝ. We present two characterizations. The first one is written in terms of certain L2-weighted norms involving real powers of the spherical Laplacian. The second one is in the spirit of the classical description of the Herglotz wave functions given by P. Hartman and C. Wilcox. For α > 0 this characterization involves a multivariable square function evaluated in a vector of entire solutions of the Helmholtz equation, while for α < 0 it is written in terms of an spherical integral operator acting as a fractional integration operator. Finally, we also characterize all the solutions that are the Fourier extension operator of distributions in the sphere.

Keywords

Fourier extension operatorHerglotz wave functionHelmholtz equation

MSC classification

Primary: 35J05: Laplacian operator, reduced wave equation (Helmholtz equation), Poisson equation
Secondary: 42B10: Fourier and Fourier-Stieltjes transforms and other transforms of Fourier type 46E35: Sobolev spaces and other spaces of “smooth” functions, embedding theorems, trace theorems
Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 151 , Issue 6 , December 2021 , pp. 1768 - 1789
Check for updates
Copyright
Copyright © The Author(s), 2020. Published by Cambridge University Press on behalf of The Royal Society of Edinburgh

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Álvarez, J., Folch–Gabayet, M. and Pérez-Esteva, S.. Banach spaces of solutions of the Helmholtz equation in the plane. J. Fourier Anal. Appl. 7 (2001), 49–62.CrossRefGoogle Scholar
Atkinson, K. and Han, W.. Spherical Harmonics and Approximations on the Unit Sphere: An Introduction. Lecture Notes in Math. 2044, 137–172 (Berlin: Springer, 2012).CrossRefGoogle Scholar
Axler, S., Bourdon, P. and Ramey, W.. Harmonic Function Theory. In Graduate Texts in Mathematics (eds S. Axler, F.W. Gehring and K.A. Ribet), 2nd edn, vol. 137, pp. 9–16 (New York: Springer-Verlag, 2001).Google Scholar
Barceló, J. A., Ruiz, A. and Vega, L.. Weighted estimates for the Helmholtz equation and some applications. J. Funct. Anal., 150 (1997), 151–218.CrossRefGoogle Scholar
Barceló, J. A., Bennett, J. M. and Ruiz, A.. Mapping properties of a projection related to the Helmholtz Equation. J. Fourier Anal. Appl. 9 (2003), 541–562.CrossRefGoogle Scholar
Barceló, J. A., Luque, T. and Pérez-Esteva, S.. Characterization of Sobolev spaces on the sphere. J. Math. Anal. Appl. 491 (2020)CrossRefGoogle Scholar
Colton, D. and Kress, R.. Inverse Acoustic and Electromagnetic Scattering Theory. (Springer-Verlag Berlin Heidelberg 1992, 1998. Printed in Germany)CrossRefGoogle Scholar
Hartman, P. and Wilcox, C.. On solutions of the Helmholtz equation in exterior domains. Math. Zeitschr. 75 (1961), 228–255.CrossRefGoogle Scholar
Helgason, H. S.. Topics in Harmonic Analysis on Homogeneous Spaces. (Boston: Birkhäuser, 1981).Google Scholar
Lebedev, N. N.. Special functions and their applications. (New York: Dover Publications Inc., 1972).Google Scholar
Lemoine, C.. Fourier transforms of homogeneous distribution. Annali della Scuola Normale Superiore di Pisa, Classe di Scienze 3esérie, tome 26 (1972), 117–149.Google Scholar
Pérez-Esteva, S. and Valenzuela-Díaz, S.. Reproducing kernel for the Herglotz functions in ℝn and solutions of the Helmholtz equation. J. Fourier Anal. Appl. 23 (2017), 834–862.CrossRefGoogle Scholar