Article contents
Focusing blow-up for quasilinear parabolic equations
Published online by Cambridge University Press: 14 November 2011
Abstract
We study the behaviour of the non-negative blowing up solutions to the quasilinear parabolic equation with a typical reaction–diffusion right-hand side and with a singularity in the space variable which takes the form
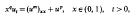
where m ≧ 1, p > 1 are arbitrary constants, in the critical exponent case q = (p–1)/m > 0. We impose zero Dirichlet boundary conditions at the singular point x = 0 and at x = 1, and take large initial data. For a class of ‘concave’ initial functions, we prove focusing at the origin of the solutions as t approaches the blow-up time T in the sense that x = 0 belongs to the blow-up set. The proof is based on an application of the intersection comparison method with an explicit ‘separable’ solution which has the same blow-up time as u. The method has a natural generalisation to the case of more general nonlinearities in the equation. A description of different fine structures of blow-up patterns in the semilinear case m = 1 and in the quasilinear one m > 1 is also presented. A numerical study of the semilinear equation is also made using an adaptive collocation method. This is shown to give very close agreement with the fine structure predicted and allows us to make some conjectures about the general behaviour.
- Type
- Research Article
- Information
- Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 128 , Issue 5 , 1998 , pp. 965 - 992
- Copyright
- Copyright © Royal Society of Edinburgh 1998
References
- 7
- Cited by




