No CrossRef data available.
Article contents
Estimates on the Green's function of second-order elliptic operators in ℝN
Published online by Cambridge University Press: 14 November 2011
Abstract
Sharp upper and lower pointwise bounds are obtained for the Green's function of the equation
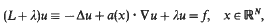
for λ> 0. Initially, in a Cartesian frame, it is assumed that 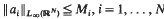 . Pointwise estimates for the heat kernel of ut + Lu = 0, recently obtained under this assumption, are Laplace-transformed to yield corresponding elliptic results. In a second approach, the coordinate-free constraint
. Pointwise estimates for the heat kernel of ut + Lu = 0, recently obtained under this assumption, are Laplace-transformed to yield corresponding elliptic results. In a second approach, the coordinate-free constraint 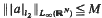 is imposed. Within this class of operators, the equations defining the maximal and minimal Green's functions are found to be simple ODEs when written in polar coordinates, and these are soluble in terms of the singular Kummer confluent hypergeometric function. For both approaches, bounds on
is imposed. Within this class of operators, the equations defining the maximal and minimal Green's functions are found to be simple ODEs when written in polar coordinates, and these are soluble in terms of the singular Kummer confluent hypergeometric function. For both approaches, bounds on 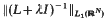 are derived as a consequence.
are derived as a consequence.
- Type
- Research Article
- Information
- Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 128 , Issue 5 , 1998 , pp. 1033 - 1051
- Copyright
- Copyright © Royal Society of Edinburgh 1998




