Hostname: page-component-8448b6f56d-cfpbc Total loading time: 0 Render date: 2024-04-19T22:55:40.863Z Has data issue: false hasContentIssue false
  • English
  • Français

Estimate, existence and nonexistence of positive solutions of Hardy–Hénon equations

Part of: Partial differential equations Elliptic equations and systems

Published online by Cambridge University Press:  18 May 2021

Xiyou Cheng ,
Lei Wei  and
Yimin Zhang
Xiyou Cheng
Affiliation:
School of Mathematics and Statistics, Lanzhou University, Lanzhou, Gansu730000, China (chengxy03@163.com)
Lei Wei
Affiliation:
School of Mathematics and Statistics, Jiangsu Normal University, Xuzhou, Jiangsu221116, China (wlxznu@163.com)
Yimin Zhang
Affiliation:
Center for Mathematical Sciences and Department of Mathematics, Wuhan University of Technology, Wuhan430070, China (zhangym802@126.com)
Get access Rights & Permissions [Opens in a new window]

Abstract

We consider the boundary Hardy–Hénon equation

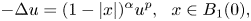\[ -\Delta u=(1-|x|)^{\alpha} u^{p},\ \ x\in B_1(0), \]
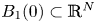where $B_1(0)\subset \mathbb {R}^{N}$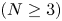$(N\geq 3)$ is a ball of radial 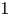$1$ centred at 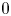$0$, 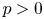$p>0$ and 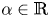$\alpha \in \mathbb {R}$. We are concerned with the estimate, existence and nonexistence of positive solutions of the equation, in particular, the equation with Dirichlet boundary condition. For the case 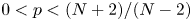$0< p<({N+2})/({N-2})$, we establish the estimate of positive solutions. When 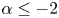$\alpha \leq -2$ and 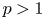$p>1$, we give some conclusions with respect to nonexistence. When 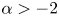$\alpha >-2$ and 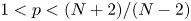$1< p<({N+2})/({N-2})$, we obtain the existence of positive solution for the corresponding Dirichlet problem. When $0< p\leq 1$ and 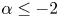$\alpha \leq -2$, we show the nonexistence of positive solutions. When 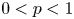$0< p<1$, 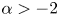$\alpha >-2$, we give some results with respect to existence and uniqueness of positive solutions.

Keywords

SingularityEstimateExistenceNonexistence

MSC classification

Primary: 35J61: Semilinear elliptic equations
Secondary: 35A09: Classical solutions 35B09: Positive solutions 35B45: A priori estimates
Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 152 , Issue 2 , April 2022 , pp. 518 - 541
Check for updates
Copyright
Copyright © The Author(s), 2021. Published by Cambridge University Press on behalf of The Royal Society of Edinburgh

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Bandle, C., Moroz, V. and Reichel, W.. ‘Boundary blowup’ type sub-solutions to semilinear elliptic equations with Hardy potential. J. London Math. Soc. 77 (2008), 503–523.CrossRefGoogle Scholar
Bandle, C. and Pozio, M. A.. Sublinear elliptic problems with a Hardy potential. Nonlinear Anal. 119 (2015), 149–166.CrossRefGoogle Scholar
Brezis, H. and Marcus, M.. Hardy's inequalities revisited. Ann. Sc. Norm. Super. Pisa Cl. Sci. 25 (1997), 217–237.Google Scholar
Cao, D., Peng, S. and Yan, S.. Asymptotic behaviour of ground state solutions for the Hénon equation. IMA J. Appl. Math. 74 (2009), 468–480.CrossRefGoogle Scholar
Chen, W. and Li, C.. Classification of solutions of some nonlinear elliptic equations. Duke Math. J. 63 (1991), 615–622.CrossRefGoogle Scholar
Dancer, E., Du, Y. and Guo, Z. M.. Finite Morse index solutions of an elliptic equation with supercritical exponent. J. Diff. Equ. 250 (2011), 3281–3310.CrossRefGoogle Scholar
Du, Y.. Order structure and topological methods in nonlinear partial differential equations. Maximum principle and applications, vol 1, Fang-Hua Lin (Courant Institute of Math. Sci., New York University) (Series ed.) (Singapore: World Scientific Publishing, 2006).Google Scholar
Du, Y. and Guo, Z. M.. Positive solutions of an elliptic equation with negative exponent: stability and critical power. J. Diff. Equ. 246 (2009), 2387–2414.CrossRefGoogle Scholar
Du, Y. and Wei, L.. Boundary behavior of positive solutions to nonlinear elliptic equations with Hardy potential. J. London Math. Soc. 91 (2015), 731–749.CrossRefGoogle Scholar
Gidas, B., Ni, W. M. and Nirenberg, L.. Symmetry and related properties via the maximum principle. Commun. Math. Phys. 68 (1979), 209–243.CrossRefGoogle Scholar
Gidas, B. and Spruck, J.. Global and local behavior of positive solutions of nonlinear elliptic equations. Commun. Pure Appl. Math. 6 (1981), 883–901.Google Scholar
Marcus, M., Mizel, V. and Pinchover, Y.: On the best constant for Hardy's inequality in $R^{N}$. Trans. Amer. Math. Soc. 350(1998), 3237–3255.CrossRefGoogle Scholar
Mercuri, C. and dos Santos, E. M.. Quantitative symmetry breaking of groundstates for a class of weighted Emden-Fowler equations. Nonlinearity 32 (2019), 4445–4464.CrossRefGoogle Scholar
Phan, Q. and Souplet, P.. Liouville-type theorems and bounds of solutions of Hardy-Hénon equations. J. Diff. Equ. 252 (2012), 2544–2562.CrossRefGoogle Scholar