We consider non-negative solutions of the Cauchy problem for quasilinear parabolic equations ut = Δum + f(u), where m > 1 and f(ξ) is a positive function in ξ > 0 satisfying f(0) = 0 and a blow-up condition

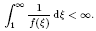
We show that if ξm+2/N /(−log ξ)β = O(f(ξ)) as ξ ↓ 0 for some 0 < β < 2/(mN + 2), one of the following holds: (i) all non-trivial solutions blow up in finite time; (ii) every non-trivial solution with an initial datum u0 having compact support exists globally in time and grows up to ∞ as t → ∞: limtt→∞ inf|x|<Ru(x, t) = ∞ for any R > 0. Moreover, we give a condition on f such that (i) holds, and show the existence of f such that (ii) holds.