Hostname: page-component-7479d7b7d-k7p5g Total loading time: 0 Render date: 2024-07-12T20:21:20.506Z Has data issue: false hasContentIssue false
  • English
  • Français

The Schrödinger equation as a singular perturbation problem†

Published online by Cambridge University Press:  14 November 2011

E. M. de Jager  and
T. Küpper
E. M. de Jager
Affiliation:
Department of Mathematics, University of Amsterdam, Netherlands
T. Küpper
Affiliation:
Department of Mathematics, University of Cologne, Germany
Get access Rights & Permissions [Opens in a new window]

Synopsis

Comparisons have been made of the eigenvalues and the corresponding eigenfunctions of the eigenvalue problems

and

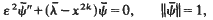
with φ ∈ C(-∞, +∞) and 0≦φ(x)≦C|x|i+1(1+|x|1), −∞<x<+∞ where i and l are arbitrary positive numbers with i≧2k≧2, k integer. In first approximation the eigenvalues λ and λ− and the corresponding eigenfunctions ψ and ψ are the same for ε→0; the error decreases whenever the exponent i increases.

Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 82 , Issue 1-2 , 1978 , pp. 1 - 11
Copyright
Copyright © Royal Society of Edinburgh 1978

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1Eckhaus, W.. Matched asymptotic expansions and singular perturbations (Amsterdam: North Holland, 1973).Google Scholar
2Imada, N.. An asymptotic solution of a second order linear differential equation. J. Math. Anal. Appl. 52 (1975), 322–343.CrossRefGoogle Scholar
3Giertz, M.. On the solutions in L 2(-∞, +∞) of y n + (λ-q(x)) y = 0 when q is rapidly increasing. Proc. London Math. Soc. 14 (1964), 53–73.CrossRefGoogle Scholar
4Kato, T.. Perturbation theory for linear operators (Berlin: Springer, 1976).Google Scholar
5Kemble, E.. The fundamental principles of quantum mechanics (New York: Dover, 1937).Google Scholar
6Pitts, C. G. C.. Asymptotic approximations to solutions of a second-order differential equation. Quart. J. Math. Oxford Ser. 17 (1966), 307–320.Google Scholar
7Pitts, C. G. C.. Simplified asymptotic approximations to solutions of a second-order differential equation. Quart. J. Math. Oxford Ser. 21 (1970), 223–242.CrossRefGoogle Scholar
8Pitts, C. G. C.. On eigenfunction expansions for a positive potential function increasing slowly to infinity. J. Differential Equations, 13 (1973), 358–373.CrossRefGoogle Scholar
9Titchmarsh, E. C.. Eigenfunction expansions associated with second order differential equations I (Oxford: Clarendon Press, 1962).Google Scholar
10Titchmarsh, E. C.. Eigenfunction expansions associated with second order differential equations II (Oxford: Clarendon Press, 1958).Google Scholar
11Titchmarsh, E. C.. On the asymptotic distribution of eigenvalues. Quart. J. Math. Oxford Ser. 5 (1954), 228–240.CrossRefGoogle Scholar
12Weinstein, A. and Stenger, W.. Methods of intermediate problems for eigenvalues (London: Academic Press, 1972).Google Scholar