Hostname: page-component-77c89778f8-rkxrd Total loading time: 0 Render date: 2024-07-19T16:17:47.671Z Has data issue: false hasContentIssue false
  • English
  • Français

Classes of groups related to Fa,b,c*

Published online by Cambridge University Press:  14 November 2011

C. M. Campbell  and
E. F. Robertson
C. M. Campbell
Affiliation:
Mathematical Institute, University of St Andrews
E. F. Robertson
Affiliation:
Mathematical Institute, University of St Andrews
Get access Rights & Permissions [Opens in a new window]

Synopsis

Groups 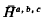having two generators and two relations are studied. The Reidemeister-Schreier algorithm is used to determine presentations for their derived groups. This enables the orders of the groups 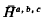to be found. Necessary and sufficient conditions are given for the groups to be metabelian. Certain classes closely related to the class 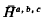are also discussed.

Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 78 , Issue 3-4 , 1978 , pp. 209 - 218
Copyright
Copyright © Royal Society of Edinburgh 1978

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

*

This paper was assisted in publication by a grant from the Carnegie Trust for the Universities of Scotland.

References

1 Beetham, M. J. and Campbell, C. M.. A note on the Todd-Coxeter coset enumeration algorithm. Proc. Edinburgh Math. Soc. 20 (1976), 73–79.Google Scholar
2 Brunner, A. M.. The determination of Fibonacci groups. Bull. Austral. Math. Soc. 11 (1974), 11–14.Google Scholar
3 Campbell, C. M., Coxeter, H. S. M. and Robertson, E. F.. Some families of finite groups having two generators and two relations. Proc. Roy. Soc. London Ser. A, to appear.Google Scholar
4 Conway, J. H., Coxeter, H. S. M. and Shephard, G. C.. The centre of a finitely generated group. Tensor 25 (1972), 405–418.Google Scholar
5 Coxeter, H. S. M.. The binary polyhedral groups and other generalisations of the quaternion group. Duke Math. J. 7 (1940), 367–379.CrossRefGoogle Scholar
6 Coxeter, H. S. M. and Moser, W. O. J.. Generators and relationsfor discrete groups 3rd edn (Berlin: Springer, 1972).Google Scholar
7 Johnson, D. L.. Some infinite Fibonacci groups. Proc. Edinburgh Math. Soc. 19 (1975), 311–314.CrossRefGoogle Scholar
8 Johnson, D. L. and Mawdesley, H.. Some groups of Fibonacci type. J. Austral. Math. Soc. Ser. A 20 (1975), 199–204.Google Scholar
9 Johnson, D. L., Wamsley, J. W. and Wright, D.. The Fibonacci groups. Proc. London Math. Soc. 29 (1974), 577–592.Google Scholar