Article contents
18.—Singular Linear Differential Operators with many Parameters*
Published online by Cambridge University Press: 14 February 2012
Synopsis
It is the purpose of this paper to make a study of the solutions of the following k-formally self-adjoint differential equations
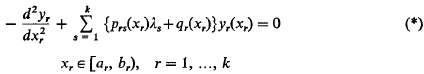
where ar, br), r = 1, 2, …, k, denote k semi-open intervals in which ar is finite and br is arbitrary and the λs, s = 1, 2, …, k, are spectral parameters.
The main theme of the paper is that of extending the Hermann Weyl limit-point, limit-circle theory to the multi-parameter case. That is we consider under which circumstances there exist, for each r, one or two solutions yr(xr) of (*) which are square integrable in a suitably defined Hilbert space Hr. This is then generalised to consider the problem of investigating the possibility of the product
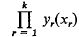
of solutions of (*) being square integrable in H, the tensor product of the separate spaces Hr. The analyticky of the corresponding generalised Hermann Weyl coefficients mr(λ1, λ2,…, λk), r = 1,…, k, is also investigated. Some examples illustrating the theory are given and an alternative formulation of the problem is suggested.
- Type
- Research Article
- Information
- Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 71 , Issue 3 , 1973 , pp. 199 - 232
- Copyright
- Copyright © Royal Society of Edinburgh 1973
References
References to Literature
- 2
- Cited by




