Article contents
On the Stieltjes Integral
Published online by Cambridge University Press: 20 January 2009
Extract
The conception of the integral of one function with respect to another was introduced by Stieltjes in his classical memoir on continued fractions. He denned the integral as
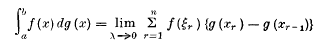
and gave the formula for integration by parts.
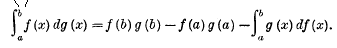
- Type
- Research Article
- Information
- Copyright
- Copyright © Edinburgh Mathematical Society 1929
References
page 209 note 1 Ann. de la Fac. des Sc de Toulouse, 8 (1894). A full account of the Riemann- Stieltjes integral has been given by Pollard, Quarterly Journal, 49 (1923), 73. In the definition (![]() ) is any subdivision of (a, b) and λ is the length of the longest interval (x r−1, x r).
) is any subdivision of (a, b) and λ is the length of the longest interval (x r−1, x r).
page 209 note 2 See especially the account given by Lebesgue, Leçons sur l'Intégration (2nd Ed.), Chapter 11 (1928). Also papers by Hildebrandt, , Bull. Amer. Math. Soc. (2), 24 (1918), 177CrossRefGoogle Scholar; and Francis, , Proc. Camb. Phil. Soc., 22 (1925), 935.CrossRefGoogle Scholar
page 209 note 3 Another method of defining the integral has been developed by Daniell, P. J ., Annals of Math., 19 (1918)CrossRefGoogle Scholar, 279; 21 (1920), 219; 23 (1923), 169, which can be employed in certain cases when g(x) is not of bounded variation. Starting with g(x), a class of functions f(x) is found for which the integral can be defined.
page 210 note 1 Comptes Rendus, 169 (1919), 219.Google Scholar
page 209 note 2 Proc. Edin. Math. Soc., 44 (1926), 79.Google Scholar
page 211 note 1 Ann. de l'École Normale, 33 (1916), 157. Denjoy does not discuss the conception in detail, another function, “la variation simple,” being more convenient in his work. Francis, E. C., Proc. Camb. Phil. Soc., 22 (1925), 924, has given an extension of the mean value theorem in which “la variation simple ” is employed, but the theorem given below seems a more direct generalisation.CrossRefGoogle Scholar
page 211 note 2 Cf. Hobson, , Functions of a Real Variable (1921), 1 451.Google Scholar
page 214 note 1 Proc. Edin. Math. Soc., 44 (1926), 79.Google Scholar For the case of φ (x) = x see Whittaker, J. M., Proc. Lond. Math. Soc., (2) 25 (1926), 213.CrossRefGoogle ScholarEttlinger, H. J., Journal Lond. Math. Soc., 2 (1927), 245,CrossRefGoogle Scholar and Miss R. C. Young, ibid., 3 (1928), 117. The latter shows that the theorem is true in space of n dimensions.
page 214 note 2 Hobson, , op. cit., 102.Google Scholar
page 216 note 1 Hobson, , op. cit., 621. Theorem 2 has been emended in accordance with a suggestion of Dr Hyslop.Google Scholar
page 219 note 1 If f'(x) is not bounded below, (1) is certainly true if mQ>0. If mQ = 0 and sQ>0 (<0) it can be inferred that f' (x) is not bounded above (below).
page 222 note 1 Cf. Hobson, , op. cit., 585.Google Scholar
page 225 note 1 Cf. Pollard, , loc. cit.Google Scholar
page 227 note 1 Hobson, , op. cit., 2, 144Google Scholar.
page 225 note 2 Hobson, , op. cit., 541Google Scholar.
page 229 note 1 Fundamenta Math., 11 (1928), 27.CrossRefGoogle Scholar
page 229 note 2 Theorems of the same type involving the Stieltjes integral projier have been given by Hahn, , Monatshefte für Math. u. Physik, 32 (1922), 84.Google Scholar
page 232 note 1 If g(x) is assumed to be continuous the integrals exist as ordinary Stieltjes integrals, and f(x) need not be continuous. Cf. Whittaker, J. M., Proc. Edin. Math. Soc. (2), 1 (1928), 169.CrossRefGoogle Scholar
page 232 note 2 Cf. Hobson, , op. cit., 2, 579Google Scholar.
page 232 note 3 Hobson, , op. cit., 1, 317.Google Scholar
page 233 note 1 Hobson, , op. cit., 2, 557.Google Scholar
- 1
- Cited by




