No CrossRef data available.
Article contents
Numerical Approximations to Extremal Toric Kähler Metrics with Arbitrary Kähler Class
Published online by Cambridge University Press: 10 January 2017
Abstract
We develop new algorithms for approximating extremal toric Kähler metrics. We focus on an extremal metric on 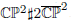 , which is conformal to an Einstein metric (the Chen–LeBrun–Weber metric). We compare our approximation to one given by Bunch and Donaldson and compute various geometric quantities. In particular, we demonstrate a small eigenvalue of the scalar Laplacian of the Einstein metric that gives numerical evidence that the Einstein metric is conformally unstable under Ricci flow.
, which is conformal to an Einstein metric (the Chen–LeBrun–Weber metric). We compare our approximation to one given by Bunch and Donaldson and compute various geometric quantities. In particular, we demonstrate a small eigenvalue of the scalar Laplacian of the Einstein metric that gives numerical evidence that the Einstein metric is conformally unstable under Ricci flow.
- Type
- Research Article
- Information
- Proceedings of the Edinburgh Mathematical Society , Volume 60 , Issue 4 , November 2017 , pp. 893 - 910
- Copyright
- Copyright © Edinburgh Mathematical Society 2017




