Hostname: page-component-7479d7b7d-pfhbr Total loading time: 0 Render date: 2024-07-10T17:23:28.359Z Has data issue: false hasContentIssue false
  • English
  • Français

Hausdorff Dimension of Sets of Escaping Points and Escaping Parameters for Elliptic Functions

Part of: Complex dynamical systems Entire and meromorphic functions, and related topics

Published online by Cambridge University Press:  30 December 2015

Piotr Gałązka  and
Janina Kotus
Piotr Gałązka
Affiliation:
Faculty of Mathematics and Information Science, Warsaw University of Technology, ul. Koszykowa 75, 00-662 Warszawa, Poland (p.galazka@mini.pw.edu.pl; j.kotus@impan.pl)
Janina Kotus
Affiliation:
Faculty of Mathematics and Information Science, Warsaw University of Technology, ul. Koszykowa 75, 00-662 Warszawa, Poland (p.galazka@mini.pw.edu.pl; j.kotus@impan.pl)
Get access Rights & Permissions [Opens in a new window]

Abstract

Let 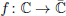be a non-constant elliptic function. We prove that the Hausdorff dimension of the escaping set of f equals 2q/(q+1), where q is the maximal multiplicity of poles of f. We also consider the escaping parameters in the family fβ = βf, i.e. the parameters β for which the orbit of one critical value of fβ escapes to infinity. Under additional assumptions on f we prove that the Hausdorff dimension of the set of escaping parameters ε in the family fβ is greater than or equal to the Hausdorff dimension of the escaping set in the dynamical space. This demonstrates an analogy between the dynamical plane and the parameter plane in the class of transcendental meromorphic functions.

Keywords

meromorphic functionsJulia setcritical valuesescaping setescaping parametersHausdorff dimension

MSC classification

Secondary: 37F10: Polynomials; rational maps; entire and meromorphic functions 30D05: Functional equations in the complex domain, iteration and composition of analytic functions
Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 59 , Issue 3 , August 2016 , pp. 671 - 690
Copyright
Copyright © Edinburgh Mathematical Society 2015 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1. Baránski, K., Hausdorff dimension of hairs and ends for entire maps of finite order, Math. Proc. Camb. Phil. Soc. 145 (2008), 719–737.Google Scholar
2. Bergweiler, W., On the packing dimension of the Julia set and the escaping set of an entire function, Israel J. Math. 192 (2012), 449–472.Google Scholar
3. Bergweiler, W. and Kotus, J., On the Hausdorff dimension of the escaping set of certain meromorphic functions, Trans. Am. Math. Soc. 364 (2012), 5369–5394.Google Scholar
4. Domínguez, P., Dynamics of transcendental meromorphic functions, Annales Acad. Sci. Fenn. Math. 23 (1998), 225–250.Google Scholar
5. Hawkins, J. and Koss, L., Ergodic properties and Julia sets of Weierstrass elliptic functions, Monatsh. Math. 137(4) (2002), 273–300.Google Scholar
6. Hawkins, J. and Koss, L., Connectivity properties of Julia sets of Weierstrass elliptic functions, Topol. Applic. 152 (2005), 107–137.CrossRefGoogle Scholar
7. Karpińska, B., Area and Hausdorff dimension of the set of accessible points of the Julia sets of ƛe z and ƛ sin z , Fund. Math. 159 (1999), 269–287.Google Scholar
8. Kotus, J., On the Hausdorff dimension of Julia sets of meromorphic functions, II, Bull. Soc. Math. France 123 (1995), 33–46.Google Scholar
9. Kotus, J.and Urbański, M., Hausdorff dimension and Hausdorff measures of Julia sets of elliptic functions, Bull. Lond. Math. Soc. 35 (2003), 269–275.Google Scholar
10. Kotus, J. and Urbański, M., Geometry and ergodic theory of non-recurrent elliptic functions, J. Analysis Math. 93 (2004), 35–102.Google Scholar
11. Kotus, J. and Urbański, M., Ergodic theory, geometric measure theory and the dynamics of elliptic functions, Preprint (available at http://www.mini.pw.edu.pl/~kotus/www/pdf/NCP_2013.11.22.pdf).Google Scholar
12. McMullen, C., Area and Hausdorff dimension of Julia sets of entire functions, Trans. Am. Math. Soc. 300 (1987), 329–342.Google Scholar
13. Qiu, W., Hausdoff Dimension of the M-Set of ƛ exp(z), Acta Math. Sinica 10 (1994), 362–368.Google Scholar
14. Rippon, P. J. and Stallard, G. M., Escaping points of meromorphic functions with a finite number of poles, J. Analysis Math. 96 (2005), 225–245.Google Scholar
15. Rippon, P. J. and Stallard, G. M., Fast escaping points of entire functions, Proc. Lond. Math. Soc. 105 (2012), 787–820.Google Scholar