Hostname: page-component-848d4c4894-cjp7w Total loading time: 0 Render date: 2024-06-17T00:13:16.670Z Has data issue: false hasContentIssue false
  • English
  • Français

A generalization of centralizer near-rings

Published online by Cambridge University Press:  20 January 2009

Kirby C. Smith
Kirby C. Smith
Affiliation:
Department of MathematicsTexas A&M UniversityCollege StationTexas 77843-3368
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let G be a group with identity 0 and let 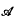be a group of automorphisms of G. The centralizer near-ring determined by G and 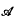is the set 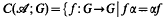for all α∈ 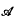and f(0)=0}, forming a near-ring under function addition and function composition. This class of nea-rings has been extensively studied (for example see [1], [2], [5] and [6]) and it is known that every finite simple near-ring with identity which is not a ring is isomorphic to C(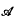;G) for a suitable pair (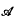,G) see [6] page 131, Corollary 4.59 and Theorem 4.60.

Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 28 , Issue 2 , June 1985 , pp. 159 - 165
Copyright
Copyright © Edinburgh Mathematical Society 1985

References

REFERENCES

1.Maxson, C. J., and Smith, K. C., The centralizer of a set of group automorphisms, Comm. in Algebra 8 (1980), 211–230.CrossRefGoogle Scholar
2.Maxson, C. J., and Smith, K. C., Centralizer near-ring representations, Proc. Edin. Math. Soc. 25 (1982), 145–153.Google Scholar
3.Maxson, C. J., and Smith, K. C., Centralizer near-rings: left ideals and 0-primitivity, Proc. Royal Irish Acad. 81A (1981), 187–199.Google Scholar
4.Maxson, C. J., Pettet, M. R. and Smith, K. C., On semisimple rings that are centralizer nearrings, Pacific J. of Math. 101 (1982), 451–461.Google Scholar
5.Meldrum, J. D. P. and Zeller, M., Simplicity of near-rings of mappings, Proc. Roy. Soc. Edinburgh 90A (1981), 185–193.CrossRefGoogle Scholar
6.Pilz, G., Near-rings, revised edition (North-Holland, 1983).Google Scholar
7.Smith, K. C., The lattice of left ideals in a centralizer near-ring is distributive, Proc. Amer. Math. Soc. 85 (1982), 313–317.CrossRefGoogle Scholar