Hostname: page-component-76fb5796d-qxdb6 Total loading time: 0 Render date: 2024-04-27T03:44:16.533Z Has data issue: false hasContentIssue false
  • English
  • Français

Fusion systems and group actions with abelian isotropy subgroups

Part of: Representation theory of groups

Published online by Cambridge University Press:  10 July 2013

Özgün Ünlü  and
Ergün Yalçin
Özgün Ünlü
Affiliation:
Department of Mathematics, Bilkent University, Ankara 06800, Turkey (unluo@fen.bilkent.edu.tr; yalcine@fen.bilkent.edu.tr)
Ergün Yalçin
Affiliation:
Department of Mathematics, Bilkent University, Ankara 06800, Turkey (unluo@fen.bilkent.edu.tr; yalcine@fen.bilkent.edu.tr)
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We prove that if a finite group G acts smoothly on a manifold M such that all the isotropy subgroups are abelian groups with rank ≤ k, then G acts freely and smoothly on M × 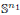× … × 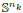for some positive integers n1, …, nk. We construct these actions using a recursive method, introduced in an earlier paper, that involves abstract fusion systems on finite groups. As another application of this method, we prove that every finite solvable group acts freely and smoothly on some product of spheres, with trivial action on homology.

Keywords

fusion systemsfree actions on manifoldsproducts of spheres

MSC classification

Secondary: 57S25: Groups acting on specific manifolds 20D20: Sylow subgroups, Sylow properties, $pi$-groups, $pi$-structure
Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 56 , Issue 3 , October 2013 , pp. 873 - 886
Copyright
Copyright © Edinburgh Mathematical Society 2013 

References

1.Adem, A., Davis, J. F. and Ünlü, Ö., Fixity and free group actions on products of spheres, Comment. Math. Helv. 79 (2004), 758–778.CrossRefGoogle Scholar
2.Bouc, S., Biset functors for finite groups, Lecture Notes in Mathematics, Volume 1990 (Springer, 2010).Google Scholar
3.Heller, A., A note on spaces with operators, Illinois J. Math. 3 (1959), 98–100.CrossRefGoogle Scholar
4.Holm, P., Microbundles and Thom classes, Bull. Am. Math. Soc. 72 (1966), 549–554.CrossRefGoogle Scholar
5.Klaus, M., Constructing free actions of p-groups on products of spheres, Alg. Geom. Top. 11 (2011), 3065–3084.CrossRefGoogle Scholar
6.Lück, W. and Oliver, R., The completion theorem in K-theory for proper actions of a discrete group, Topology 40 (2001), 585–616.CrossRefGoogle Scholar
7.Madsen, I., Thomas, C. B. and Wall, C. T. C., The topological spherical space form problem, II, Topology 15 (1978), 375–382.CrossRefGoogle Scholar
8.Milnor, J., Groups which act on without fixed points, Am. J. Math. 79 (1957), 623–630.CrossRefGoogle Scholar
9.Oliver, R., Free compact group actions on products of spheres, in Algebraic topology, Lecture Notes in Mathematics, Volume 763, pp. 539–548 (Springer, 1979).Google Scholar
10.Park, S., Realizing a fusion system by a single group, Arch. Math. 94 (2010), 405–410.CrossRefGoogle Scholar
11.Ray, U., Free linear actions of finite groups on products of spheres, J. Alg. 147 (1992), 456–490.CrossRefGoogle Scholar
12.Smith, P. A., Permutable periodic transformations, Proc. Natl Acad. Sci. USA 30 (1944), 105–108.CrossRefGoogle ScholarPubMed
13.Spanier, E. H., Algebraic topology (Springer, 1966).Google Scholar
14.Ünlü, Ö. and Yalçin, E., Quasilinear actions on products of spheres, Bull. Lond. Math. Soc. 42 (2010), 981–990.CrossRefGoogle Scholar
15.Ünlü, Ö. and Yalçin, E., Fusion systems and constructing free actions on products of spheres, Math. Z. 270 (2012), 939–959.CrossRefGoogle Scholar