Hostname: page-component-848d4c4894-nr4z6 Total loading time: 0 Render date: 2024-06-04T21:47:02.814Z Has data issue: false hasContentIssue false
  • English
  • Français

A Determinantal Expansion for a Glass of Definite Integral1. Part 1

Published online by Cambridge University Press:  20 January 2009

L. R. Shenton
L. R. Shenton
Affiliation:
College of Technology, Manchester, 1.
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

1. Let w(x) be a non-negative weight function for the finite interval (a, b) such that exists and is positive, and let Tr(x), r = 0, 1, 2,…be the corresponding orthonormal system of polynomials. Then if F(x) is continuous on (a, b) and has “Fourier” coefficients

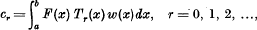
Parseval's formula gives

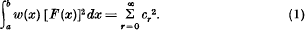
Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 9 , Issue 1 , October 1953 , pp. 44 - 52
Copyright
Copyright © Edinburgh Mathematical Society 1953

References

2 See for example Jackson, D., Fourier Series and Orthogonal Polynomials (Carus Math. Mon., 1941), Ch. II, and p. 228Google Scholar, or Szegö, G., Orthogonal Polynomials (New York, 1939), Ch. III.CrossRefGoogle Scholar

1 See Szegö, , loe. cit., Ch. II.Google Scholar

2 Muir, , Theory of Determinants, Pts. I and II (London, 1906)Google Scholar, or Aitken, A. C.. Determinants and Matrices (Edinburgh, 1946).Google Scholar

1 See for example Wall, H. S., Continued Fractions (New York, 1948), Ch. XIII onwardsGoogle Scholar, or Perron, O., Die Lehre von den Kettenbrüchen (Leipzig, 1913), Ch. 9.Google Scholar

2 Muir, , Theory of Determinants, Vol. III (London, 1920).Google Scholar

3 Kogers, L. J., "Asymptotic series as convergent continued fractions", Proc. London Math. Soc. (2), 4 (1905–1906).Google Scholar

1 Aitken, , loc. cit.Google Scholar

2 Kowalewski, G., Einführung in die Determinantentheorie (Leipzig, 1925), 224.Google Scholar

1 Bateman, H., Partial Differential Equations (New York, 1944), 392.Google Scholar

1 Burchnall, J. L., Quart. Journ. Math., Oxford, 2nd Series 3, 10 (1952), 151–157.CrossRefGoogle Scholar