Hostname: page-component-848d4c4894-75dct Total loading time: 0 Render date: 2024-05-25T10:18:24.775Z Has data issue: false hasContentIssue false
  • English
  • Français

An Interpolation Series for Integral Functions

Published online by Cambridge University Press:  20 January 2009

Sheila Scott Macintyre
Sheila Scott Macintyre
Affiliation:
The University, Aberdeen.
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

1. The Gontcharoff interpolation series

where

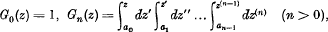
has been studied in various special cases. For example, if an = a0 (all n), (1.0) reduces to the Taylor expansion of F(z). If an = (−1)n, J. M. Whittaker showed that the series (1.0) converges to F(z) provided F(z) is an integral function whose maximum modulus satisfies

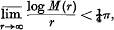
the constant ¼π being the “best possible”. In the case |an| ≤ 1, I have shown that the series converges to F(z) provided F(z) is an integral function whose maximum modulus satisfies

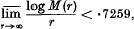
and that while ·7259 is not the “best possible” constant here, it cannot be replaced by a number as great as ·7378.

Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 9 , Issue 1 , October 1953 , pp. 1 - 6
Copyright
Copyright © Edinburgh Mathematical Society 1953

References

REFERENCES

Boas, R. P. Jr, “Functions of exponential type II,” Duke Math. Journal, 11 (1944), 17–22.Google Scholar
Boas, R. P. Jr, “Functions of exponential type IV,” Duke Math. Journal, 11 (1944), 799.Google Scholar
Macintyre, Sheila Scott, “An upper bound for the Whittaker constant W,” Journal London Math. Soc., 32 (1947), 305–311.CrossRefGoogle Scholar
Macintyre, Sheila Scott, “On the zeros of successive derivatives of integral functions,” Trans. American Math. Soc., 62 (1949), 241–251.CrossRefGoogle Scholar
Whittaker, J. M., “Lidstone's series and two-point expansions of analytic functions,” Proc. London Math. Soc. (2), 36 (1932), 451–469.Google Scholar
Whittaker, J. M., Interpolatory Function Theory (Cambridge, 1935).Google Scholar