Hostname: page-component-848d4c4894-jbqgn Total loading time: 0 Render date: 2024-06-15T18:32:51.034Z Has data issue: false hasContentIssue false
  • English
  • Français

An algebraic link concordance group for (p, 2p−1)-links in S2p+1

Published online by Cambridge University Press:  20 January 2009

Pat Gilmer  and
Charles Livingston
Pat Gilmer
Affiliation:
Mathematics DepartmentLouisiana State UniversityBaton Rouge, LA 70803
Charles Livingston
Affiliation:
Mathematics DepartmentIndiana UniversityBloomington, IN 47405
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

A concordance classification of links of 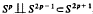, p < 1, is given in terms of an algebraically defined group, Φ±, which is closely related to Levine's algebraic knot concordance group. For p=1,Φ_ captures certain obstructions to two component links in S3 being concordant to boundary links, the generalized Sato-Levine invariants defined by Cochran. As a result, purely algebraic proofs of properties of these invariants are derived.

Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 34 , Issue 3 , October 1991 , pp. 455 - 462
Copyright
Copyright © Edinburgh Mathematical Society 1991

References

REFERENCES

1.Casson, A. and Gordon, C. McA., On slice knots in dimension three, Proc. Sympos. Pure Math. 30 (1978), 39–53.Google Scholar
2.Cochran, T., Geometric invariants of link cobordism, Comment. Math. Helv. 60 (1985), 291–311.CrossRefGoogle Scholar
3.Gilmer, P. and Livingston, C., The Casson-Gordon invariant and link concordance, preprint.Google Scholar
4.Hacon, D., Embeddings of S p in S 1 × Sq in the metastable range, Topology 7 (1968), 1–10.CrossRefGoogle Scholar
5.Hacon, D. and Mio, W., Self-linking Invariants of Embeddings in the Metastable Range (Informes de Matematica do IMPA, Serie A-067-March, 1987).Google Scholar
6.Hirsch, M., Embeddings and compressions of polyhedra and smooth manifolds, Topology 4 (1966), 361–369.Google Scholar
7.Jin, G. T., On Kojima's η function of links, in Differential Topology, Proceedings, Siegen 1987 (ed. Koschorke, U., Springer Lecture Notes 1350).Google Scholar
8.Kervaire, M., Knot cobordism in codimension two, in Manifolds—Amsterdam, 1970 (Springer Lecture Notes 197).Google Scholar
9.Kojima, S. and Yamasaki, M., Some new invariants of links, Invent. Math. 54 (1979), 213–228.CrossRefGoogle Scholar
10.Levine, J., Knot cobordism groups in codimension two, Comment. Math. Helv. 44 (1969), 229–244.CrossRefGoogle Scholar
11.Levine, J., Invariants of knot cobordism, Invent. Math. 8 (1969), 98–110.CrossRefGoogle Scholar
12.Sato, N., Cobordisms of semi-boundary links, Topology Appl. 18 (1984), 225–234.CrossRefGoogle Scholar
13.Stoltzfus, N., Unraveling the integral knot concordance group, Mem. Amer. Math. Soc. 192 (1977).Google Scholar