Hostname: page-component-77c89778f8-gvh9x Total loading time: 0 Render date: 2024-07-17T10:51:13.331Z Has data issue: false hasContentIssue false
  • English
  • Français

On simultaneous rational approximation to a p-adic number and its integral powers, II

Part of: Diophantine approximation, transcendental number theory

Published online by Cambridge University Press:  07 May 2021

Dzmitry Badziahin ,
Yann Bugeaud  and
Johannes Schleischitz
Dzmitry Badziahin
Affiliation:
School of Mathematics and Statistics, The University of Sydney, Camperdown, NSW2006, Australia (dzmitry.badziahin@sydney.edu.au)
Yann Bugeaud
Affiliation:
Université de Strasbourg, Mathématiques, 7, rue René Descartes, Strasbourg67084, France (bugeaud@math.unistra.fr)
Johannes Schleischitz
Affiliation:
Middle East Technical University, Northern Cyprus Campus, Kalkanli, Güzelyurt, Turkey (johannes@metu.edu.tr)
Get access Rights & Permissions [Opens in a new window]

Abstract

Let $p$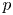 be a prime number. For a positive integer $n$ 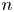and a real number $\xi$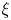, let $\lambda _n (\xi )$ denote the supremum of the real numbers $\lambda$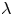 for which there are infinitely many integer tuples $(x_0, x_1, \ldots , x_n)$ 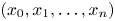such that $| x_0 \xi - x_1|_p, \ldots , | x_0 \xi ^{n} - x_n|_p$ 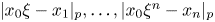are all less than $X^{-\lambda - 1}$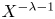, where $X$ 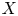is the maximum of $|x_0|, |x_1|, \ldots , |x_n|$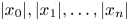. We establish new results on the Hausdorff dimension of the set of real numbers $\xi$ 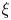for which $\lambda _n (\xi )$ is equal to (or greater than or equal to) a given value.

Keywords

simultaneous approximationtransference theorem

MSC classification

Primary: 11J13: Simultaneous homogeneous approximation, linear forms
Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 64 , Issue 2 , May 2021 , pp. 317 - 337
Check for updates
Copyright
Copyright © The Author(s), 2021. Published by Cambridge University Press on Behalf of The Edinburgh Mathematical Society

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Badziahin, D. and Bugeaud, Y., On simultaneous rational approximation to a real number and its integral powers II, N. Y. J. Math. 26 (2020), 362–377.Google Scholar
Beresnevich, V., Dickinson, D. and Velani, S., Diophantine approximation on planar curves and the distribution of rational points. With an Appendix II by R. C. Vaughan, Ann. Math. (2) 166(2) (2007), 367–426.10.4007/annals.2007.166.367CrossRefGoogle Scholar
Bernik, V. I. and Dodson, M. M., Metric Diophantine approximation on manifolds, Cambridge Tracts in Mathematics, Volume 137 (Cambridge University Press, 1999).CrossRefGoogle Scholar
Bernik, V. I. and Morotskaya, I. L., Diophantine approximations in ${{\mathbb {Q}}}_p$ and Hausdorff dimension, Vestsi Akad. Navuk BSSR Ser. Fiz.-Mat. Navuk 3 (1986), 3–9, 123 (in Russian).Google Scholar
Bombieri, E. and Gubler, W., Heights in diophantine geometry (New Mathematical Monographs, Volume 4 (Cambridge University Press, 2006).Google Scholar
Budarina, N., Bugeaud, Y., Dickinson, D. and O'Donnell, H., On simultaneous rational approximation to a $p$-adic number and its integral powers, Proc. Edinb. Math. Soc. 54 (2011), 599–612.Google Scholar
Bugeaud, Y., Approximation by algebraic numbers, Cambridge Tracts in Mathematics (Cambridge University Press, 2004).10.1017/CBO9780511542886CrossRefGoogle Scholar
Cassels, J. W. S., An introduction to the geometry of numbers (Springer Verlag, 1959).CrossRefGoogle Scholar
Champagne, J. and Roy, D., A transference inequality for rational approximation to points in geometric progression, Hardy–Ramanujan J. 42 (2019), 70–72.Google Scholar
Davenport, H. and Schmidt, W. M., Approximation to real numbers by algebraic integers, Acta Arith. 15 (1969), 393–416.CrossRefGoogle Scholar
Jarník, V., Über einen $p$-adischen Übertragungssatz, Monatsh. Math. Phys. 48 (1939), 277–287.10.1007/BF01696184CrossRefGoogle Scholar
Jarník, V., Sur les approximations diophantiques des nombres $p$-adiques, Rev. Ci. (Lima) 47 (1945), 489–505.Google Scholar
Laurent, M., Simultaneous rational approximation to the successive powers of a real number, Indag. Math. 11 (2003), 45–53.CrossRefGoogle Scholar
Lutz, É., Sur les approximations diophantiennes linéaires p-adiques, Actualités Sci. Ind., Volume 1224, 106 p. (Paris, Hermann & Cie, 1955).Google Scholar
Mahler, K., Über Diophantische Approximationen in Gebiete der $p$-adische Zahlen, Jahresbericht d. Deutschen Math. Verein. 44 (1934), 250–255.Google Scholar
Mahler, K., Über eine Klassen-einteilung der $p$-adischen Zahlen, Math. Leiden 3 (1935), 177–185.Google Scholar
Morotskaya, I. L., Hausdorff dimension and Diophantine approximations in ${{\mathbb {Q}}}_p$, Dokl. Akad. Nauk BSSR 31 (1987), 597–600, 668 (in Russian).Google Scholar
Schleischitz, J., On the spectrum of Diophantine approximation constants, Mathematika 62 (2016), 79–100.CrossRefGoogle Scholar
Schleischitz, J., On uniform approximation to successive powers of a real number, Indag. Math. 28 (2017), 406–423.10.1016/j.indag.2016.11.001CrossRefGoogle Scholar
Sprindžuk, V. G., Mahler's problem in metric number theory (American Mathematical Society, 1969).Google Scholar
Teulié, O., Approximation d'un nombre $p$-adique par des nombres algébriques, Acta Arith. 102 (2002), 137–155.10.4064/aa102-2-3CrossRefGoogle Scholar
Vaughan, R. C. and Velani, S., Diophantine approximation on planar curves: the convergence theory, Invent. Math. 166(1) (2006), 103–124.CrossRefGoogle Scholar