No CrossRef data available.
Article contents
Coprime subdegrees of twisted wreath permutation groups
Published online by Cambridge University Press: 28 June 2019
Abstract
Dolfi, Guralnick, Praeger and Spiga asked whether there exist infinitely many primitive groups of twisted wreath type with non-trivial coprime subdegrees. Here, we settle this question in the affirmative. We construct infinite families of primitive twisted wreath permutation groups with non-trivial coprime subdegrees. In particular, we define a primitive twisted wreath group G(m, q) constructed from the non-abelian simple group PSL(2, q) and a primitive permutation group of diagonal type with socle PSL(2, q)m, and determine many subdegrees for this group. A consequence is that we determine all values of m and q for which G(m, q) has non-trivial coprime subdegrees. In the case where m = 2 and 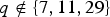 $q\notin \{7,11,29\}$, we obtain a full classification of all pairs of non-trivial coprime subdegrees.
$q\notin \{7,11,29\}$, we obtain a full classification of all pairs of non-trivial coprime subdegrees.
MSC classification
- Type
- Research Article
- Information
- Proceedings of the Edinburgh Mathematical Society , Volume 62 , Issue 4 , November 2019 , pp. 1137 - 1162
- Copyright
- Copyright © Edinburgh Mathematical Society 2019




