No CrossRef data available.
Article contents
Alternative statistical methods in the study of growth and body composition of animals
Published online by Cambridge University Press: 05 November 2021
Extract
Body composition of animals may change (a) in response to treatments or (b) as they grow older. Studies on (a) generally model each component of composition separately, without the constraint that predicted components sum to 1 (e.g. Keane et al 1990). Allometric regression is widely used in studies of growth and differentiation (change in component proportions). This frequently involves estimating the parameters of a linear relation
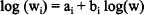 between the logarithm of weight of an organ or part (Wi) and the logarithm of the weight of the whole animal (w). Sometimes the relation is between an organ and a part of the animal that contains the organ as a subcomponent. A similar difficulty as in (a) arises here also. The allometric regression equations can be recast to give predictive models for the composition of the animal at different weights. In this form the model is
between the logarithm of weight of an organ or part (Wi) and the logarithm of the weight of the whole animal (w). Sometimes the relation is between an organ and a part of the animal that contains the organ as a subcomponent. A similar difficulty as in (a) arises here also. The allometric regression equations can be recast to give predictive models for the composition of the animal at different weights. In this form the model is
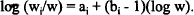
- Type
- Programme
- Information
- Copyright
- Copyright © The British Society of Animal Science 1998




