Article contents
Ordering and aging properties of systems with dependent components governed by the Archimedean copula
Published online by Cambridge University Press: 17 September 2021
Abstract
Copula is one of the widely used techniques to describe the dependency structure between components of a system. Among all existing copulas, the family of Archimedean copulas is the popular one due to its wide range of capturing the dependency structures. In this paper, we consider the systems that are formed by dependent and identically distributed components, where the dependency structures are described by Archimedean copulas. We study some stochastic comparisons results for series, parallel, and general 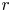 $r$-out-of-
$r$-out-of-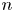 $n$ systems. Furthermore, we investigate whether a system of used components performs better than a used system with respect to different stochastic orders. Furthermore, some aging properties of these systems have been studied. Finally, some numerical examples are given to illustrate the proposed results.
$n$ systems. Furthermore, we investigate whether a system of used components performs better than a used system with respect to different stochastic orders. Furthermore, some aging properties of these systems have been studied. Finally, some numerical examples are given to illustrate the proposed results.
MSC classification
- Type
- Research Article
- Information
- Probability in the Engineering and Informational Sciences , Volume 37 , Issue 1 , January 2023 , pp. 1 - 28
- Copyright
- Copyright © The Author(s), 2021. Published by Cambridge University Press
References
- 4
- Cited by




