Research Article
Riemannian Manifolds with Discontinuous Metrics and the Dirichlet Integral
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. 1-48
-
- Article
-
- You have access
- Export citation
On Holomorphic Maps into a Taut Complex Space
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. 49-61
-
- Article
-
- You have access
- Export citation
Gaussian Sample Functions: Uniform Dimension and Hölder Conditions Nowhere
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. 63-86
-
- Article
-
- You have access
- Export citation
On Nilpotent Groups of Algebra Automorphisms
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. 87-95
-
- Article
-
- You have access
- Export citation
Ramification Theory for Extensions of Degree p. II
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. 97-109
-
- Article
-
- You have access
- Export citation
Tangential Boundary Properties of Arbitrary Functions in the Unit Disc
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. 111-120
-
- Article
-
- You have access
- Export citation
Linear Imbeddings of Self-Dual Homogeneous Cones
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. 121-145
-
- Article
-
- You have access
- Export citation
On Ramification Theory in Projective Orders, II
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. 147-153
-
- Article
-
- You have access
- Export citation
On Abstract Wiener Measure*
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. 155-160
-
- Article
-
- You have access
- Export citation
Remarks on Kähler-Einstein Manifolds
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. 161-173
-
- Article
-
- You have access
- Export citation
Front Matter
NMJ volume 46 Cover and Front matter
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. f1-f4
-
- Article
-
- You have access
- Export citation
Back Matter
NMJ volume 46 Cover and Back matter
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. b1-b2
-
- Article
-
- You have access
- Export citation

 , is used for the variation with Euler-Lagrange equation
, is used for the variation with Euler-Lagrange equation
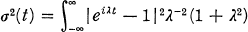 dH(λ), for some bounded monotone
dH(λ), for some bounded monotone 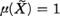 and
and 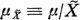 is the σ-extension of the canonical Gaussian cylinder measure
is the σ-extension of the canonical Gaussian cylinder measure  of a real separable Hilbert space
of a real separable Hilbert space 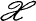 such that the norm
such that the norm  is contiunous on
is contiunous on  The main purpose of this note is to prove that
The main purpose of this note is to prove that