Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Schiff, Joel L.
1972.
A note on the space of Dirichlet-finite solutions of $\Delta u=Pu$ on a Riemann surface.
Hiroshima Mathematical Journal,
Vol. 2,
Issue. 2,
Nakai, Mitsuru
1973.
Order Comparisons on Canonical Isomorphisms.
Nagoya Mathematical Journal,
Vol. 50,
Issue. ,
p.
67.
Nakai, Mitsuru
1973.
Uniform densities on hyperbolic Riemannl surfaces.
Nagoya Mathematical Journal,
Vol. 51,
Issue. ,
p.
1.
Maeda, Fumi Yuki
1974.
Dirichlet integrals of functions on a self-adjoint harmonic space.
Hiroshima Mathematical Journal,
Vol. 4,
Issue. 3,
Maeda, Fumi-Yuki
1978.
Classification theory for nonlinear functional-harmonic spaces.
Hiroshima Mathematical Journal,
Vol. 8,
Issue. 2,
Glasner, Moses
and
Nakai, Mitsuru
1981.
Images of reduction operators.
Archive for Rational Mechanics and Analysis,
Vol. 75,
Issue. 4,
p.
387.
Tanaka, Hiroshi
1990.
Harmonic boundaries of Riemannian manifolds.
Nonlinear Analysis: Theory, Methods & Applications,
Vol. 14,
Issue. 1,
p.
55.
Nakai, Mitsuru
1992.
Riemannian manifolds with connected Royden harmonic boundaries.
Duke Mathematical Journal,
Vol. 67,
Issue. 3,
Nakai, Mitsuru
1994.
Existence of Dirichlet finite harmonic measures on Euclidean balls.
Nagoya Mathematical Journal,
Vol. 133,
Issue. ,
p.
85.
Maeda, Fumi-Yuki
and
Ono, Takayori
2000.
Properties of harmonic boundary in nonlinear potential theory.
Hiroshima Mathematical Journal,
Vol. 30,
Issue. 3,
Hua, Bobo
Liu, Shiping
and
Xia, Chao
2017.
Liouville theorems for f-harmonic maps into
Hadamard spaces.
Pacific Journal of Mathematics,
Vol. 290,
Issue. 2,
p.
381.




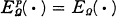 , is used for the variation with Euler-Lagrange equation
, is used for the variation with Euler-Lagrange equation
