Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Robbiano, Lorenzo
1984.
Complete Intersections.
Vol. 1092,
Issue. ,
p.
62.
Wahl, Jonathan M.
1987.
The Jacobian algebra of a graded Gorenstein singularity.
Duke Mathematical Journal,
Vol. 55,
Issue. 4,
SAITO, Kyoji
1988.
Algebraic Geometry and Commutative Algebra.
p.
517.
WATANABE, Kei-ichi
1988.
Algebraic Geometry and Commutative Algebra.
p.
791.
Wahl, Jonathan
1988.
Deformations of quasi-homogeneous surface singularities.
Mathematische Annalen,
Vol. 280,
Issue. 1,
p.
105.
Carbonne, P.
1989.
Séminaire d’Algèbre Paul Dubreil et Marie-Paul Malliavin.
Vol. 1404,
Issue. ,
p.
174.
Levasseur, Thierry
1989.
Séminaire d’Algèbre Paul Dubreil et Marie-Paul Malliavin.
Vol. 1404,
Issue. ,
p.
269.
Tomaru, Tadashi
1989.
On a class of normal surface singularities determined by weierstrass points on algebraic curves.
Communications in Algebra,
Vol. 17,
Issue. 3,
p.
703.
Hidaka, Fumio
and
Tomari, Masataka
1989.
On singularities arising from the contraction op the minimal section of a ruled surface.
Manuscripta Mathematica,
Vol. 65,
Issue. 3,
p.
329.
Watanabe, Kei-ichi
1991.
F-regular and F-pure normal graded rings.
Journal of Pure and Applied Algebra,
Vol. 71,
Issue. 2-3,
p.
341.
Tomari, Masataka
1991.
The canonical filtration of higher dimensional purely elliptic singularity of a special type.
Inventiones mathematicae,
Vol. 104,
Issue. 1,
p.
497.
Noma, Atsushi
1991.
Gorenstein toric singularities and convex polytopes.
Tohoku Mathematical Journal,
Vol. 43,
Issue. 4,
Tomaru, Tadashi
1992.
Cyclic quotients of 2-dimensional quasi-homogeneous hypersurface singularities.
Mathematische Zeitschrift,
Vol. 210,
Issue. 1,
p.
225.
Tomari, Masataka
and
Watanabe, Kei-ichi
1992.
NormalZ r-graded rings and normal cyclic covers.
Manuscripta Mathematica,
Vol. 76,
Issue. 1,
p.
325.
Tomaru, Tadashi
1994.
On numerically Gorenstein quasi-simple elliptic singularities with 𝐶*-action.
Proceedings of the American Mathematical Society,
Vol. 120,
Issue. 1,
p.
67.
Hara, Nobuo
and
Watanabe, Kei-ichi
1996.
The injectivity of Frobenius acting on cohomology and local cohomology modules.
Manuscripta Mathematica,
Vol. 90,
Issue. 1,
p.
301.
Drewes, R.
and
Stevens, J.
1996.
Deformations of cones over canonical trigonal curves.
Abhandlungen aus dem Mathematischen Seminar der Universität Hamburg,
Vol. 66,
Issue. 1,
p.
289.
Watanabe, Kei-ichi
1997.
F-rationality of certain Rees algebras and counterexamples to “Boutot's Theorem” for F-rational rings.
Journal of Pure and Applied Algebra,
Vol. 122,
Issue. 3,
p.
323.
Küchle, Oliver
1997.
SOME REMARKS AID PROBLEMS CONCERNING THE GEOGRAPHY OF FANO 4-FOLDS OF INDEX AND PICARDNUMBER ONE.
Quaestiones Mathematicae,
Vol. 20,
Issue. 1,
p.
45.
Singh, Anurag K.
2000.
Veronese subrings and tight closure.
Pacific Journal of Mathematics,
Vol. 192,
Issue. 2,
p.
399.
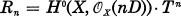 for every n ≧ 0.(See (1.1) for the definition of
for every n ≧ 0.(See (1.1) for the definition of