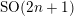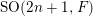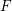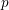Introduction
Cet article est la suite de [Reference Waldspurger11], dont on utilise les définitions et notations. Ces dernières sont rappelées dans l’index à la fin de l’article. Le corps de base
![]() $F$
est local, non archimédien et de caractéristique nulle. On note
$F$
est local, non archimédien et de caractéristique nulle. On note
![]() $p$
sa caractéristique résiduelle. Un entier
$p$
sa caractéristique résiduelle. Un entier
![]() $n\geqslant 1$
est fixé pour tout l’article. On suppose que
$n\geqslant 1$
est fixé pour tout l’article. On suppose que
![]() $p\geqslant 6n+4$
. On s’intéresse aux groupes
$p\geqslant 6n+4$
. On s’intéresse aux groupes
![]() $G_{\operatorname{iso}}$
et
$G_{\operatorname{iso}}$
et
![]() $G_{\operatorname{an}}$
définis en [Reference Waldspurger11] 1.1. Le groupe
$G_{\operatorname{an}}$
définis en [Reference Waldspurger11] 1.1. Le groupe
![]() $G_{\operatorname{iso}}$
est le groupe spécial orthogonal d’un espace
$G_{\operatorname{iso}}$
est le groupe spécial orthogonal d’un espace
![]() $V_{\operatorname{iso}}$
de dimension
$V_{\operatorname{iso}}$
de dimension
![]() $2n+1$
sur
$2n+1$
sur
![]() $F$
muni d’une forme quadratique
$F$
muni d’une forme quadratique
![]() $Q_{\operatorname{iso}}$
et
$Q_{\operatorname{iso}}$
et
![]() $G_{\operatorname{an}}$
est le groupe spécial orthogonal d’un espace
$G_{\operatorname{an}}$
est le groupe spécial orthogonal d’un espace
![]() $V_{\operatorname{an}}$
de dimension
$V_{\operatorname{an}}$
de dimension
![]() $2n+1$
sur
$2n+1$
sur
![]() $F$
muni d’une forme quadratique
$F$
muni d’une forme quadratique
![]() $Q_{\operatorname{an}}$
. Le groupe
$Q_{\operatorname{an}}$
. Le groupe
![]() $G_{\operatorname{iso}}$
est déployé et
$G_{\operatorname{iso}}$
est déployé et
![]() $G_{\operatorname{an}}$
en est la forme intérieure non déployée. Pour un indice
$G_{\operatorname{an}}$
en est la forme intérieure non déployée. Pour un indice
![]() $\sharp =\operatorname{iso}$
ou
$\sharp =\operatorname{iso}$
ou
![]() $\operatorname{an}$
, on note
$\operatorname{an}$
, on note
![]() $\operatorname{Irr}_{\operatorname{tunip},\sharp }$
l’ensemble des classes d’isomorphismes de représentations admissibles irréductibles de
$\operatorname{Irr}_{\operatorname{tunip},\sharp }$
l’ensemble des classes d’isomorphismes de représentations admissibles irréductibles de
![]() $G_{\sharp }(F)$
qui sont tempérées et de réduction unipotente, cf. [Reference Waldspurger11] 1.3 pour la définition de cette propriété. On note
$G_{\sharp }(F)$
qui sont tempérées et de réduction unipotente, cf. [Reference Waldspurger11] 1.3 pour la définition de cette propriété. On note
![]() $\operatorname{Irr}_{\operatorname{tunip}}$
la réunion disjointe de
$\operatorname{Irr}_{\operatorname{tunip}}$
la réunion disjointe de
![]() $\operatorname{Irr}_{\operatorname{tunip},\operatorname{iso}}$
et
$\operatorname{Irr}_{\operatorname{tunip},\operatorname{iso}}$
et
![]() $\operatorname{Irr}_{\operatorname{tunip},\operatorname{an}}$
. Pour une partition symplectique
$\operatorname{Irr}_{\operatorname{tunip},\operatorname{an}}$
. Pour une partition symplectique
![]() $\unicode[STIX]{x1D706}$
de
$\unicode[STIX]{x1D706}$
de
![]() $2n$
, fixons un homomorphisme algébrique
$2n$
, fixons un homomorphisme algébrique
![]() $\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D706}}:\text{SL}(2;\mathbb{C})\rightarrow \operatorname{Sp}(2n;\mathbb{C})$
paramétré par
$\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D706}}:\text{SL}(2;\mathbb{C})\rightarrow \operatorname{Sp}(2n;\mathbb{C})$
paramétré par
![]() $\unicode[STIX]{x1D706}$
, cf. [Reference Waldspurger11] 1.3. On note
$\unicode[STIX]{x1D706}$
, cf. [Reference Waldspurger11] 1.3. On note
![]() $Z(\unicode[STIX]{x1D706})$
le commutant dans
$Z(\unicode[STIX]{x1D706})$
le commutant dans
![]() $\operatorname{Sp}(2n;\mathbb{C})$
de l’image de
$\operatorname{Sp}(2n;\mathbb{C})$
de l’image de
![]() $\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D706}}$
. Soit
$\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D706}}$
. Soit
![]() $s\in Z(\unicode[STIX]{x1D706})$
un élément semi-simple dont toutes les valeurs propres sont de module
$s\in Z(\unicode[STIX]{x1D706})$
un élément semi-simple dont toutes les valeurs propres sont de module
![]() $1$
. On note
$1$
. On note
![]() $Z(s,\unicode[STIX]{x1D706})$
le commutant de
$Z(s,\unicode[STIX]{x1D706})$
le commutant de
![]() $s$
dans
$s$
dans
![]() $Z(\unicode[STIX]{x1D706})$
,
$Z(\unicode[STIX]{x1D706})$
,
![]() $\mathbf{Z}(\unicode[STIX]{x1D706},s)$
son groupe de composantes connexes et
$\mathbf{Z}(\unicode[STIX]{x1D706},s)$
son groupe de composantes connexes et
![]() $\mathbf{Z}(\unicode[STIX]{x1D706},s)^{\vee }$
le groupe des caractères de
$\mathbf{Z}(\unicode[STIX]{x1D706},s)^{\vee }$
le groupe des caractères de
![]() $\mathbf{Z}(\unicode[STIX]{x1D706},s)$
. On a vu en [Reference Waldspurger11] 1.3 que l’on pouvait présenter la paramétrisation de Langlands sous la forme suivante :
$\mathbf{Z}(\unicode[STIX]{x1D706},s)$
. On a vu en [Reference Waldspurger11] 1.3 que l’on pouvait présenter la paramétrisation de Langlands sous la forme suivante :
![]() $\operatorname{Irr}_{\operatorname{tunip}}$
est paramétré par l’ensemble des classes de conjugaison (en un sens facile à préciser) de triplets
$\operatorname{Irr}_{\operatorname{tunip}}$
est paramétré par l’ensemble des classes de conjugaison (en un sens facile à préciser) de triplets
![]() $(\unicode[STIX]{x1D706},s,\unicode[STIX]{x1D716})$
, où
$(\unicode[STIX]{x1D706},s,\unicode[STIX]{x1D716})$
, où
![]() $\unicode[STIX]{x1D706}$
et
$\unicode[STIX]{x1D706}$
et
![]() $s$
sont comme ci-dessus et
$s$
sont comme ci-dessus et
![]() $\unicode[STIX]{x1D716}\in \mathbf{Z}(s,\unicode[STIX]{x1D706})^{\vee }$
. Le paramétrage a été obtenu par différents auteurs : Lusztig, cf. [Reference Lusztig4] ; Moeglin, cf. [Reference Moeglin5] théorème 5.2 ; Arthur, cf. [Reference Arthur1] théorème 2.2.1. Nous utilisons les constructions de Lusztig. Le but de l’article est de prouver que les représentations qu’il a construites vérifient les propriétés relatives à l’endoscopie qui caractérisent la paramétrisation. Pour un triplet
$\unicode[STIX]{x1D716}\in \mathbf{Z}(s,\unicode[STIX]{x1D706})^{\vee }$
. Le paramétrage a été obtenu par différents auteurs : Lusztig, cf. [Reference Lusztig4] ; Moeglin, cf. [Reference Moeglin5] théorème 5.2 ; Arthur, cf. [Reference Arthur1] théorème 2.2.1. Nous utilisons les constructions de Lusztig. Le but de l’article est de prouver que les représentations qu’il a construites vérifient les propriétés relatives à l’endoscopie qui caractérisent la paramétrisation. Pour un triplet
![]() $(\unicode[STIX]{x1D706},s,\unicode[STIX]{x1D716})$
comme ci-dessus, on note
$(\unicode[STIX]{x1D706},s,\unicode[STIX]{x1D716})$
comme ci-dessus, on note
![]() $\unicode[STIX]{x1D70B}(\unicode[STIX]{x1D706},s,\unicode[STIX]{x1D716})$
la représentation qui lui est associée par Lusztig.
$\unicode[STIX]{x1D70B}(\unicode[STIX]{x1D706},s,\unicode[STIX]{x1D716})$
la représentation qui lui est associée par Lusztig.
Soit
![]() $(\unicode[STIX]{x1D706},s)$
comme ci-dessus et soit
$(\unicode[STIX]{x1D706},s)$
comme ci-dessus et soit
![]() $h\in Z(\unicode[STIX]{x1D706},s)$
un élément tel que
$h\in Z(\unicode[STIX]{x1D706},s)$
un élément tel que
![]() $h^{2}=1$
. Pour
$h^{2}=1$
. Pour
![]() $\unicode[STIX]{x1D716}\in \mathbf{Z}(\unicode[STIX]{x1D706},s)^{\vee }$
on note
$\unicode[STIX]{x1D716}\in \mathbf{Z}(\unicode[STIX]{x1D706},s)^{\vee }$
on note
![]() $\unicode[STIX]{x1D716}(h)$
la valeur de
$\unicode[STIX]{x1D716}(h)$
la valeur de
![]() $\unicode[STIX]{x1D716}$
en l’image de
$\unicode[STIX]{x1D716}$
en l’image de
![]() $h$
dans
$h$
dans
![]() $Z(\unicode[STIX]{x1D706},s)$
. On définit la représentation virtuelle
$Z(\unicode[STIX]{x1D706},s)$
. On définit la représentation virtuelle
Pour
![]() $\sharp =\operatorname{iso}$
ou
$\sharp =\operatorname{iso}$
ou
![]() $\operatorname{an}$
, on note
$\operatorname{an}$
, on note
![]() $\unicode[STIX]{x1D6F1}_{\sharp }(\unicode[STIX]{x1D706},s,h)$
la sous-somme où l’on se restreint aux
$\unicode[STIX]{x1D6F1}_{\sharp }(\unicode[STIX]{x1D706},s,h)$
la sous-somme où l’on se restreint aux
![]() $\unicode[STIX]{x1D716}$
tels que
$\unicode[STIX]{x1D716}$
tels que
![]() $\unicode[STIX]{x1D70B}(\unicode[STIX]{x1D706},s,\unicode[STIX]{x1D716})$
soit une représentation de
$\unicode[STIX]{x1D70B}(\unicode[STIX]{x1D706},s,\unicode[STIX]{x1D716})$
soit une représentation de
![]() $G_{\sharp }(F)$
.
$G_{\sharp }(F)$
.
Soit
![]() $n_{1},n_{2}\in \mathbb{N}$
deux entiers tels que
$n_{1},n_{2}\in \mathbb{N}$
deux entiers tels que
![]() $n_{1}+n_{2}=n$
. Un tel couple détermine une donnée endoscopique de
$n_{1}+n_{2}=n$
. Un tel couple détermine une donnée endoscopique de
![]() $G_{\operatorname{iso}}$
ou
$G_{\operatorname{iso}}$
ou
![]() $G_{\operatorname{an}}$
dont le groupe endoscopique est
$G_{\operatorname{an}}$
dont le groupe endoscopique est
![]() $G_{n_{1},\operatorname{iso}}\times G_{n_{2},\operatorname{iso}}$
(ce sont les groupes similaires à
$G_{n_{1},\operatorname{iso}}\times G_{n_{2},\operatorname{iso}}$
(ce sont les groupes similaires à
![]() $G_{\operatorname{iso}}$
quand on remplace
$G_{\operatorname{iso}}$
quand on remplace
![]() $n$
par
$n$
par
![]() $n_{1}$
ou
$n_{1}$
ou
![]() $n_{2}$
). Soit
$n_{2}$
). Soit
![]() $(\unicode[STIX]{x1D706}_{1},s_{1},h_{1})$
et
$(\unicode[STIX]{x1D706}_{1},s_{1},h_{1})$
et
![]() $(\unicode[STIX]{x1D706}_{2},s_{2},h_{2})$
des triplets similaires au triplet
$(\unicode[STIX]{x1D706}_{2},s_{2},h_{2})$
des triplets similaires au triplet
![]() $(\unicode[STIX]{x1D706},s,h)$
ci-dessus, relatifs aux entiers
$(\unicode[STIX]{x1D706},s,h)$
ci-dessus, relatifs aux entiers
![]() $n_{1}$
et
$n_{1}$
et
![]() $n_{2}$
. Supposons que
$n_{2}$
. Supposons que
![]() $h_{1}=1$
et
$h_{1}=1$
et
![]() $h_{2}=1$
. Comme on l’a prouvé dans [Reference Moeglin and Waldspurger6], les caractères de
$h_{2}=1$
. Comme on l’a prouvé dans [Reference Moeglin and Waldspurger6], les caractères de
![]() $\unicode[STIX]{x1D6F1}_{\operatorname{iso}}(\unicode[STIX]{x1D706}_{1},s_{1},1)$
et
$\unicode[STIX]{x1D6F1}_{\operatorname{iso}}(\unicode[STIX]{x1D706}_{1},s_{1},1)$
et
![]() $\unicode[STIX]{x1D6F1}_{\operatorname{iso}}(\unicode[STIX]{x1D706}_{2},s_{2},1)$
sont des distributions stables et, en identifiant les représentations à leurs caractères, on définit le transfert à
$\unicode[STIX]{x1D6F1}_{\operatorname{iso}}(\unicode[STIX]{x1D706}_{2},s_{2},1)$
sont des distributions stables et, en identifiant les représentations à leurs caractères, on définit le transfert à
![]() $G_{\operatorname{iso}}(F)$
ou
$G_{\operatorname{iso}}(F)$
ou
![]() $G_{\operatorname{an}}(F)$
de
$G_{\operatorname{an}}(F)$
de
![]() $\unicode[STIX]{x1D6F1}_{\operatorname{iso}}(\unicode[STIX]{x1D706}_{1},s_{1},1)\,\otimes \,\unicode[STIX]{x1D6F1}_{\operatorname{iso}}(\unicode[STIX]{x1D706}_{2},s_{2},1)$
. À l’aide des triplets
$\unicode[STIX]{x1D6F1}_{\operatorname{iso}}(\unicode[STIX]{x1D706}_{1},s_{1},1)\,\otimes \,\unicode[STIX]{x1D6F1}_{\operatorname{iso}}(\unicode[STIX]{x1D706}_{2},s_{2},1)$
. À l’aide des triplets
![]() $(\unicode[STIX]{x1D706}_{1},s_{1},h_{1})$
et
$(\unicode[STIX]{x1D706}_{1},s_{1},h_{1})$
et
![]() $(\unicode[STIX]{x1D706}_{2},s_{2},h_{2})$
et du couple
$(\unicode[STIX]{x1D706}_{2},s_{2},h_{2})$
et du couple
![]() $(n_{1},n_{2})$
, on construit naturellement un triplet
$(n_{1},n_{2})$
, on construit naturellement un triplet
![]() $(\unicode[STIX]{x1D706},s,h)$
pour l’entier
$(\unicode[STIX]{x1D706},s,h)$
pour l’entier
![]() $n$
, cf. [Reference Waldspurger11] 2.1. En particulier,
$n$
, cf. [Reference Waldspurger11] 2.1. En particulier,
![]() $h$
a pour valeurs propres
$h$
a pour valeurs propres
![]() $1$
avec la multiplicité
$1$
avec la multiplicité
![]() $2n_{1}$
et
$2n_{1}$
et
![]() $-1$
avec la multiplicité
$-1$
avec la multiplicité
![]() $2n_{2}$
.
$2n_{2}$
.
Théorème. Le transfert de
![]() $\unicode[STIX]{x1D6F1}_{\operatorname{iso}}(\unicode[STIX]{x1D706}_{1},s_{1},1)\,\otimes \,\unicode[STIX]{x1D6F1}_{\operatorname{iso}}(\unicode[STIX]{x1D706}_{2},s_{2},1)$
à
$\unicode[STIX]{x1D6F1}_{\operatorname{iso}}(\unicode[STIX]{x1D706}_{1},s_{1},1)\,\otimes \,\unicode[STIX]{x1D6F1}_{\operatorname{iso}}(\unicode[STIX]{x1D706}_{2},s_{2},1)$
à
![]() $G_{\operatorname{iso}}(F)$
est
$G_{\operatorname{iso}}(F)$
est
![]() $\unicode[STIX]{x1D6F1}_{\operatorname{iso}}(\unicode[STIX]{x1D706},s,h)$
. Le transfert de
$\unicode[STIX]{x1D6F1}_{\operatorname{iso}}(\unicode[STIX]{x1D706},s,h)$
. Le transfert de
![]() $\unicode[STIX]{x1D6F1}_{\operatorname{iso}}(\unicode[STIX]{x1D706}_{1},s_{1},1)\,\otimes \,\unicode[STIX]{x1D6F1}_{\operatorname{iso}}(\unicode[STIX]{x1D706}_{2},s_{2},1)$
à
$\unicode[STIX]{x1D6F1}_{\operatorname{iso}}(\unicode[STIX]{x1D706}_{1},s_{1},1)\,\otimes \,\unicode[STIX]{x1D6F1}_{\operatorname{iso}}(\unicode[STIX]{x1D706}_{2},s_{2},1)$
à
![]() $G_{\operatorname{an}}(F)$
est
$G_{\operatorname{an}}(F)$
est
![]() $-\unicode[STIX]{x1D6F1}_{\operatorname{an}}(\unicode[STIX]{x1D706},s,h)$
.
$-\unicode[STIX]{x1D6F1}_{\operatorname{an}}(\unicode[STIX]{x1D706},s,h)$
.
On a énoncé ce résultat en [Reference Waldspurger11] 2.1 et on va maintenant le prouver.
La preuve reprend étroitement celle de [Reference Moeglin and Waldspurger6]. On se ramène par induction au cas où les représentations considérées sont elliptiques au sens d’Arthur. D’après le résultat de [Reference Arthur2], il suffit alors de comparer les valeurs de leurs caractères sur des éléments elliptiques fortement réguliers de nos différents groupes. Ce sont les intégrales orbitales de leurs pseudocoefficients. On a déjà calculé ces derniers dans [Reference Moeglin and Waldspurger6]. À l’aide des travaux de Lusztig et de l’involution que l’on a définie dans [Reference Moeglin and Waldspurger6] (on a repris sa définition dans [Reference Waldspurger11]), on obtient une expression des caractères en termes d’intégrales orbitales de fonctions de Green. Ces fonctions ont été définies sous leur forme la plus générale par Lusztig. Elle vivent sur des groupes finis mais on en déduit par un procédé usuel d’inflation des fonctions sur nos groupes
![]() $G_{\operatorname{iso}}(F)$
et
$G_{\operatorname{iso}}(F)$
et
![]() $G_{\operatorname{an}}(F)$
(ou leurs groupes endoscopiques). Il reste à démontrer un résultat de transfert entre fonctions de Green. Ces fonctions étant à support topologiquement unipotent, on descend facilement aux algèbres de Lie. On se rappelle que, d’après Harish-Chandra, la transformée de Fourier d’une intégrale orbitale est une distribution localement intégrable et peut donc être considérée comme une fonction. Selon une idée qui remonte à Springer, on a exprimé dans [Reference Waldspurger9] puis dans [Reference Moeglin and Waldspurger6] les intégrales orbitales des fonctions de Green comme des combinaisons linéaires explicites de transformées de Fourier de certaines intégrales orbitales relatives à des éléments semi-simples réguliers. Puisque le transfert endoscopique commute à des constantes près aux transformations de Fourier, on est ramené à transférer de telles intégrales orbitales, ce qui est à peu près tautologique.
$G_{\operatorname{an}}(F)$
(ou leurs groupes endoscopiques). Il reste à démontrer un résultat de transfert entre fonctions de Green. Ces fonctions étant à support topologiquement unipotent, on descend facilement aux algèbres de Lie. On se rappelle que, d’après Harish-Chandra, la transformée de Fourier d’une intégrale orbitale est une distribution localement intégrable et peut donc être considérée comme une fonction. Selon une idée qui remonte à Springer, on a exprimé dans [Reference Waldspurger9] puis dans [Reference Moeglin and Waldspurger6] les intégrales orbitales des fonctions de Green comme des combinaisons linéaires explicites de transformées de Fourier de certaines intégrales orbitales relatives à des éléments semi-simples réguliers. Puisque le transfert endoscopique commute à des constantes près aux transformations de Fourier, on est ramené à transférer de telles intégrales orbitales, ce qui est à peu près tautologique.
Comme on l’a dit, ce schéma de démonstration se trouve déjà dans [Reference Moeglin and Waldspurger6] où on s’était limité à prouver des résultats de stabilité. Pour obtenir les égalités endoscopiques, il suffit de poursuivre les calculs un peu plus loin. Ce n’est sans doute pas très passionnant, mais les calculs sont suffisamment compliqués pour mériter, à ce qu’il nous semble, d’être présentés en détail. Ces calculs sont en particulier compliqués par la présence de constantes terrifiques. À l’évidence, les normalisations de nos divers objets que nous avons choisies ne sont pas les bonnes. Il nous a toutefois semblé préférable de les conserver, car cela permet de rendre compréhensibles les références à nos articles antérieurs.
1 Les résultats
1.1 Calcul des caractères sur les éléments compacts
Pour tout groupe réductif défini sur
![]() $F$
ou
$F$
ou
![]() $\mathbb{F}_{q}$
(qui est le corps résiduel de
$\mathbb{F}_{q}$
(qui est le corps résiduel de
![]() $F$
), noté
$F$
), noté
![]() $H$
, on note par la lettre gothique
$H$
, on note par la lettre gothique
![]() $\mathfrak{h}$
son algèbre de Lie. Fixons un caractère continu
$\mathfrak{h}$
son algèbre de Lie. Fixons un caractère continu
![]() $\unicode[STIX]{x1D713}_{F}:F\rightarrow \mathbb{C}^{\times }$
de conducteur l’idéal maximal
$\unicode[STIX]{x1D713}_{F}:F\rightarrow \mathbb{C}^{\times }$
de conducteur l’idéal maximal
![]() $\unicode[STIX]{x1D71B}\mathfrak{o}$
. Pour
$\unicode[STIX]{x1D71B}\mathfrak{o}$
. Pour
![]() $\sharp =\operatorname{iso}$
ou
$\sharp =\operatorname{iso}$
ou
![]() $\operatorname{an}$
, l’algèbre de Lie
$\operatorname{an}$
, l’algèbre de Lie
![]() $\mathfrak{g}_{\sharp }(F)$
s’identifie naturellement à un sous-espace de l’algèbre des endomorphismes de
$\mathfrak{g}_{\sharp }(F)$
s’identifie naturellement à un sous-espace de l’algèbre des endomorphismes de
![]() $V_{\sharp }$
. Ainsi,
$V_{\sharp }$
. Ainsi,
![]() $\operatorname{trace}(XY)$
est bien définie pour
$\operatorname{trace}(XY)$
est bien définie pour
![]() $X,Y\in \mathfrak{g}_{\sharp }(F)$
. On introduit une transformation de Fourier
$X,Y\in \mathfrak{g}_{\sharp }(F)$
. On introduit une transformation de Fourier
![]() $f\mapsto \hat{f}$
dans
$f\mapsto \hat{f}$
dans
![]() $C_{c}^{\infty }(\mathfrak{g}_{\sharp }(F))$
par la formule usuelle
$C_{c}^{\infty }(\mathfrak{g}_{\sharp }(F))$
par la formule usuelle
Le mesure
![]() $dY$
est la mesure de Haar sur
$dY$
est la mesure de Haar sur
![]() $\mathfrak{g}_{\sharp }(F)$
qui est autoduale, c’est-à-dire que
$\mathfrak{g}_{\sharp }(F)$
qui est autoduale, c’est-à-dire que
![]() $\hat{\hat{f}}(X)=f(-X)$
pour tous
$\hat{\hat{f}}(X)=f(-X)$
pour tous
![]() $f$
,
$f$
,
![]() $X$
. L’exponentielle
$X$
. L’exponentielle
![]() $\text{exp}$
est bien définie dans un voisinage de
$\text{exp}$
est bien définie dans un voisinage de
![]() $0$
dans
$0$
dans
![]() $\mathfrak{g}_{\sharp }(F)$
, à valeurs dans un voisinage de
$\mathfrak{g}_{\sharp }(F)$
, à valeurs dans un voisinage de
![]() $1$
dans
$1$
dans
![]() $G_{\sharp }(F)$
. On munit
$G_{\sharp }(F)$
. On munit
![]() $G_{\sharp }(F)$
de la mesure de Haar telle que le jacobien de l’exponentielle vaille
$G_{\sharp }(F)$
de la mesure de Haar telle que le jacobien de l’exponentielle vaille
![]() $1$
au point
$1$
au point
![]() $0$
.
$0$
.
Soit
![]() $x\in G_{\sharp }(F)$
un élément fortement régulier et compact (cf. [Reference Waldspurger11] 1.2). Soit
$x\in G_{\sharp }(F)$
un élément fortement régulier et compact (cf. [Reference Waldspurger11] 1.2). Soit
![]() $f\in C_{c}^{\infty }(G_{\sharp }(F))$
. On définit l’intégrale orbitale
$f\in C_{c}^{\infty }(G_{\sharp }(F))$
. On définit l’intégrale orbitale
où
![]() $D^{G_{\sharp }}$
est le module de Weyl usuel. Si maintenant
$D^{G_{\sharp }}$
est le module de Weyl usuel. Si maintenant
![]() $f=(f_{\operatorname{iso}},f_{\operatorname{an}})\in C_{c}^{\infty }(G_{\operatorname{iso}}(F))\oplus C_{c}^{\infty }(G_{\operatorname{an}}(F))$
et si
$f=(f_{\operatorname{iso}},f_{\operatorname{an}})\in C_{c}^{\infty }(G_{\operatorname{iso}}(F))\oplus C_{c}^{\infty }(G_{\operatorname{an}}(F))$
et si
![]() $x\in G_{\sharp }(F)$
est comme ci-dessus, on pose
$x\in G_{\sharp }(F)$
est comme ci-dessus, on pose
![]() $J(x,f)=J(x,f_{\sharp })$
.
$J(x,f)=J(x,f_{\sharp })$
.
On a défini un espace
![]() ${\mathcal{R}}^{\operatorname{par}}$
en [Reference Waldspurger11] 1.5. On définit une application linéaire
${\mathcal{R}}^{\operatorname{par}}$
en [Reference Waldspurger11] 1.5. On définit une application linéaire
![]() $\unicode[STIX]{x1D6F9}:{\mathcal{R}}^{\operatorname{par}}\rightarrow C_{c}^{\infty }(G_{\operatorname{iso}}(F))\oplus C_{c}^{\infty }(G_{\operatorname{an}}(F))$
de la façon suivante. Par linéarité, il suffit de fixer
$\unicode[STIX]{x1D6F9}:{\mathcal{R}}^{\operatorname{par}}\rightarrow C_{c}^{\infty }(G_{\operatorname{iso}}(F))\oplus C_{c}^{\infty }(G_{\operatorname{an}}(F))$
de la façon suivante. Par linéarité, il suffit de fixer
![]() $\sharp =\operatorname{iso}$
ou
$\sharp =\operatorname{iso}$
ou
![]() $\operatorname{an}$
et
$\operatorname{an}$
et
![]() $(n^{\prime },n^{\prime \prime })\in D_{\sharp }(n)$
, et de la définir sur la composante
$(n^{\prime },n^{\prime \prime })\in D_{\sharp }(n)$
, et de la définir sur la composante
![]() $C_{n^{\prime }}^{\prime }\,\otimes \,C_{n^{\prime \prime },\sharp }^{\prime \prime }$
de
$C_{n^{\prime }}^{\prime }\,\otimes \,C_{n^{\prime \prime },\sharp }^{\prime \prime }$
de
![]() ${\mathcal{R}}^{\operatorname{par}}$
. Soit donc
${\mathcal{R}}^{\operatorname{par}}$
. Soit donc
![]() $\unicode[STIX]{x1D711}\in C_{n^{\prime }}^{\prime }\,\otimes \,C_{n^{\prime \prime },\sharp }^{\prime \prime }$
. C’est une fonction sur
$\unicode[STIX]{x1D711}\in C_{n^{\prime }}^{\prime }\,\otimes \,C_{n^{\prime \prime },\sharp }^{\prime \prime }$
. C’est une fonction sur
![]() $\mathbf{SO}(2n^{\prime }+1;\mathbb{F}_{q})\times \mathbf{O}(2n^{\prime \prime })_{\sharp }(\mathbb{F}_{q})$
. On introduit le sous-groupe
$\mathbf{SO}(2n^{\prime }+1;\mathbb{F}_{q})\times \mathbf{O}(2n^{\prime \prime })_{\sharp }(\mathbb{F}_{q})$
. On introduit le sous-groupe
![]() $K_{n^{\prime },n^{\prime \prime }}^{\pm }$
de
$K_{n^{\prime },n^{\prime \prime }}^{\pm }$
de
![]() $G_{\sharp }(F)$
, cf. [Reference Waldspurger11] 1.2. Le groupe précédent s’identifie à
$G_{\sharp }(F)$
, cf. [Reference Waldspurger11] 1.2. Le groupe précédent s’identifie à
![]() $K_{n^{\prime },n^{\prime \prime }}^{\pm }/K_{n^{\prime },n^{\prime \prime }}^{u}$
. Alors
$K_{n^{\prime },n^{\prime \prime }}^{\pm }/K_{n^{\prime },n^{\prime \prime }}^{u}$
. Alors
![]() $\unicode[STIX]{x1D711}$
apparaît comme une fonction sur
$\unicode[STIX]{x1D711}$
apparaît comme une fonction sur
![]() $K_{n^{\prime },n^{\prime \prime }}^{\pm }$
, invariante par
$K_{n^{\prime },n^{\prime \prime }}^{\pm }$
, invariante par
![]() $K_{n^{\prime },n^{\prime \prime }}^{u}$
. On la prolonge par
$K_{n^{\prime },n^{\prime \prime }}^{u}$
. On la prolonge par
![]() $0$
hors de
$0$
hors de
![]() $K_{n^{\prime },n^{\prime \prime }}^{\pm }$
et on la multiplie par
$K_{n^{\prime },n^{\prime \prime }}^{\pm }$
et on la multiplie par
![]() $\text{mes}(K_{n^{\prime },n^{\prime \prime }}^{\pm })^{-1}$
. On obtient un élément de
$\text{mes}(K_{n^{\prime },n^{\prime \prime }}^{\pm })^{-1}$
. On obtient un élément de
![]() $C_{c}^{\infty }(G_{\sharp }(F))$
qui est l’une des composantes de
$C_{c}^{\infty }(G_{\sharp }(F))$
qui est l’une des composantes de
![]() $\unicode[STIX]{x1D6F9}(\unicode[STIX]{x1D711})$
. L’autre composante est nulle.
$\unicode[STIX]{x1D6F9}(\unicode[STIX]{x1D711})$
. L’autre composante est nulle.
Soit
![]() $\sharp =\operatorname{iso}$
ou
$\sharp =\operatorname{iso}$
ou
![]() $\operatorname{an}$
et soit
$\operatorname{an}$
et soit
![]() $\unicode[STIX]{x1D70B}\in \operatorname{Irr}_{\operatorname{unip},\sharp }$
, cf. [Reference Waldspurger11] 1.3. Pour
$\unicode[STIX]{x1D70B}\in \operatorname{Irr}_{\operatorname{unip},\sharp }$
, cf. [Reference Waldspurger11] 1.3. Pour
![]() $f\in C_{c}^{\infty }(G_{\sharp }(F))$
, on définit l’opérateur
$f\in C_{c}^{\infty }(G_{\sharp }(F))$
, on définit l’opérateur
![]() $\unicode[STIX]{x1D70B}(f)$
. Il est de rang fini et possède une trace. D’après Harish-Chandra, il existe une fonction localement intégrable
$\unicode[STIX]{x1D70B}(f)$
. Il est de rang fini et possède une trace. D’après Harish-Chandra, il existe une fonction localement intégrable
![]() $\unicode[STIX]{x1D6E9}_{\unicode[STIX]{x1D70B}}$
sur
$\unicode[STIX]{x1D6E9}_{\unicode[STIX]{x1D70B}}$
sur
![]() $G_{\sharp }(F)$
, localement constante sur les éléments fortement réguliers, de sorte que
$G_{\sharp }(F)$
, localement constante sur les éléments fortement réguliers, de sorte que
pour tout
![]() $f$
. Posons
$f$
. Posons
![]() $f_{\unicode[STIX]{x1D70B}}=\unicode[STIX]{x1D6F9}\circ \operatorname{proj}_{\operatorname{cusp}}\circ \operatorname{Res}(\unicode[STIX]{x1D70B})$
, avec les notations de [Reference Waldspurger11] 1.5.
$f_{\unicode[STIX]{x1D70B}}=\unicode[STIX]{x1D6F9}\circ \operatorname{proj}_{\operatorname{cusp}}\circ \operatorname{Res}(\unicode[STIX]{x1D70B})$
, avec les notations de [Reference Waldspurger11] 1.5.
Proposition. Soit
![]() $x\in G_{\sharp }(F)$
un élément fortement régulier et compact. On a l’égalité
$x\in G_{\sharp }(F)$
un élément fortement régulier et compact. On a l’égalité
Cela résulte de [Reference Moeglin and Waldspurger6] théorème 1.9 et lemme 4.2.
1.2 Un résultat de transfert de fonctions
Pour
![]() $\sharp =\operatorname{iso}$
ou
$\sharp =\operatorname{iso}$
ou
![]() $\operatorname{an}$
et pour
$\operatorname{an}$
et pour
![]() $f\in C_{c}^{\infty }(G_{\sharp }(F))$
, on dit que
$f\in C_{c}^{\infty }(G_{\sharp }(F))$
, on dit que
![]() $f$
est cuspidale si et seulement si ses intégrales orbitales sont nulles en tout point fortement régulier et non elliptique de
$f$
est cuspidale si et seulement si ses intégrales orbitales sont nulles en tout point fortement régulier et non elliptique de
![]() $G_{\sharp }(F)$
. On note
$G_{\sharp }(F)$
. On note
![]() $C_{\operatorname{cusp}}^{\infty }(G_{\sharp }(F))$
l’espace des fonctions cuspidales. L’application
$C_{\operatorname{cusp}}^{\infty }(G_{\sharp }(F))$
l’espace des fonctions cuspidales. L’application
![]() $\unicode[STIX]{x1D6F9}:{\mathcal{R}}^{\operatorname{par}}\rightarrow C_{c}^{\infty }(G_{\operatorname{iso}}(F))\oplus C_{c}^{\infty }(G_{\operatorname{an}}(F))$
introduite en 1.1 envoie l’espace
$\unicode[STIX]{x1D6F9}:{\mathcal{R}}^{\operatorname{par}}\rightarrow C_{c}^{\infty }(G_{\operatorname{iso}}(F))\oplus C_{c}^{\infty }(G_{\operatorname{an}}(F))$
introduite en 1.1 envoie l’espace
![]() ${\mathcal{R}}_{\operatorname{cusp}}^{\operatorname{par}}$
de [Reference Waldspurger11] 1.5 dans
${\mathcal{R}}_{\operatorname{cusp}}^{\operatorname{par}}$
de [Reference Waldspurger11] 1.5 dans
![]() $C_{\operatorname{cusp}}^{\infty }(G_{\operatorname{iso}}(F))\oplus C_{\operatorname{cusp}}^{\infty }(G_{\operatorname{an}}(F))$
. Pour un élément
$C_{\operatorname{cusp}}^{\infty }(G_{\operatorname{iso}}(F))\oplus C_{\operatorname{cusp}}^{\infty }(G_{\operatorname{an}}(F))$
. Pour un élément
![]() $f$
de ce dernier espace, on note
$f$
de ce dernier espace, on note
![]() $f_{\operatorname{iso}}$
et
$f_{\operatorname{iso}}$
et
![]() $f_{\operatorname{an}}$
ses deux composantes.
$f_{\operatorname{an}}$
ses deux composantes.
Il nous faut adapter les définitions usuelles de l’endoscopie à notre cas où nous travaillons simultanément avec nos deux groupes
![]() $G_{\operatorname{iso}}$
et
$G_{\operatorname{iso}}$
et
![]() $G_{\operatorname{an}}$
. Pour
$G_{\operatorname{an}}$
. Pour
![]() $x,y\in G_{\operatorname{iso}}(F)\cup G_{\operatorname{an}}(F)$
, on dit que
$x,y\in G_{\operatorname{iso}}(F)\cup G_{\operatorname{an}}(F)$
, on dit que
![]() $x$
et
$x$
et
![]() $y$
sont conjugués si et seulement si il existe
$y$
sont conjugués si et seulement si il existe
![]() $\sharp =\operatorname{iso}$
ou
$\sharp =\operatorname{iso}$
ou
![]() $\operatorname{an}$
tels que
$\operatorname{an}$
tels que
![]() $x,y\in G_{\sharp }(F)$
et
$x,y\in G_{\sharp }(F)$
et
![]() $x$
et
$x$
et
![]() $y$
sont conjugués par un élément de
$y$
sont conjugués par un élément de
![]() $G_{\sharp }(F)$
. Il y a une correspondance bijective entre les classes de conjugaison stable dans
$G_{\sharp }(F)$
. Il y a une correspondance bijective entre les classes de conjugaison stable dans
![]() $G_{\operatorname{iso}}(F)$
formées d’éléments elliptiques et fortement réguliers et les classes de conjugaison stable dans
$G_{\operatorname{iso}}(F)$
formées d’éléments elliptiques et fortement réguliers et les classes de conjugaison stable dans
![]() $G_{\operatorname{an}}(F)$
formées d’éléments elliptiques et fortement réguliers. Appelons classe totale de conjugaison stable (formée d’éléments elliptiques et fortement réguliers) la réunion d’une telle classe dans
$G_{\operatorname{an}}(F)$
formées d’éléments elliptiques et fortement réguliers. Appelons classe totale de conjugaison stable (formée d’éléments elliptiques et fortement réguliers) la réunion d’une telle classe dans
![]() $G_{\operatorname{iso}}(F)$
et de celle qui lui correspond dans
$G_{\operatorname{iso}}(F)$
et de celle qui lui correspond dans
![]() $G_{\operatorname{an}}(F)$
. On sait d’ailleurs que chacune de ces classes contient le même nombre de classes de conjugaison (ordinaires).
$G_{\operatorname{an}}(F)$
. On sait d’ailleurs que chacune de ces classes contient le même nombre de classes de conjugaison (ordinaires).
Soit
![]() $f\in C_{\operatorname{cusp}}^{\infty }(G_{\operatorname{iso}}(F))\oplus C_{\operatorname{cusp}}^{\infty }(G_{\operatorname{an}}(F))$
et soit
$f\in C_{\operatorname{cusp}}^{\infty }(G_{\operatorname{iso}}(F))\oplus C_{\operatorname{cusp}}^{\infty }(G_{\operatorname{an}}(F))$
et soit
![]() $x\in G_{\operatorname{iso}}(F)$
un élément fortement régulier et elliptique. On définit l’intégrale orbitale stable
$x\in G_{\operatorname{iso}}(F)$
un élément fortement régulier et elliptique. On définit l’intégrale orbitale stable
![]() $S(x,f)$
par
$S(x,f)$
par
où
![]() $y$
parcourt les éléments de la classe totale de conjugaison stable de
$y$
parcourt les éléments de la classe totale de conjugaison stable de
![]() $x$
, à conjugaison près. On note
$x$
, à conjugaison près. On note
![]() $z(x)$
le nombre de termes
$z(x)$
le nombre de termes
![]() $y$
intervenant dans cette somme. Pour
$y$
intervenant dans cette somme. Pour
![]() $\sharp =\operatorname{iso}$
ou
$\sharp =\operatorname{iso}$
ou
![]() $\operatorname{an}$
et
$\operatorname{an}$
et
![]() $f\in C_{c}^{\infty }(G_{\sharp }(F))$
, on définit
$f\in C_{c}^{\infty }(G_{\sharp }(F))$
, on définit
![]() $S(x,f)$
en considérant que
$S(x,f)$
en considérant que
![]() $f$
est un élément de
$f$
est un élément de
![]() $C_{\operatorname{cusp}}^{\infty }(G_{\operatorname{iso}}(F))\oplus C_{\operatorname{cusp}}^{\infty }(G_{\operatorname{an}}(F))$
dont la composante sur
$C_{\operatorname{cusp}}^{\infty }(G_{\operatorname{iso}}(F))\oplus C_{\operatorname{cusp}}^{\infty }(G_{\operatorname{an}}(F))$
dont la composante sur
![]() $G_{\sharp }(F)$
est la fonction donnée et dont l’autre composante est nulle.
$G_{\sharp }(F)$
est la fonction donnée et dont l’autre composante est nulle.
Soit
![]() $(n_{1},n_{2})\in D(n)$
. Ce couple détermine (à conjugaison près) un élément
$(n_{1},n_{2})\in D(n)$
. Ce couple détermine (à conjugaison près) un élément
![]() $h\in \operatorname{Sp}(2n;\mathbb{C})$
tel que
$h\in \operatorname{Sp}(2n;\mathbb{C})$
tel que
![]() $h^{2}=1$
et une donnée endoscopique de
$h^{2}=1$
et une donnée endoscopique de
![]() $G_{\operatorname{iso}}$
ou
$G_{\operatorname{iso}}$
ou
![]() $G_{\operatorname{an}}$
dont le groupe endoscopique est
$G_{\operatorname{an}}$
dont le groupe endoscopique est
![]() $G_{n_{1},\operatorname{iso}}\times G_{n_{2},\operatorname{iso}}$
, cf. [Reference Waldspurger11] 2.1. On note
$G_{n_{1},\operatorname{iso}}\times G_{n_{2},\operatorname{iso}}$
, cf. [Reference Waldspurger11] 2.1. On note
![]() $\unicode[STIX]{x1D6E5}_{h}$
le facteur de transfert relatif à cette donnée (il est uniquement déterminé).
$\unicode[STIX]{x1D6E5}_{h}$
le facteur de transfert relatif à cette donnée (il est uniquement déterminé).
Remarque.
Comme on l’a expliqué en [Reference Waldspurger11] 2.1, quand on travaille comme nous le faisons avec nos deux groupes
![]() $G_{\operatorname{iso}}$
et
$G_{\operatorname{iso}}$
et
![]() $G_{\operatorname{an}}$
, les données endoscopiques associées à
$G_{\operatorname{an}}$
, les données endoscopiques associées à
![]() $(n_{1},n_{2})$
et
$(n_{1},n_{2})$
et
![]() $(n_{2},n_{1})$
ne sont pas équivalentes si
$(n_{2},n_{1})$
ne sont pas équivalentes si
![]() $n_{1}\not =n_{2}$
(les facteurs de transfert
$n_{1}\not =n_{2}$
(les facteurs de transfert
![]() $\unicode[STIX]{x1D6E5}_{h}$
et
$\unicode[STIX]{x1D6E5}_{h}$
et
![]() $\unicode[STIX]{x1D6E5}_{-h}$
sont égaux sur
$\unicode[STIX]{x1D6E5}_{-h}$
sont égaux sur
![]() $G_{\operatorname{iso}}(F)$
mais opposés sur
$G_{\operatorname{iso}}(F)$
mais opposés sur
![]() $G_{\operatorname{an}}(F)$
). Dans le cas
$G_{\operatorname{an}}(F)$
). Dans le cas
![]() $n_{1}=n_{2}$
, la permutation des deux facteurs du groupe endoscopique n’est pas un automorphisme de la donnée.
$n_{1}=n_{2}$
, la permutation des deux facteurs du groupe endoscopique n’est pas un automorphisme de la donnée.
Soit
![]() $f\in C_{\operatorname{cusp}}^{\infty }(G_{\operatorname{iso}}(F))\oplus C_{\operatorname{cusp}}^{\infty }(G_{\operatorname{an}}(F))$
et
$f\in C_{\operatorname{cusp}}^{\infty }(G_{\operatorname{iso}}(F))\oplus C_{\operatorname{cusp}}^{\infty }(G_{\operatorname{an}}(F))$
et
![]() $(x_{1},x_{2})\in G_{n_{1},\operatorname{iso}}(F)\times G_{n_{2},\operatorname{iso}}(F)$
un couple
$(x_{1},x_{2})\in G_{n_{1},\operatorname{iso}}(F)\times G_{n_{2},\operatorname{iso}}(F)$
un couple
![]() $n$
-régulier formé d’éléments elliptiques. On entend par
$n$
-régulier formé d’éléments elliptiques. On entend par
![]() $n$
-régulier le fait que la classe de conjugaison stable de
$n$
-régulier le fait que la classe de conjugaison stable de
![]() $(x_{1},x_{2})$
correspond par endoscopie à une classe de conjugaison stable fortement régulière dans
$(x_{1},x_{2})$
correspond par endoscopie à une classe de conjugaison stable fortement régulière dans
![]() $G_{\operatorname{iso}}(F)$
. On pose
$G_{\operatorname{iso}}(F)$
. On pose
où
![]() $x$
parcourt les éléments de
$x$
parcourt les éléments de
![]() $G_{\operatorname{iso}}(F)\cup G_{\operatorname{an}}(F)$
fortement réguliers et elliptiques, à conjugaison près. Bien sûr, on peut se limiter aux éléments dans la classe totale de conjugaison stable qui correspond à
$G_{\operatorname{iso}}(F)\cup G_{\operatorname{an}}(F)$
fortement réguliers et elliptiques, à conjugaison près. Bien sûr, on peut se limiter aux éléments dans la classe totale de conjugaison stable qui correspond à
![]() $(x_{1},x_{2})$
(en dehors, les facteurs de transfert sont nuls). La somme est donc finie. Dans le cas où
$(x_{1},x_{2})$
(en dehors, les facteurs de transfert sont nuls). La somme est donc finie. Dans le cas où
![]() $n_{1}=n$
et
$n_{1}=n$
et
![]() $n_{2}=0$
, où
$n_{2}=0$
, où
![]() $(x_{1},x_{2})$
se réduit à un seul élément
$(x_{1},x_{2})$
se réduit à un seul élément
![]() $x=x_{1}$
, on retrouve la définition précédente :
$x=x_{1}$
, on retrouve la définition précédente :
![]() $J^{\operatorname{endo}}(x_{1},x_{2},f)=S(x,f)$
. Comme ci-dessus, pour
$J^{\operatorname{endo}}(x_{1},x_{2},f)=S(x,f)$
. Comme ci-dessus, pour
![]() $\sharp =\operatorname{iso}$
ou
$\sharp =\operatorname{iso}$
ou
![]() $\operatorname{an}$
et
$\operatorname{an}$
et
![]() $f\in C_{c}^{\infty }(G_{\sharp }(F))$
, on définit
$f\in C_{c}^{\infty }(G_{\sharp }(F))$
, on définit
![]() $J^{\operatorname{endo}}(x_{1},x_{2},f)$
en considérant
$J^{\operatorname{endo}}(x_{1},x_{2},f)$
en considérant
![]() $f$
comme un élément de
$f$
comme un élément de
![]() $C_{\operatorname{cusp}}^{\infty }(G_{\operatorname{iso}}(F))\oplus C_{\operatorname{cusp}}^{\infty }(G_{\operatorname{an}}(F))$
dont une composante est nulle.
$C_{\operatorname{cusp}}^{\infty }(G_{\operatorname{iso}}(F))\oplus C_{\operatorname{cusp}}^{\infty }(G_{\operatorname{an}}(F))$
dont une composante est nulle.
Soit
![]() $(n_{1},n_{2})\in D(n)$
,
$(n_{1},n_{2})\in D(n)$
,
![]() $f\in C_{\operatorname{cusp}}^{\infty }(G_{\operatorname{iso}}(F))\oplus C_{\operatorname{cusp}}^{\infty }(G_{\operatorname{an}}(F))$
,
$f\in C_{\operatorname{cusp}}^{\infty }(G_{\operatorname{iso}}(F))\oplus C_{\operatorname{cusp}}^{\infty }(G_{\operatorname{an}}(F))$
,
![]() $f_{1}\in C_{\operatorname{cusp}}^{\infty }$
$f_{1}\in C_{\operatorname{cusp}}^{\infty }$
![]() $(G_{n_{1},\operatorname{iso}}(F))\oplus \,C_{\operatorname{cusp}}^{\infty }(G_{n_{1},\operatorname{an}}(F))$
et
$(G_{n_{1},\operatorname{iso}}(F))\oplus \,C_{\operatorname{cusp}}^{\infty }(G_{n_{1},\operatorname{an}}(F))$
et
![]() $f_{2}\in C_{\operatorname{cusp}}^{\infty }(G_{n_{2},\operatorname{iso}}(F))\oplus \,C_{\operatorname{cusp}}^{\infty }(G_{n_{2},\operatorname{an}}(F))$
. On dit que
$f_{2}\in C_{\operatorname{cusp}}^{\infty }(G_{n_{2},\operatorname{iso}}(F))\oplus \,C_{\operatorname{cusp}}^{\infty }(G_{n_{2},\operatorname{an}}(F))$
. On dit que
![]() $f_{1}\,\otimes \,f_{2}$
est un transfert de
$f_{1}\,\otimes \,f_{2}$
est un transfert de
![]() $f$
relatif à
$f$
relatif à
![]() $(n_{1},n_{2})$
(ou à
$(n_{1},n_{2})$
(ou à
![]() $h$
) si et seulement si on a l’égalité
$h$
) si et seulement si on a l’égalité
pour tout couple
![]() $n$
-régulier
$n$
-régulier
![]() $(x_{1},x_{2})\in G_{n_{1},\operatorname{iso}}(F)\times G_{n_{2},\operatorname{iso}}(F)$
formé de deux éléments elliptiques.
$(x_{1},x_{2})\in G_{n_{1},\operatorname{iso}}(F)\times G_{n_{2},\operatorname{iso}}(F)$
formé de deux éléments elliptiques.
Soit
![]() $(r^{\prime },r^{\prime \prime },N^{\prime },N^{\prime \prime })\in \unicode[STIX]{x1D6E4}$
, cf. [Reference Waldspurger11] 1.8, et soit
$(r^{\prime },r^{\prime \prime },N^{\prime },N^{\prime \prime })\in \unicode[STIX]{x1D6E4}$
, cf. [Reference Waldspurger11] 1.8, et soit
![]() $\unicode[STIX]{x1D711}^{\prime }\in \mathbb{C}[{\hat{W}}_{N^{\prime }}]_{\operatorname{cusp}}$
et
$\unicode[STIX]{x1D711}^{\prime }\in \mathbb{C}[{\hat{W}}_{N^{\prime }}]_{\operatorname{cusp}}$
et
![]() $\unicode[STIX]{x1D711}^{\prime \prime }\in \mathbb{C}[{\hat{W}}_{N^{\prime \prime }}]_{\operatorname{cusp}}$
. Pour un nombre réel
$\unicode[STIX]{x1D711}^{\prime \prime }\in \mathbb{C}[{\hat{W}}_{N^{\prime \prime }}]_{\operatorname{cusp}}$
. Pour un nombre réel
![]() $x$
, on note
$x$
, on note
![]() $[x]$
sa partie entière. Posons
$[x]$
sa partie entière. Posons
 $$\begin{eqnarray}\displaystyle r_{1}^{\prime } & = & \displaystyle \sup \biggl(\biggl[\frac{r^{\prime }+r^{\prime \prime }}{2}\biggr],-\biggl[\frac{r^{\prime }+r^{\prime \prime }}{2}\biggr]-1\biggr),\qquad r_{1}^{\prime \prime }=\biggl|\biggl[\frac{r^{\prime }+r^{\prime \prime }+1}{2}\biggr]\biggr|,\nonumber\\ \displaystyle r_{2}^{\prime } & = & \displaystyle \sup \biggl(\biggl[\frac{r^{\prime }-r^{\prime \prime }}{2}\biggr],-\biggl[\frac{r^{\prime }-r^{\prime \prime }}{2}\biggr]-1\biggr),\qquad r_{2}^{\prime \prime }=\biggl|\biggl[\frac{r^{\prime }-r^{\prime \prime }+1}{2}\biggr]\biggr|,\nonumber\\ \displaystyle n_{1} & = & \displaystyle r_{1}^{\prime 2}+r_{1}^{\prime }+r_{1}^{\prime \prime 2}+N^{\prime },\qquad n_{2}=r_{2}^{\prime 2}+r_{2}^{\prime }+r_{2}^{\prime \prime 2}+N^{\prime \prime },\nonumber\\ \displaystyle & & \displaystyle (N_{1}^{\prime },N_{1}^{\prime \prime })=(N^{\prime },0),\qquad (N_{2}^{\prime },N_{2}^{\prime \prime })=(N^{\prime \prime },0),\nonumber\\ \displaystyle \unicode[STIX]{x1D6FE}_{1} & = & \displaystyle (r_{1}^{\prime },r_{1}^{\prime \prime },N_{1}^{\prime },N_{1}^{\prime \prime }),\qquad \unicode[STIX]{x1D6FE}_{2}=(r_{2}^{\prime },r_{2}^{\prime \prime },N_{2}^{\prime },N_{2}^{\prime \prime }).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle r_{1}^{\prime } & = & \displaystyle \sup \biggl(\biggl[\frac{r^{\prime }+r^{\prime \prime }}{2}\biggr],-\biggl[\frac{r^{\prime }+r^{\prime \prime }}{2}\biggr]-1\biggr),\qquad r_{1}^{\prime \prime }=\biggl|\biggl[\frac{r^{\prime }+r^{\prime \prime }+1}{2}\biggr]\biggr|,\nonumber\\ \displaystyle r_{2}^{\prime } & = & \displaystyle \sup \biggl(\biggl[\frac{r^{\prime }-r^{\prime \prime }}{2}\biggr],-\biggl[\frac{r^{\prime }-r^{\prime \prime }}{2}\biggr]-1\biggr),\qquad r_{2}^{\prime \prime }=\biggl|\biggl[\frac{r^{\prime }-r^{\prime \prime }+1}{2}\biggr]\biggr|,\nonumber\\ \displaystyle n_{1} & = & \displaystyle r_{1}^{\prime 2}+r_{1}^{\prime }+r_{1}^{\prime \prime 2}+N^{\prime },\qquad n_{2}=r_{2}^{\prime 2}+r_{2}^{\prime }+r_{2}^{\prime \prime 2}+N^{\prime \prime },\nonumber\\ \displaystyle & & \displaystyle (N_{1}^{\prime },N_{1}^{\prime \prime })=(N^{\prime },0),\qquad (N_{2}^{\prime },N_{2}^{\prime \prime })=(N^{\prime \prime },0),\nonumber\\ \displaystyle \unicode[STIX]{x1D6FE}_{1} & = & \displaystyle (r_{1}^{\prime },r_{1}^{\prime \prime },N_{1}^{\prime },N_{1}^{\prime \prime }),\qquad \unicode[STIX]{x1D6FE}_{2}=(r_{2}^{\prime },r_{2}^{\prime \prime },N_{2}^{\prime },N_{2}^{\prime \prime }).\nonumber\end{eqnarray}$$
D’après la relation (2) du paragraphe 4 ci-dessous, la définition de
![]() $n_{1}$
et
$n_{1}$
et
![]() $n_{2}$
peut se récrire
$n_{2}$
peut se récrire
 $$\begin{eqnarray}\displaystyle n_{1} & = & \displaystyle \frac{(r^{\prime }+r^{\prime \prime })^{2}+(r^{\prime }+r^{\prime \prime }+1)^{2}-1}{4}+N^{\prime },\nonumber\\ \displaystyle n_{2} & = & \displaystyle \frac{(r^{\prime }-r^{\prime \prime })^{2}+(r^{\prime }-r^{\prime \prime }+1)^{2}-1}{4}+N^{\prime \prime }.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle n_{1} & = & \displaystyle \frac{(r^{\prime }+r^{\prime \prime })^{2}+(r^{\prime }+r^{\prime \prime }+1)^{2}-1}{4}+N^{\prime },\nonumber\\ \displaystyle n_{2} & = & \displaystyle \frac{(r^{\prime }-r^{\prime \prime })^{2}+(r^{\prime }-r^{\prime \prime }+1)^{2}-1}{4}+N^{\prime \prime }.\nonumber\end{eqnarray}$$
On vérifie que
![]() $(n_{1},n_{2})\in D(n)$
, que
$(n_{1},n_{2})\in D(n)$
, que
![]() $\unicode[STIX]{x1D6FE}_{1}\in \unicode[STIX]{x1D6E4}_{n_{1}}$
et
$\unicode[STIX]{x1D6FE}_{1}\in \unicode[STIX]{x1D6E4}_{n_{1}}$
et
![]() $\unicode[STIX]{x1D6FE}_{2}\in \unicode[STIX]{x1D6E4}_{n_{2}}$
. L’élément
$\unicode[STIX]{x1D6FE}_{2}\in \unicode[STIX]{x1D6E4}_{n_{2}}$
. L’élément
![]() $\unicode[STIX]{x1D711}^{\prime }$
peut être considéré comme un élément de
$\unicode[STIX]{x1D711}^{\prime }$
peut être considéré comme un élément de
![]() ${\mathcal{R}}_{\operatorname{cusp}}(\unicode[STIX]{x1D6FE}_{1})$
et l’élément
${\mathcal{R}}_{\operatorname{cusp}}(\unicode[STIX]{x1D6FE}_{1})$
et l’élément
![]() $\unicode[STIX]{x1D711}^{\prime \prime }$
peut être considéré comme un élément de
$\unicode[STIX]{x1D711}^{\prime \prime }$
peut être considéré comme un élément de
![]() ${\mathcal{R}}_{\operatorname{cusp}}(\unicode[STIX]{x1D6FE}_{2})$
. Posons
${\mathcal{R}}_{\operatorname{cusp}}(\unicode[STIX]{x1D6FE}_{2})$
. Posons
![]() $\unicode[STIX]{x1D711}=\unicode[STIX]{x1D711}^{\prime }\,\otimes \,\unicode[STIX]{x1D711}^{\prime \prime }$
. C’est un élément de
$\unicode[STIX]{x1D711}=\unicode[STIX]{x1D711}^{\prime }\,\otimes \,\unicode[STIX]{x1D711}^{\prime \prime }$
. C’est un élément de
![]() ${\mathcal{R}}_{\operatorname{cusp}}(\unicode[STIX]{x1D6FE})$
. Posons
${\mathcal{R}}_{\operatorname{cusp}}(\unicode[STIX]{x1D6FE})$
. Posons
avec les notations de [Reference Waldspurger11] 1.9, 1.10. Bien sûr, dans les deux dernières définitions, ce sont les applications
![]() $\unicode[STIX]{x1D6F9}$
,
$\unicode[STIX]{x1D6F9}$
,
![]() $k$
et
$k$
et
![]() $\unicode[STIX]{x1D70C}\unicode[STIX]{x1D704}$
relatives à
$\unicode[STIX]{x1D70C}\unicode[STIX]{x1D704}$
relatives à
![]() $n_{1}$
et
$n_{1}$
et
![]() $n_{2}$
qui interviennent.
$n_{2}$
qui interviennent.
Proposition.
(i) Sous les hypothèses ci-dessus,
 $f_{1}\,\otimes \,f_{2}$
est un transfert de
$f_{1}\,\otimes \,f_{2}$
est un transfert de
 $f$
relatif à
$f$
relatif à
 $(n_{1},n_{2})$
.
$(n_{1},n_{2})$
.(ii) Pour
 $(\bar{n}_{1},\bar{n}_{2})\in D(n)$
différent de
$(\bar{n}_{1},\bar{n}_{2})\in D(n)$
différent de
 $(n_{1},n_{2})$
, le transfert de
$(n_{1},n_{2})$
, le transfert de
 $f$
relatif à
$f$
relatif à
 $(\bar{n}_{1},\bar{n}_{2})$
est nul.
$(\bar{n}_{1},\bar{n}_{2})$
est nul.
Nous démontrerons cette proposition dans la section 3. Nous l’admettons pour la suite de la présente section.
1.3 Transfert de représentations elliptiques
Soit
![]() $(n_{1},n_{2})\in D(n)$
, auquel on associe un élément
$(n_{1},n_{2})\in D(n)$
, auquel on associe un élément
![]() $h\in \operatorname{Sp}(2n;\mathbb{C})$
tel que
$h\in \operatorname{Sp}(2n;\mathbb{C})$
tel que
![]() $h^{2}=1$
. Soit
$h^{2}=1$
. Soit
![]() $(\unicode[STIX]{x1D706}_{1},s_{1};1)\in \mathfrak{St}_{n_{1},\operatorname{unip},\operatorname{disc}}$
et
$(\unicode[STIX]{x1D706}_{1},s_{1};1)\in \mathfrak{St}_{n_{1},\operatorname{unip},\operatorname{disc}}$
et
![]() $(\unicode[STIX]{x1D706}_{2},s_{2},1)\in \mathfrak{St}_{n_{2},\operatorname{unip},\operatorname{disc}}$
, cf. [Reference Waldspurger11] 2.4. Comme en [Reference Waldspurger11] 2.1, on associe à ces données un triplet
$(\unicode[STIX]{x1D706}_{2},s_{2},1)\in \mathfrak{St}_{n_{2},\operatorname{unip},\operatorname{disc}}$
, cf. [Reference Waldspurger11] 2.4. Comme en [Reference Waldspurger11] 2.1, on associe à ces données un triplet
![]() $(\unicode[STIX]{x1D706},s,h)\in \mathfrak{Endo}_{\operatorname{unip}\!{-}\!\operatorname{disc}}$
.
$(\unicode[STIX]{x1D706},s,h)\in \mathfrak{Endo}_{\operatorname{unip}\!{-}\!\operatorname{disc}}$
.
Théorème. On a les égalités
Preuve.
Notons respectivement
![]() $\unicode[STIX]{x1D6E9}_{1,\operatorname{iso}}$
,
$\unicode[STIX]{x1D6E9}_{1,\operatorname{iso}}$
,
![]() $\unicode[STIX]{x1D6E9}_{1,\operatorname{an}}$
,
$\unicode[STIX]{x1D6E9}_{1,\operatorname{an}}$
,
![]() $\unicode[STIX]{x1D6E9}_{2,\operatorname{iso}}$
,
$\unicode[STIX]{x1D6E9}_{2,\operatorname{iso}}$
,
![]() $\unicode[STIX]{x1D6E9}_{2,\operatorname{an}}$
,
$\unicode[STIX]{x1D6E9}_{2,\operatorname{an}}$
,
![]() $\unicode[STIX]{x1D6E9}_{\operatorname{iso}}$
et
$\unicode[STIX]{x1D6E9}_{\operatorname{iso}}$
et
![]() $\unicode[STIX]{x1D6E9}_{\operatorname{an}}$
les caractères-fonctions des représentations
$\unicode[STIX]{x1D6E9}_{\operatorname{an}}$
les caractères-fonctions des représentations
![]() $\unicode[STIX]{x1D6F1}_{\operatorname{iso}}(\unicode[STIX]{x1D706}_{1},s_{1},1)$
,
$\unicode[STIX]{x1D6F1}_{\operatorname{iso}}(\unicode[STIX]{x1D706}_{1},s_{1},1)$
,
![]() $\unicode[STIX]{x1D6F1}_{\operatorname{an}}(\unicode[STIX]{x1D706}_{1},s_{1},1)$
,
$\unicode[STIX]{x1D6F1}_{\operatorname{an}}(\unicode[STIX]{x1D706}_{1},s_{1},1)$
,
![]() $\unicode[STIX]{x1D6F1}_{\operatorname{iso}}(\unicode[STIX]{x1D706}_{2},s_{2},1)$
,
$\unicode[STIX]{x1D6F1}_{\operatorname{iso}}(\unicode[STIX]{x1D706}_{2},s_{2},1)$
,
![]() $\unicode[STIX]{x1D6F1}_{\operatorname{an}}(\unicode[STIX]{x1D706}_{2},s_{2},1)$
,
$\unicode[STIX]{x1D6F1}_{\operatorname{an}}(\unicode[STIX]{x1D706}_{2},s_{2},1)$
,
![]() $\unicode[STIX]{x1D6F1}_{\operatorname{iso}}(\unicode[STIX]{x1D706},s,h)$
et
$\unicode[STIX]{x1D6F1}_{\operatorname{iso}}(\unicode[STIX]{x1D706},s,h)$
et
![]() $\unicode[STIX]{x1D6F1}_{\operatorname{an}}(\unicode[STIX]{x1D706},s,h)$
. Les égalités à démontrer se traduisent par des égalités entre ces caractères. Toutes les représentations intervenant sont elliptiques. D’après [Reference Arthur2] théorème 6.2, il suffit donc de démontrer ces égalités restreintes aux éléments elliptiques des différents groupes. Écrivons ces égalités. Posons
$\unicode[STIX]{x1D6F1}_{\operatorname{an}}(\unicode[STIX]{x1D706},s,h)$
. Les égalités à démontrer se traduisent par des égalités entre ces caractères. Toutes les représentations intervenant sont elliptiques. D’après [Reference Arthur2] théorème 6.2, il suffit donc de démontrer ces égalités restreintes aux éléments elliptiques des différents groupes. Écrivons ces égalités. Posons
![]() $\operatorname{sgn}_{\operatorname{iso}}=1$
et
$\operatorname{sgn}_{\operatorname{iso}}=1$
et
![]() $\operatorname{sgn}_{\operatorname{an}}=-1$
. Pour
$\operatorname{sgn}_{\operatorname{an}}=-1$
. Pour
![]() $\sharp =\operatorname{iso}$
ou
$\sharp =\operatorname{iso}$
ou
![]() $\operatorname{an}$
et pour
$\operatorname{an}$
et pour
![]() $x\in G_{\sharp }(F)$
fortement régulier et elliptique, on doit avoir
$x\in G_{\sharp }(F)$
fortement régulier et elliptique, on doit avoir
 $$\begin{eqnarray}\displaystyle & & \displaystyle D^{G_{\sharp }}(x)^{1/2}\unicode[STIX]{x1D6E9}_{\sharp }(x)\nonumber\\ \displaystyle & & \displaystyle \quad =\operatorname{sgn}_{\sharp }\mathop{\sum }_{x_{1},x_{2}}D^{G_{n_{1},\operatorname{iso}}}(x_{1})^{1/2}D^{G_{n_{2},\operatorname{iso}}}(x_{2})^{1/2}\unicode[STIX]{x1D6E5}_{h}((x_{1},x_{2}),x)\nonumber\\ \displaystyle & & \displaystyle \qquad \times \,\unicode[STIX]{x1D6E9}_{1,\operatorname{iso}}(x_{1})\unicode[STIX]{x1D6E9}_{2,\operatorname{iso}}(x_{2}),\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle D^{G_{\sharp }}(x)^{1/2}\unicode[STIX]{x1D6E9}_{\sharp }(x)\nonumber\\ \displaystyle & & \displaystyle \quad =\operatorname{sgn}_{\sharp }\mathop{\sum }_{x_{1},x_{2}}D^{G_{n_{1},\operatorname{iso}}}(x_{1})^{1/2}D^{G_{n_{2},\operatorname{iso}}}(x_{2})^{1/2}\unicode[STIX]{x1D6E5}_{h}((x_{1},x_{2}),x)\nonumber\\ \displaystyle & & \displaystyle \qquad \times \,\unicode[STIX]{x1D6E9}_{1,\operatorname{iso}}(x_{1})\unicode[STIX]{x1D6E9}_{2,\operatorname{iso}}(x_{2}),\end{eqnarray}$$
où
![]() $x_{1}$
, respectivement
$x_{1}$
, respectivement
![]() $x_{2}$
, parcourt les éléments fortement réguliers et elliptiques de
$x_{2}$
, parcourt les éléments fortement réguliers et elliptiques de
![]() $G_{n_{1},\operatorname{iso}}(F)$
, respectivement
$G_{n_{1},\operatorname{iso}}(F)$
, respectivement
![]() $G_{n_{2},\operatorname{iso}}(F)$
, à conjugaison stable près. Ici encore, on peut se limiter aux couples
$G_{n_{2},\operatorname{iso}}(F)$
, à conjugaison stable près. Ici encore, on peut se limiter aux couples
![]() $(x_{1},x_{2})$
correspondant par endoscopie à la classe de conjugaison stable de
$(x_{1},x_{2})$
correspondant par endoscopie à la classe de conjugaison stable de
![]() $x$
. La somme est finie.
$x$
. La somme est finie.
Posons
![]() $f_{1}=\unicode[STIX]{x1D6F9}\circ \operatorname{proj}_{\operatorname{cusp}}\circ \operatorname{Res}\circ D\circ \unicode[STIX]{x1D6F1}(\unicode[STIX]{x1D706}_{1},s_{1},1)$
,
$f_{1}=\unicode[STIX]{x1D6F9}\circ \operatorname{proj}_{\operatorname{cusp}}\circ \operatorname{Res}\circ D\circ \unicode[STIX]{x1D6F1}(\unicode[STIX]{x1D706}_{1},s_{1},1)$
,
![]() $f_{2}=\unicode[STIX]{x1D6F9}\circ \operatorname{proj}_{\operatorname{cusp}}\circ \operatorname{Res}\circ D\circ \unicode[STIX]{x1D6F1}(\unicode[STIX]{x1D706}_{2},s_{2},1)$
,
$f_{2}=\unicode[STIX]{x1D6F9}\circ \operatorname{proj}_{\operatorname{cusp}}\circ \operatorname{Res}\circ D\circ \unicode[STIX]{x1D6F1}(\unicode[STIX]{x1D706}_{2},s_{2},1)$
,
![]() $f=\unicode[STIX]{x1D6F9}\circ \operatorname{proj}_{\operatorname{cusp}}\circ \operatorname{Res}\circ D\circ \unicode[STIX]{x1D6F1}(\unicode[STIX]{x1D706},s,h)$
. Pour
$f=\unicode[STIX]{x1D6F9}\circ \operatorname{proj}_{\operatorname{cusp}}\circ \operatorname{Res}\circ D\circ \unicode[STIX]{x1D6F1}(\unicode[STIX]{x1D706},s,h)$
. Pour
![]() $\sharp =\operatorname{iso}$
ou
$\sharp =\operatorname{iso}$
ou
![]() $\operatorname{an}$
, on a l’égalité
$\operatorname{an}$
, on a l’égalité
![]() $\operatorname{proj}_{\operatorname{cusp}}\circ \operatorname{Res}\circ D\circ \unicode[STIX]{x1D6F1}_{\sharp }(\unicode[STIX]{x1D706},s,h)=(-1)^{n}\operatorname{sgn}_{\sharp }\operatorname{proj}_{\operatorname{cusp}}\circ \operatorname{Res}\circ \unicode[STIX]{x1D6F1}_{\sharp }(\unicode[STIX]{x1D706},s,h)$
, cf. [Reference Moeglin and Waldspurger6] corollaire 5.7. D’après la proposition 1.1, on a donc l’égalité
$\operatorname{proj}_{\operatorname{cusp}}\circ \operatorname{Res}\circ D\circ \unicode[STIX]{x1D6F1}_{\sharp }(\unicode[STIX]{x1D706},s,h)=(-1)^{n}\operatorname{sgn}_{\sharp }\operatorname{proj}_{\operatorname{cusp}}\circ \operatorname{Res}\circ \unicode[STIX]{x1D6F1}_{\sharp }(\unicode[STIX]{x1D706},s,h)$
, cf. [Reference Moeglin and Waldspurger6] corollaire 5.7. D’après la proposition 1.1, on a donc l’égalité
On a des égalités analogues pour
![]() $\unicode[STIX]{x1D6E9}_{1}(x_{1})$
et
$\unicode[STIX]{x1D6E9}_{1}(x_{1})$
et
![]() $\unicode[STIX]{x1D6E9}_{2}(x_{2})$
. Ces dernières égalités entraînent
$\unicode[STIX]{x1D6E9}_{2}(x_{2})$
. Ces dernières égalités entraînent
(2) soit
![]() $j=1,2$
,
$j=1,2$
,
![]() $\sharp _{j}=\operatorname{iso}$
ou
$\sharp _{j}=\operatorname{iso}$
ou
![]() $\operatorname{an}$
,
$\operatorname{an}$
,
![]() $x_{j}\in G_{n_{j},\operatorname{iso}}(F)$
et
$x_{j}\in G_{n_{j},\operatorname{iso}}(F)$
et
![]() $y_{j}\in G_{n_{j},\sharp _{j}}(F)$
; supposons que
$y_{j}\in G_{n_{j},\sharp _{j}}(F)$
; supposons que
![]() $x_{j}$
et
$x_{j}$
et
![]() $y_{j}$
sont fortement réguliers et elliptiques et que leurs classes de conjugaison stable sont égales si
$y_{j}$
sont fortement réguliers et elliptiques et que leurs classes de conjugaison stable sont égales si
![]() $\sharp _{j}=\operatorname{iso}$
ou se correspondent si
$\sharp _{j}=\operatorname{iso}$
ou se correspondent si
![]() $\sharp _{j}=\operatorname{an}$
, alors
$\sharp _{j}=\operatorname{an}$
, alors
![]() $J(x_{j},f_{j})=J(y_{j},f_{j})$
.
$J(x_{j},f_{j})=J(y_{j},f_{j})$
.
Cela traduit le fait que
![]() $\unicode[STIX]{x1D6E9}_{j,\operatorname{iso}}$
est stable et que
$\unicode[STIX]{x1D6E9}_{j,\operatorname{iso}}$
est stable et que
![]() $-\unicode[STIX]{x1D6E9}_{j,\operatorname{an}}$
en est son transfert, cf. [Reference Waldspurger11] 2.1.
$-\unicode[STIX]{x1D6E9}_{j,\operatorname{an}}$
en est son transfert, cf. [Reference Waldspurger11] 2.1.
Parce que les facteurs de transfert valent
![]() $\pm 1$
et sont donc à valeurs réelles, l’égalité (1) se récrit
$\pm 1$
et sont donc à valeurs réelles, l’égalité (1) se récrit
pour tout
![]() $x\in G_{\operatorname{iso}}(F)\cup G_{\operatorname{an}}(F)$
fortement régulier et elliptique.
$x\in G_{\operatorname{iso}}(F)\cup G_{\operatorname{an}}(F)$
fortement régulier et elliptique.
La propriété de base de l’endoscopie est que les intégrales orbitales
![]() $J(x,f)$
sont déterminées par les intégrales endoscopiques
$J(x,f)$
sont déterminées par les intégrales endoscopiques
![]() $J^{\operatorname{endo}}(\bar{x}_{1},\bar{x}_{2},f)$
quand
$J^{\operatorname{endo}}(\bar{x}_{1},\bar{x}_{2},f)$
quand
![]() $(\bar{n}_{1},\bar{n}_{2})$
décrit
$(\bar{n}_{1},\bar{n}_{2})$
décrit
![]() $D(n)$
et
$D(n)$
et
![]() $(\bar{x}_{1},\bar{x}_{2})\in G_{\bar{n}_{1},\operatorname{iso}}(F)\times G_{\bar{n}_{2},\operatorname{iso}}(F)$
décrit les couples
$(\bar{x}_{1},\bar{x}_{2})\in G_{\bar{n}_{1},\operatorname{iso}}(F)\times G_{\bar{n}_{2},\operatorname{iso}}(F)$
décrit les couples
![]() $n$
-réguliers formés d’éléments elliptiques. Donc (3) équivaut, pour toutes données
$n$
-réguliers formés d’éléments elliptiques. Donc (3) équivaut, pour toutes données
![]() $(\bar{n}_{1},\bar{n}_{2})$
et
$(\bar{n}_{1},\bar{n}_{2})$
et
![]() $(\bar{x}_{1},\bar{x}_{2})$
comme ci-dessus, à ce que l’on ait l’égalité
$(\bar{x}_{1},\bar{x}_{2})$
comme ci-dessus, à ce que l’on ait l’égalité
 $$\begin{eqnarray}\displaystyle J^{\operatorname{endo}}(\bar{x}_{1},\bar{x}_{2},f) & = & \displaystyle \mathop{\sum }_{x}\unicode[STIX]{x1D6E5}_{\bar{h}}((\bar{x}_{1},\bar{x}_{2}),x)J(x,f)\nonumber\\ \displaystyle & = & \displaystyle \mathop{\sum }_{x}\unicode[STIX]{x1D6E5}_{\bar{h}}((\bar{x}_{1},\bar{x}_{2}),x)\!\mathop{\sum }_{x_{1},x_{2}}\!\unicode[STIX]{x1D6E5}_{h}((x_{1},x_{2}),x)J(x_{1},f_{1})J(x_{2},f_{2}),\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle J^{\operatorname{endo}}(\bar{x}_{1},\bar{x}_{2},f) & = & \displaystyle \mathop{\sum }_{x}\unicode[STIX]{x1D6E5}_{\bar{h}}((\bar{x}_{1},\bar{x}_{2}),x)J(x,f)\nonumber\\ \displaystyle & = & \displaystyle \mathop{\sum }_{x}\unicode[STIX]{x1D6E5}_{\bar{h}}((\bar{x}_{1},\bar{x}_{2}),x)\!\mathop{\sum }_{x_{1},x_{2}}\!\unicode[STIX]{x1D6E5}_{h}((x_{1},x_{2}),x)J(x_{1},f_{1})J(x_{2},f_{2}),\nonumber\end{eqnarray}$$
où l’on somme sur les éléments
![]() $x\in G_{\operatorname{iso}}(F)\cup G_{\operatorname{an}}(F)$
fortement réguliers et elliptiques modulo conjugaison. On a noté
$x\in G_{\operatorname{iso}}(F)\cup G_{\operatorname{an}}(F)$
fortement réguliers et elliptiques modulo conjugaison. On a noté
![]() $\bar{h}$
l’élément de
$\bar{h}$
l’élément de
![]() $\operatorname{Sp}(2n;\mathbb{C})$
tel que
$\operatorname{Sp}(2n;\mathbb{C})$
tel que
![]() $\bar{h}^{2}=1$
associé à
$\bar{h}^{2}=1$
associé à
![]() $(\bar{n}_{1},\bar{n}_{2})$
. On récrit l’égalité ci-dessus :
$(\bar{n}_{1},\bar{n}_{2})$
. On récrit l’égalité ci-dessus :
La somme intérieure en
![]() $x$
est nulle sauf si
$x$
est nulle sauf si
![]() $(\bar{n}_{1},\bar{n}_{2})=(n_{1},n_{2})$
et, à conjugaison stable près,
$(\bar{n}_{1},\bar{n}_{2})=(n_{1},n_{2})$
et, à conjugaison stable près,
![]() $(\bar{x}_{1},\bar{x}_{2})=(x_{1},x_{2})$
. Si ces conditions sont vérifiées, la somme vaut le nombre de
$(\bar{x}_{1},\bar{x}_{2})=(x_{1},x_{2})$
. Si ces conditions sont vérifiées, la somme vaut le nombre de
![]() $x$
, pris à conjugaison près, qui interviennent dans la somme. C’est le nombre
$x$
, pris à conjugaison près, qui interviennent dans la somme. C’est le nombre
![]() $z(x)$
défini en 1.2 pour un quelconque de ces
$z(x)$
défini en 1.2 pour un quelconque de ces
![]() $x$
. Or on vérifie facilement l’égalité
$x$
. Or on vérifie facilement l’égalité
![]() $z(x)=z(\bar{x}_{1})z(\bar{x}_{2})$
. Dans le cas où
$z(x)=z(\bar{x}_{1})z(\bar{x}_{2})$
. Dans le cas où
![]() $(\bar{n}_{1},\bar{n}_{2})=(n_{1},n_{2})$
, on obtient donc
$(\bar{n}_{1},\bar{n}_{2})=(n_{1},n_{2})$
, on obtient donc
Mais la propriété (2) entraîne que, pour
![]() $j=1,2$
,
$j=1,2$
,
![]() $z(\bar{x}_{j})J(\bar{x}_{j},f_{j})=S(\bar{x}_{j},f_{j})$
. L’égalité ci-dessus se transforme en
$z(\bar{x}_{j})J(\bar{x}_{j},f_{j})=S(\bar{x}_{j},f_{j})$
. L’égalité ci-dessus se transforme en
Autrement dit,
![]() $f_{1}\,\otimes \,f_{2}$
est un transfert de
$f_{1}\,\otimes \,f_{2}$
est un transfert de
![]() $f$
. Résumons : l’égalité (3) équivaut aux assertions
$f$
. Résumons : l’égalité (3) équivaut aux assertions
(4)(a)
![]() $f_{1}\,\otimes \,f_{2}$
est un transfert de
$f_{1}\,\otimes \,f_{2}$
est un transfert de
![]() $f$
relatif à
$f$
relatif à
![]() $(n_{1},n_{2})$
;
$(n_{1},n_{2})$
;
(4)(b) pour
![]() $(\bar{n}_{1},\bar{n}_{2})\in D(n)$
différent de
$(\bar{n}_{1},\bar{n}_{2})\in D(n)$
différent de
![]() $(n_{1},n_{2})$
, le transfert de
$(n_{1},n_{2})$
, le transfert de
![]() $f$
relatif à
$f$
relatif à
![]() $(\bar{n}_{1},\bar{n}_{2})$
est nul.
$(\bar{n}_{1},\bar{n}_{2})$
est nul.
Calculons
![]() $f$
. D’après le lemme 2.3 de [Reference Waldspurger11] et parce que
$f$
. D’après le lemme 2.3 de [Reference Waldspurger11] et parce que
![]() ${\mathcal{F}}^{\operatorname{par}}$
est une involution, on a
${\mathcal{F}}^{\operatorname{par}}$
est une involution, on a
![]() $\operatorname{proj}_{\operatorname{cusp}}={\mathcal{F}}^{\operatorname{par}}\circ \operatorname{proj}_{\operatorname{cusp}}\circ \,\mathfrak{F}^{\operatorname{par}}$
. Par définition de
$\operatorname{proj}_{\operatorname{cusp}}={\mathcal{F}}^{\operatorname{par}}\circ \operatorname{proj}_{\operatorname{cusp}}\circ \,\mathfrak{F}^{\operatorname{par}}$
. Par définition de
![]() $\mathfrak{F}^{\operatorname{par}}$
, on a aussi
$\mathfrak{F}^{\operatorname{par}}$
, on a aussi
![]() $\mathfrak{F}^{\operatorname{par}}\circ \operatorname{Res}\circ D=\operatorname{Res}\circ D\circ {\mathcal{F}}$
. D’où
$\mathfrak{F}^{\operatorname{par}}\circ \operatorname{Res}\circ D=\operatorname{Res}\circ D\circ {\mathcal{F}}$
. D’où
La décomposition de
![]() $\unicode[STIX]{x1D706}$
associée à
$\unicode[STIX]{x1D706}$
associée à
![]() $h$
est
$h$
est
![]() $\unicode[STIX]{x1D706}=\unicode[STIX]{x1D706}_{1}\cup \unicode[STIX]{x1D706}_{2}$
. Il résulte des définitions que
$\unicode[STIX]{x1D706}=\unicode[STIX]{x1D706}_{1}\cup \unicode[STIX]{x1D706}_{2}$
. Il résulte des définitions que
où
![]() $(\unicode[STIX]{x1D716}_{1},\unicode[STIX]{x1D716}_{2})$
parcourt
$(\unicode[STIX]{x1D716}_{1},\unicode[STIX]{x1D716}_{2})$
parcourt
![]() $\{\pm 1\}^{\operatorname{Jord}_{\text{bp}}(\unicode[STIX]{x1D706}_{1})}\times \{\pm 1\}^{\operatorname{Jord}_{\text{bp}}(\unicode[STIX]{x1D706}_{2})}$
et les termes
$\{\pm 1\}^{\operatorname{Jord}_{\text{bp}}(\unicode[STIX]{x1D706}_{1})}\times \{\pm 1\}^{\operatorname{Jord}_{\text{bp}}(\unicode[STIX]{x1D706}_{2})}$
et les termes
![]() $\unicode[STIX]{x1D716}_{1}(s_{1})$
et
$\unicode[STIX]{x1D716}_{1}(s_{1})$
et
![]() $\unicode[STIX]{x1D716}_{2}(s_{2})$
sont définis en interprétant
$\unicode[STIX]{x1D716}_{2}(s_{2})$
sont définis en interprétant
![]() $\unicode[STIX]{x1D716}_{1}$
et
$\unicode[STIX]{x1D716}_{1}$
et
![]() $\unicode[STIX]{x1D716}_{2}$
comme des éléments de
$\unicode[STIX]{x1D716}_{2}$
comme des éléments de
![]() $\mathbf{Z}(\unicode[STIX]{x1D706}_{1},1)^{\vee }$
et
$\mathbf{Z}(\unicode[STIX]{x1D706}_{1},1)^{\vee }$
et
![]() $\mathbf{Z}(\unicode[STIX]{x1D706}_{2},1)^{\vee }$
, cf. [Reference Waldspurger11] 1.3. La proposition [Reference Waldspurger11] 1.11 calcule
$\mathbf{Z}(\unicode[STIX]{x1D706}_{2},1)^{\vee }$
, cf. [Reference Waldspurger11] 1.3. La proposition [Reference Waldspurger11] 1.11 calcule
![]() $\operatorname{Res}\circ D(\unicode[STIX]{x1D70B}(\unicode[STIX]{x1D706}_{1},\unicode[STIX]{x1D716}_{1},\unicode[STIX]{x1D706}_{2},\unicode[STIX]{x1D716}_{2}))$
.
$\operatorname{Res}\circ D(\unicode[STIX]{x1D70B}(\unicode[STIX]{x1D706}_{1},\unicode[STIX]{x1D716}_{1},\unicode[STIX]{x1D706}_{2},\unicode[STIX]{x1D716}_{2}))$
.
Changement de notations. Dans la formule de cette proposition figure un isomorphisme
![]() $j$
entre deux espaces, l’un d’eux étant l’espace
$j$
entre deux espaces, l’un d’eux étant l’espace
![]() ${\mathcal{R}}$
. Distinguer ces deux espaces nous a été utile dans la deuxième section de [Reference Waldspurger11]. Maintenant, cela ne nous sert plus. Pour simplifier, on identifie par
${\mathcal{R}}$
. Distinguer ces deux espaces nous a été utile dans la deuxième section de [Reference Waldspurger11]. Maintenant, cela ne nous sert plus. Pour simplifier, on identifie par
![]() $j$
les deux espaces en question et on fait disparaître
$j$
les deux espaces en question et on fait disparaître
![]() $j$
de la notation.
$j$
de la notation.
On obtient
Les applications
![]() $\text{Rep}$
,
$\text{Rep}$
,
![]() $k$
,
$k$
,
![]() ${\mathcal{F}}^{\operatorname{par}}$
et
${\mathcal{F}}^{\operatorname{par}}$
et
![]() $\unicode[STIX]{x1D70C}\unicode[STIX]{x1D704}$
commutent aux projections cuspidales. De plus,
$\unicode[STIX]{x1D70C}\unicode[STIX]{x1D704}$
commutent aux projections cuspidales. De plus,
![]() ${\mathcal{F}}^{\operatorname{par}}\circ \text{Rep}=k$
. Il en résulte que
${\mathcal{F}}^{\operatorname{par}}\circ \text{Rep}=k$
. Il en résulte que
Un calcul analogue s’applique à
![]() $f_{1}$
et
$f_{1}$
et
![]() $f_{2}$
. On a cette fois
$f_{2}$
. On a cette fois
![]() ${\mathcal{F}}(\unicode[STIX]{x1D706}_{j},s_{j},1)=(\unicode[STIX]{x1D706}_{j},1,s_{j})$
pour
${\mathcal{F}}(\unicode[STIX]{x1D706}_{j},s_{j},1)=(\unicode[STIX]{x1D706}_{j},1,s_{j})$
pour
![]() $j=1,2$
et la décomposition de
$j=1,2$
et la décomposition de
![]() $\unicode[STIX]{x1D706}_{j}$
associée à
$\unicode[STIX]{x1D706}_{j}$
associée à
![]() $1$
est
$1$
est
![]() $\unicode[STIX]{x1D706}_{j}=\unicode[STIX]{x1D706}_{j}\cup \emptyset$
. Autrement dit, les secondes composantes de la formule ci-dessus disparaissent. On obtient
$\unicode[STIX]{x1D706}_{j}=\unicode[STIX]{x1D706}_{j}\cup \emptyset$
. Autrement dit, les secondes composantes de la formule ci-dessus disparaissent. On obtient
 $$\begin{eqnarray}\displaystyle f_{1} & = & \displaystyle \mathop{\sum }_{\unicode[STIX]{x1D716}_{1}}\unicode[STIX]{x1D716}_{1}(s_{1})\unicode[STIX]{x1D6F9}\circ k\circ \unicode[STIX]{x1D70C}\unicode[STIX]{x1D704}\circ \operatorname{proj}_{\operatorname{cusp}}(\boldsymbol{\unicode[STIX]{x1D70C}}_{\unicode[STIX]{x1D706}_{1},\unicode[STIX]{x1D716}_{1}}),\nonumber\\ \displaystyle f_{2} & = & \displaystyle \mathop{\sum }_{\unicode[STIX]{x1D716}_{2}}\unicode[STIX]{x1D716}_{2}(s_{2})\unicode[STIX]{x1D6F9}\circ k\circ \unicode[STIX]{x1D70C}\unicode[STIX]{x1D704}\circ \operatorname{proj}_{\operatorname{cusp}}(\boldsymbol{\unicode[STIX]{x1D70C}}_{\unicode[STIX]{x1D706}_{2},\unicode[STIX]{x1D716}_{2}}),\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle f_{1} & = & \displaystyle \mathop{\sum }_{\unicode[STIX]{x1D716}_{1}}\unicode[STIX]{x1D716}_{1}(s_{1})\unicode[STIX]{x1D6F9}\circ k\circ \unicode[STIX]{x1D70C}\unicode[STIX]{x1D704}\circ \operatorname{proj}_{\operatorname{cusp}}(\boldsymbol{\unicode[STIX]{x1D70C}}_{\unicode[STIX]{x1D706}_{1},\unicode[STIX]{x1D716}_{1}}),\nonumber\\ \displaystyle f_{2} & = & \displaystyle \mathop{\sum }_{\unicode[STIX]{x1D716}_{2}}\unicode[STIX]{x1D716}_{2}(s_{2})\unicode[STIX]{x1D6F9}\circ k\circ \unicode[STIX]{x1D70C}\unicode[STIX]{x1D704}\circ \operatorname{proj}_{\operatorname{cusp}}(\boldsymbol{\unicode[STIX]{x1D70C}}_{\unicode[STIX]{x1D706}_{2},\unicode[STIX]{x1D716}_{2}}),\nonumber\end{eqnarray}$$
où les représentations
![]() $\boldsymbol{\unicode[STIX]{x1D70C}}_{\unicode[STIX]{x1D706}_{1},\unicode[STIX]{x1D716}_{2}}$
et
$\boldsymbol{\unicode[STIX]{x1D70C}}_{\unicode[STIX]{x1D706}_{1},\unicode[STIX]{x1D716}_{2}}$
et
![]() $\boldsymbol{\unicode[STIX]{x1D70C}}_{\unicode[STIX]{x1D706}_{2},\unicode[STIX]{x1D716}_{2}}$
sont assimilées à des produits tensoriels dont le second terme est trivial. Pour
$\boldsymbol{\unicode[STIX]{x1D70C}}_{\unicode[STIX]{x1D706}_{2},\unicode[STIX]{x1D716}_{2}}$
sont assimilées à des produits tensoriels dont le second terme est trivial. Pour
![]() $(\unicode[STIX]{x1D716}_{1},\unicode[STIX]{x1D716}_{2})\in \{\pm 1\}^{\operatorname{Jord}_{\text{bp}}(\unicode[STIX]{x1D706}_{1})}\times \{\pm 1\}^{\operatorname{Jord}_{\text{bp}}(\unicode[STIX]{x1D706}_{2})}$
, posons
$(\unicode[STIX]{x1D716}_{1},\unicode[STIX]{x1D716}_{2})\in \{\pm 1\}^{\operatorname{Jord}_{\text{bp}}(\unicode[STIX]{x1D706}_{1})}\times \{\pm 1\}^{\operatorname{Jord}_{\text{bp}}(\unicode[STIX]{x1D706}_{2})}$
, posons
 $$\begin{eqnarray}\displaystyle f_{\unicode[STIX]{x1D716}_{1},\unicode[STIX]{x1D716}_{2}} & = & \displaystyle \unicode[STIX]{x1D6F9}\circ k\circ \operatorname{proj}_{\operatorname{cusp}}(\boldsymbol{\unicode[STIX]{x1D70C}}_{\unicode[STIX]{x1D706}_{1},\unicode[STIX]{x1D716}_{1}}\,\otimes \,\boldsymbol{\unicode[STIX]{x1D70C}}_{\unicode[STIX]{x1D706}_{2},\unicode[STIX]{x1D716}_{2}}),\nonumber\\ \displaystyle f_{\unicode[STIX]{x1D716}_{1}} & = & \displaystyle \unicode[STIX]{x1D6F9}\circ k\circ \operatorname{proj}_{\operatorname{cusp}}(\boldsymbol{\unicode[STIX]{x1D70C}}_{\unicode[STIX]{x1D706}_{1},\unicode[STIX]{x1D716}_{1}}),\nonumber\\ \displaystyle f_{\unicode[STIX]{x1D716}_{2}} & = & \displaystyle \unicode[STIX]{x1D6F9}\circ k\circ \operatorname{proj}_{\operatorname{cusp}}(\boldsymbol{\unicode[STIX]{x1D70C}}_{\unicode[STIX]{x1D706}_{2},\unicode[STIX]{x1D716}_{2}}).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle f_{\unicode[STIX]{x1D716}_{1},\unicode[STIX]{x1D716}_{2}} & = & \displaystyle \unicode[STIX]{x1D6F9}\circ k\circ \operatorname{proj}_{\operatorname{cusp}}(\boldsymbol{\unicode[STIX]{x1D70C}}_{\unicode[STIX]{x1D706}_{1},\unicode[STIX]{x1D716}_{1}}\,\otimes \,\boldsymbol{\unicode[STIX]{x1D70C}}_{\unicode[STIX]{x1D706}_{2},\unicode[STIX]{x1D716}_{2}}),\nonumber\\ \displaystyle f_{\unicode[STIX]{x1D716}_{1}} & = & \displaystyle \unicode[STIX]{x1D6F9}\circ k\circ \operatorname{proj}_{\operatorname{cusp}}(\boldsymbol{\unicode[STIX]{x1D70C}}_{\unicode[STIX]{x1D706}_{1},\unicode[STIX]{x1D716}_{1}}),\nonumber\\ \displaystyle f_{\unicode[STIX]{x1D716}_{2}} & = & \displaystyle \unicode[STIX]{x1D6F9}\circ k\circ \operatorname{proj}_{\operatorname{cusp}}(\boldsymbol{\unicode[STIX]{x1D70C}}_{\unicode[STIX]{x1D706}_{2},\unicode[STIX]{x1D716}_{2}}).\nonumber\end{eqnarray}$$
Les propriétés (4) résultent des propriétés suivantes, pour tout
![]() $(\unicode[STIX]{x1D716}_{1},\unicode[STIX]{x1D716}_{2})$
:
$(\unicode[STIX]{x1D716}_{1},\unicode[STIX]{x1D716}_{2})$
:
(5)(a)
![]() $f_{\unicode[STIX]{x1D716}_{1}}\,\otimes \,f_{\unicode[STIX]{x1D716}_{2}}$
est un transfert de
$f_{\unicode[STIX]{x1D716}_{1}}\,\otimes \,f_{\unicode[STIX]{x1D716}_{2}}$
est un transfert de
![]() $f_{\unicode[STIX]{x1D716}_{1},\unicode[STIX]{x1D716}_{2}}$
relatif à
$f_{\unicode[STIX]{x1D716}_{1},\unicode[STIX]{x1D716}_{2}}$
relatif à
![]() $(n_{1},n_{2})$
;
$(n_{1},n_{2})$
;
(5)(b) pour
![]() $(\bar{n}_{1},\bar{n}_{2})\in D(n)$
différent de
$(\bar{n}_{1},\bar{n}_{2})\in D(n)$
différent de
![]() $(n_{1},n_{2})$
, le transfert de
$(n_{1},n_{2})$
, le transfert de
![]() $f_{\unicode[STIX]{x1D716}_{1},\unicode[STIX]{x1D716}_{2}}$
relatif à
$f_{\unicode[STIX]{x1D716}_{1},\unicode[STIX]{x1D716}_{2}}$
relatif à
![]() $(\bar{n}_{1},\bar{n}_{2})$
est nul.
$(\bar{n}_{1},\bar{n}_{2})$
est nul.
Fixons
![]() $\unicode[STIX]{x1D716}_{1}$
et
$\unicode[STIX]{x1D716}_{1}$
et
![]() $\unicode[STIX]{x1D716}_{2}$
. À
$\unicode[STIX]{x1D716}_{2}$
. À
![]() $(\unicode[STIX]{x1D706}_{1},\unicode[STIX]{x1D716}_{1})$
et
$(\unicode[STIX]{x1D706}_{1},\unicode[STIX]{x1D716}_{1})$
et
![]() $(\unicode[STIX]{x1D706}_{2},\unicode[STIX]{x1D716}_{2})$
sont associés des couples
$(\unicode[STIX]{x1D706}_{2},\unicode[STIX]{x1D716}_{2})$
sont associés des couples
![]() $(k_{1},N_{1})$
et
$(k_{1},N_{1})$
et
![]() $(k_{2},N_{2})$
, puis un triplet
$(k_{2},N_{2})$
, puis un triplet
![]() $\unicode[STIX]{x1D6FE}=(r^{\prime },r^{\prime \prime },N_{1},N_{2})\in \unicode[STIX]{x1D6E4}$
, cf. [Reference Waldspurger11] 1.11. L’élément
$\unicode[STIX]{x1D6FE}=(r^{\prime },r^{\prime \prime },N_{1},N_{2})\in \unicode[STIX]{x1D6E4}$
, cf. [Reference Waldspurger11] 1.11. L’élément
![]() $\operatorname{proj}_{\operatorname{cusp}}(\boldsymbol{\unicode[STIX]{x1D70C}}_{\unicode[STIX]{x1D706}_{1},\unicode[STIX]{x1D716}_{1}}\,\otimes \,\boldsymbol{\unicode[STIX]{x1D70C}}_{\unicode[STIX]{x1D706}_{2},\unicode[STIX]{x1D716}_{2}})$
appartient à
$\operatorname{proj}_{\operatorname{cusp}}(\boldsymbol{\unicode[STIX]{x1D70C}}_{\unicode[STIX]{x1D706}_{1},\unicode[STIX]{x1D716}_{1}}\,\otimes \,\boldsymbol{\unicode[STIX]{x1D70C}}_{\unicode[STIX]{x1D706}_{2},\unicode[STIX]{x1D716}_{2}})$
appartient à
![]() ${\mathcal{R}}_{\operatorname{cusp}}(\unicode[STIX]{x1D6FE})$
. De même, en remplaçant
${\mathcal{R}}_{\operatorname{cusp}}(\unicode[STIX]{x1D6FE})$
. De même, en remplaçant
![]() $n$
par
$n$
par
![]() $n_{j}$
pour
$n_{j}$
pour
![]() $j=1,2$
, à
$j=1,2$
, à
![]() $(\unicode[STIX]{x1D706}_{j},\unicode[STIX]{x1D716}_{j})$
sont associés des termes
$(\unicode[STIX]{x1D706}_{j},\unicode[STIX]{x1D716}_{j})$
sont associés des termes
![]() $\unicode[STIX]{x1D6FE}_{1}$
et
$\unicode[STIX]{x1D6FE}_{1}$
et
![]() $\unicode[STIX]{x1D6FE}_{2}$
analogues. Ainsi qu’on l’a remarqué ci-dessus, il faut considérer que
$\unicode[STIX]{x1D6FE}_{2}$
analogues. Ainsi qu’on l’a remarqué ci-dessus, il faut considérer que
![]() $(\unicode[STIX]{x1D706}_{j},\unicode[STIX]{x1D716}_{j})$
est le premier couple d’un quadruplet
$(\unicode[STIX]{x1D706}_{j},\unicode[STIX]{x1D716}_{j})$
est le premier couple d’un quadruplet
![]() $(\unicode[STIX]{x1D706}_{j}^{+},\unicode[STIX]{x1D716}_{j}^{+},\unicode[STIX]{x1D706}_{j}^{-},\unicode[STIX]{x1D716}_{j}^{-})$
dont le second couple est trivial. On voit que
$(\unicode[STIX]{x1D706}_{j}^{+},\unicode[STIX]{x1D716}_{j}^{+},\unicode[STIX]{x1D706}_{j}^{-},\unicode[STIX]{x1D716}_{j}^{-})$
dont le second couple est trivial. On voit que
![]() $\unicode[STIX]{x1D6FE}_{j}$
est de la forme
$\unicode[STIX]{x1D6FE}_{j}$
est de la forme
![]() $(r_{j}^{\prime },r_{j}^{\prime \prime },N_{j},0)$
. L’élément
$(r_{j}^{\prime },r_{j}^{\prime \prime },N_{j},0)$
. L’élément
![]() $\operatorname{proj}_{\operatorname{cusp}}(\boldsymbol{\unicode[STIX]{x1D70C}}_{\unicode[STIX]{x1D706}_{j},\unicode[STIX]{x1D716}_{j}})$
appartient à
$\operatorname{proj}_{\operatorname{cusp}}(\boldsymbol{\unicode[STIX]{x1D70C}}_{\unicode[STIX]{x1D706}_{j},\unicode[STIX]{x1D716}_{j}})$
appartient à
![]() ${\mathcal{R}}_{\operatorname{cusp}}(\unicode[STIX]{x1D6FE}_{j})$
. En considérant la recette de [Reference Waldspurger11] 1.11 qui calcule
${\mathcal{R}}_{\operatorname{cusp}}(\unicode[STIX]{x1D6FE}_{j})$
. En considérant la recette de [Reference Waldspurger11] 1.11 qui calcule
![]() $r^{\prime },r^{\prime \prime },r_{1}^{\prime },r_{1}^{\prime \prime },r_{2}^{\prime },r_{2}^{\prime \prime }$
en fonction de
$r^{\prime },r^{\prime \prime },r_{1}^{\prime },r_{1}^{\prime \prime },r_{2}^{\prime },r_{2}^{\prime \prime }$
en fonction de
![]() $k_{1}$
et
$k_{1}$
et
![]() $k_{2}$
, on constate que
$k_{2}$
, on constate que
![]() $r_{1}^{\prime },r_{1}^{\prime \prime },r_{2}^{\prime },r_{2}^{\prime \prime }$
se déduisent de
$r_{1}^{\prime },r_{1}^{\prime \prime },r_{2}^{\prime },r_{2}^{\prime \prime }$
se déduisent de
![]() $(r^{\prime },r^{\prime \prime })$
par les formules de 1.2. On est alors dans la situation de ce paragraphe, les fonctions
$(r^{\prime },r^{\prime \prime })$
par les formules de 1.2. On est alors dans la situation de ce paragraphe, les fonctions
![]() $\unicode[STIX]{x1D711}^{\prime }$
et
$\unicode[STIX]{x1D711}^{\prime }$
et
![]() $\unicode[STIX]{x1D711}^{\prime \prime }$
étant respectivement
$\unicode[STIX]{x1D711}^{\prime \prime }$
étant respectivement
![]() $\operatorname{proj}_{\operatorname{cusp}}(\boldsymbol{\unicode[STIX]{x1D70C}}_{\unicode[STIX]{x1D706}_{1},\unicode[STIX]{x1D716}_{1}})$
et
$\operatorname{proj}_{\operatorname{cusp}}(\boldsymbol{\unicode[STIX]{x1D70C}}_{\unicode[STIX]{x1D706}_{1},\unicode[STIX]{x1D716}_{1}})$
et
![]() $\operatorname{proj}_{\operatorname{cusp}}(\boldsymbol{\unicode[STIX]{x1D70C}}_{\unicode[STIX]{x1D706}_{2},\unicode[STIX]{x1D716}_{2}})$
. La proposition 1.2 affirme que les propriétés (5)(a) et (5)(b) sont vérifiées. Cela achève la démonstration.◻
$\operatorname{proj}_{\operatorname{cusp}}(\boldsymbol{\unicode[STIX]{x1D70C}}_{\unicode[STIX]{x1D706}_{2},\unicode[STIX]{x1D716}_{2}})$
. La proposition 1.2 affirme que les propriétés (5)(a) et (5)(b) sont vérifiées. Cela achève la démonstration.◻
1.4 Démonstration du théorème 2.1 de [Reference Waldspurger11]
Soit
![]() $h\in \operatorname{Sp}(2n;\mathbb{C})$
tel que
$h\in \operatorname{Sp}(2n;\mathbb{C})$
tel que
![]() $h^{2}=1$
, auquel est associé un couple
$h^{2}=1$
, auquel est associé un couple
![]() $(n_{1},n_{2})\in D(n)$
. Pour
$(n_{1},n_{2})\in D(n)$
. Pour
![]() $j=1,2$
, soit
$j=1,2$
, soit
![]() $(\unicode[STIX]{x1D706}_{j},s_{j},1)\in \mathfrak{St}_{n_{j},\operatorname{tunip}}$
. Pour
$(\unicode[STIX]{x1D706}_{j},s_{j},1)\in \mathfrak{St}_{n_{j},\operatorname{tunip}}$
. Pour
![]() $j=1,2$
, notons
$j=1,2$
, notons
![]() $\cup _{b\in B_{j}}\{s_{j,b},s_{j,b}^{-1}\}$
l’ensemble des valeurs propres de
$\cup _{b\in B_{j}}\{s_{j,b},s_{j,b}^{-1}\}$
l’ensemble des valeurs propres de
![]() $s_{j}$
autres que
$s_{j}$
autres que
![]() $\pm 1$
et notons
$\pm 1$
et notons
la décomposition de
![]() $\unicode[STIX]{x1D706}_{j}$
associée à
$\unicode[STIX]{x1D706}_{j}$
associée à
![]() $s_{j}$
, cf. [Reference Waldspurger11] 2.1. Posons
$s_{j}$
, cf. [Reference Waldspurger11] 2.1. Posons
![]() $\unicode[STIX]{x1D706}_{j,0}=\unicode[STIX]{x1D706}_{j}^{+}\cup \unicode[STIX]{x1D706}_{j}^{-}$
,
$\unicode[STIX]{x1D706}_{j,0}=\unicode[STIX]{x1D706}_{j}^{+}\cup \unicode[STIX]{x1D706}_{j}^{-}$
,
![]() $n_{j,0}=S(\unicode[STIX]{x1D706}_{j,0})/2$
et
$n_{j,0}=S(\unicode[STIX]{x1D706}_{j,0})/2$
et
![]() $m_{j,b}=S(\unicode[STIX]{x1D706}_{j,b})$
pour
$m_{j,b}=S(\unicode[STIX]{x1D706}_{j,b})$
pour
![]() $b\in B_{j}$
. Introduisons un sous-groupe parabolique
$b\in B_{j}$
. Introduisons un sous-groupe parabolique
![]() $P_{j}$
de
$P_{j}$
de
![]() $G_{n_{j},\operatorname{iso}}$
de composante de Levi
$G_{n_{j},\operatorname{iso}}$
de composante de Levi
Pour tout
![]() $b\in B_{j}$
, soit
$b\in B_{j}$
, soit
![]() $\unicode[STIX]{x1D712}_{j,b}$
le caractère non ramifié de
$\unicode[STIX]{x1D712}_{j,b}$
le caractère non ramifié de
![]() $F^{\times }$
tel que
$F^{\times }$
tel que
![]() $\unicode[STIX]{x1D712}_{j,b}(\unicode[STIX]{x1D71B})=s_{j,b}$
. L’élément
$\unicode[STIX]{x1D712}_{j,b}(\unicode[STIX]{x1D71B})=s_{j,b}$
. L’élément
![]() $s_{j}$
se restreint en un élément
$s_{j}$
se restreint en un élément
![]() $s_{j,0}\in \operatorname{Sp}(2n_{j,0};\mathbb{C})$
de sorte que
$s_{j,0}\in \operatorname{Sp}(2n_{j,0};\mathbb{C})$
de sorte que
![]() $\unicode[STIX]{x1D706}_{j,0}=\unicode[STIX]{x1D706}_{j}^{+}\cup \unicode[STIX]{x1D706}_{j}^{-}$
soit la décomposition de
$\unicode[STIX]{x1D706}_{j,0}=\unicode[STIX]{x1D706}_{j}^{+}\cup \unicode[STIX]{x1D706}_{j}^{-}$
soit la décomposition de
![]() $\unicode[STIX]{x1D706}_{j,0}$
associée à cet élément. Introduisons la représentation de
$\unicode[STIX]{x1D706}_{j,0}$
associée à cet élément. Introduisons la représentation de
![]() $M_{j}(F)$
$M_{j}(F)$
(on rappelle que
![]() $st_{m}$
est la représentation de Steinberg de
$st_{m}$
est la représentation de Steinberg de
![]() $\operatorname{GL}(m;F)$
). Il est connu que
$\operatorname{GL}(m;F)$
). Il est connu que
Introduisons le triplet
![]() $(\unicode[STIX]{x1D706},s,h)$
associé à
$(\unicode[STIX]{x1D706},s,h)$
associé à
![]() $h$
,
$h$
,
![]() $(\unicode[STIX]{x1D706}_{1},s_{1},1)$
et
$(\unicode[STIX]{x1D706}_{1},s_{1},1)$
et
![]() $(\unicode[STIX]{x1D706}_{2},s_{2},1)$
. Posons
$(\unicode[STIX]{x1D706}_{2},s_{2},1)$
. Posons
![]() $n_{0}=n_{0,1}+n_{0,2}$
. Soit
$n_{0}=n_{0,1}+n_{0,2}$
. Soit
![]() $\sharp =\operatorname{iso}$
ou
$\sharp =\operatorname{iso}$
ou
![]() $\operatorname{an}$
. Dans le cas
$\operatorname{an}$
. Dans le cas
![]() $\sharp =an$
, supposons provisoirement que
$\sharp =an$
, supposons provisoirement que
![]() $n_{0}\geqslant 1$
. On introduit un sous-groupe parabolique
$n_{0}\geqslant 1$
. On introduit un sous-groupe parabolique
![]() $P$
de
$P$
de
![]() $G_{\sharp }$
de composante de Levi
$G_{\sharp }$
de composante de Levi
Parce que l’élément
![]() $h$
commute à
$h$
commute à
![]() $s$
, il se restreint en un élément
$s$
, il se restreint en un élément
![]() $h_{0}\in \operatorname{Sp}(2n_{0};\mathbb{C})$
et la représentation
$h_{0}\in \operatorname{Sp}(2n_{0};\mathbb{C})$
et la représentation
![]() $\unicode[STIX]{x1D6F1}_{\sharp }(\unicode[STIX]{x1D706}_{0},s_{0},h_{0})$
de
$\unicode[STIX]{x1D6F1}_{\sharp }(\unicode[STIX]{x1D706}_{0},s_{0},h_{0})$
de
![]() $G_{n_{0},\sharp }(F)$
est bien définie. On introduit la représentation de
$G_{n_{0},\sharp }(F)$
est bien définie. On introduit la représentation de
![]() $M(F)$
$M(F)$
On vérifie que
Pour
![]() $j=1,2$
, le triplet
$j=1,2$
, le triplet
![]() $(\unicode[STIX]{x1D706}_{j,0},s_{j,0},1)$
appartient à
$(\unicode[STIX]{x1D706}_{j,0},s_{j,0},1)$
appartient à
![]() $\mathfrak{St}_{n_{j,0},\operatorname{unip}\!{-}\text{quad}}$
. Le théorème 1.3 entraîne que
$\mathfrak{St}_{n_{j,0},\operatorname{unip}\!{-}\text{quad}}$
. Le théorème 1.3 entraîne que
Le transfert
![]() $\text{transfert}_{h_{0},\sharp }$
se prolonge en un transfert entre les groupes
$\text{transfert}_{h_{0},\sharp }$
se prolonge en un transfert entre les groupes
![]() $M_{1}\times M_{2}$
et
$M_{1}\times M_{2}$
et
![]() $M$
(le transfert étant l’identité sur les composantes
$M$
(le transfert étant l’identité sur les composantes
![]() $\operatorname{GL}(m_{j,b})$
). Pour celui-là,
$\operatorname{GL}(m_{j,b})$
). Pour celui-là,
![]() $\unicode[STIX]{x1D70E}_{1}\,\otimes \,\unicode[STIX]{x1D70E}_{2}$
se transfère en
$\unicode[STIX]{x1D70E}_{1}\,\otimes \,\unicode[STIX]{x1D70E}_{2}$
se transfère en
![]() $\operatorname{sgn}_{\sharp }\unicode[STIX]{x1D70E}$
. Mais on sait que le transfert commute à l’induction. Il résulte alors des descriptions ci-dessus que
$\operatorname{sgn}_{\sharp }\unicode[STIX]{x1D70E}$
. Mais on sait que le transfert commute à l’induction. Il résulte alors des descriptions ci-dessus que
Dans le cas particulier où
![]() $\sharp =an$
et
$\sharp =an$
et
![]() $n_{0}=0$
, il n’y a plus de sous-groupe parabolique
$n_{0}=0$
, il n’y a plus de sous-groupe parabolique
![]() $P$
. Le membre de droite ci-dessus est nul car c’est le transfert d’une induite à partir d’un sous-groupe parabolique qui n’est pas relevant pour
$P$
. Le membre de droite ci-dessus est nul car c’est le transfert d’une induite à partir d’un sous-groupe parabolique qui n’est pas relevant pour
![]() $G_{\sharp }$
. Le membre de gauche est nul lui aussi car, d’après la relation [Reference Waldspurger11] 1.3(1), toutes les composantes irréductibles de
$G_{\sharp }$
. Le membre de gauche est nul lui aussi car, d’après la relation [Reference Waldspurger11] 1.3(1), toutes les composantes irréductibles de
![]() $\unicode[STIX]{x1D6F1}(\unicode[STIX]{x1D706},s,h)$
vivent sur l’unique groupe
$\unicode[STIX]{x1D6F1}(\unicode[STIX]{x1D706},s,h)$
vivent sur l’unique groupe
![]() $G_{\operatorname{iso}}(F)$
. L’égalité ci-dessus est donc aussi vérifiée dans ce cas particulier. Elle démontre le théorème 2.1 de [Reference Waldspurger11].◻
$G_{\operatorname{iso}}(F)$
. L’égalité ci-dessus est donc aussi vérifiée dans ce cas particulier. Elle démontre le théorème 2.1 de [Reference Waldspurger11].◻
2 Trois lemmes de transfert pour des algèbres de Lie
2.1 Le cas spécial orthogonal impair
Cette section et la suivante s’appuient sur les calculs déjà faits dans [Reference Moeglin and Waldspurger6]. On n’a guère envie de reproduire ces calculs, ni les définitions compliquées des objets qui y apparaissent. On se contentera d’indiquer les références nécessaires. Dans cette section, on va énoncer des lemmes de transfert pour des algèbres de Lie. Il y a trois cas : le cas spécial orthogonal impair, le cas spécial orthogonal pair et le cas unitaire. Les preuves sont similaires dans les trois cas (et beaucoup plus faciles dans le dernier). On n’écrira que celle concernant le cas spécial orthogonal pair, qui est le plus subtil. Dans ces trois paragraphes, on oublie les objets
![]() $n$
,
$n$
,
![]() $G_{\operatorname{iso}}$
et
$G_{\operatorname{iso}}$
et
![]() $G_{\operatorname{an}}$
précédemment fixés afin de libérer ces notations. On va introduire de nouveaux entiers
$G_{\operatorname{an}}$
précédemment fixés afin de libérer ces notations. On va introduire de nouveaux entiers
![]() $n$
et on conserve l’hypothèse
$n$
et on conserve l’hypothèse
![]() $p>6n+4$
.
$p>6n+4$
.
Dans ce paragraphe, on considère un entier
![]() $n\geqslant 1$
et un élément
$n\geqslant 1$
et un élément
![]() $\unicode[STIX]{x1D702}\in F^{\times }/F^{\times 2}$
. On construit comme en [Reference Waldspurger11] 1.1 les deux espaces quadratiques
$\unicode[STIX]{x1D702}\in F^{\times }/F^{\times 2}$
. On construit comme en [Reference Waldspurger11] 1.1 les deux espaces quadratiques
![]() $(V_{\operatorname{iso}},Q_{\operatorname{iso}})$
et
$(V_{\operatorname{iso}},Q_{\operatorname{iso}})$
et
![]() $(V_{\operatorname{an}},Q_{\operatorname{an}})$
définis sur
$(V_{\operatorname{an}},Q_{\operatorname{an}})$
définis sur
![]() $F$
tels que
$F$
tels que
![]() $\operatorname{dim}_{F}(V_{\operatorname{iso}})=\operatorname{dim}_{F}(V_{\operatorname{an}})=2n+1$
et
$\operatorname{dim}_{F}(V_{\operatorname{iso}})=\operatorname{dim}_{F}(V_{\operatorname{an}})=2n+1$
et
![]() $\unicode[STIX]{x1D702}(Q_{\operatorname{iso}})=\unicode[STIX]{x1D702}(Q_{\operatorname{an}})=\unicode[STIX]{x1D702}$
. On note
$\unicode[STIX]{x1D702}(Q_{\operatorname{iso}})=\unicode[STIX]{x1D702}(Q_{\operatorname{an}})=\unicode[STIX]{x1D702}$
. On note
![]() $G_{\operatorname{iso}}$
et
$G_{\operatorname{iso}}$
et
![]() $G_{\operatorname{an}}$
leurs groupes spéciaux orthogonaux. On considère quatre entiers
$G_{\operatorname{an}}$
leurs groupes spéciaux orthogonaux. On considère quatre entiers
![]() $r^{\prime },r^{\prime \prime },N^{\prime },N^{\prime \prime }\in \mathbb{N}$
tels que
$r^{\prime },r^{\prime \prime },N^{\prime },N^{\prime \prime }\in \mathbb{N}$
tels que
On pose
![]() $N=N^{\prime }+N^{\prime \prime }$
. On a défini en [Reference Moeglin and Waldspurger6] 3.11 et 3.12 une application
$N=N^{\prime }+N^{\prime \prime }$
. On a défini en [Reference Moeglin and Waldspurger6] 3.11 et 3.12 une application
(en [Reference Moeglin and Waldspurger6], l’indice
![]() $\operatorname{cusp}$
était remplacé par
$\operatorname{cusp}$
était remplacé par
![]() $\text{ell}$
mais le sens était le même).
$\text{ell}$
mais le sens était le même).
Rappelons que, pour
![]() $m\in \mathbb{N}$
, les classes de conjugaison dans
$m\in \mathbb{N}$
, les classes de conjugaison dans
![]() $W_{m}$
sont paramétrées par les paires de partitions
$W_{m}$
sont paramétrées par les paires de partitions
![]() $(\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD})$
telles que
$(\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD})$
telles que
![]() $S(\unicode[STIX]{x1D6FC})+S(\unicode[STIX]{x1D6FD})=m$
. Pour
$S(\unicode[STIX]{x1D6FC})+S(\unicode[STIX]{x1D6FD})=m$
. Pour
![]() $w\in W_{m}$
, notons
$w\in W_{m}$
, notons
![]() $\unicode[STIX]{x1D711}_{w}$
la fonction caractéristique de la classe de conjugaison de
$\unicode[STIX]{x1D711}_{w}$
la fonction caractéristique de la classe de conjugaison de
![]() $w$
. Alors
$w$
. Alors
![]() $\mathbb{C}[{\hat{W}}_{m}]_{\operatorname{cusp}}$
a pour base les
$\mathbb{C}[{\hat{W}}_{m}]_{\operatorname{cusp}}$
a pour base les
![]() $\unicode[STIX]{x1D711}_{w}$
quand
$\unicode[STIX]{x1D711}_{w}$
quand
![]() $w$
décrit, à conjugaison près, les éléments dont la classe est paramétrée par un couple de partitions de la forme
$w$
décrit, à conjugaison près, les éléments dont la classe est paramétrée par un couple de partitions de la forme
![]() $(\emptyset ,\unicode[STIX]{x1D6FD})$
. On fixe des éléments
$(\emptyset ,\unicode[STIX]{x1D6FD})$
. On fixe des éléments
![]() $w^{\prime }\in W_{N^{\prime }}$
et
$w^{\prime }\in W_{N^{\prime }}$
et
![]() $w^{\prime \prime }\in W_{N^{\prime \prime }}$
dont les classes sont paramétrées par des couples de cette forme. On pose
$w^{\prime \prime }\in W_{N^{\prime \prime }}$
dont les classes sont paramétrées par des couples de cette forme. On pose
Soit
![]() $(n_{1},n_{2})\in D(n)$
. À ce couple est associée une donnée endoscopique de
$(n_{1},n_{2})\in D(n)$
. À ce couple est associée une donnée endoscopique de
![]() $G_{\operatorname{iso}}$
et
$G_{\operatorname{iso}}$
et
![]() $G_{\operatorname{an}}$
. On utilise les mêmes définitions qu’en 1.2. Celles-là s’appliquent aux algèbres de Lie, c’est-à-dire qu’il y a un transfert de
$G_{\operatorname{an}}$
. On utilise les mêmes définitions qu’en 1.2. Celles-là s’appliquent aux algèbres de Lie, c’est-à-dire qu’il y a un transfert de
![]() $C_{\operatorname{cusp}}^{\infty }(\mathfrak{g}_{\operatorname{iso}}(F))\oplus C_{\operatorname{cusp}}^{\infty }(\mathfrak{g}_{\operatorname{an}}(F))$
dans
$C_{\operatorname{cusp}}^{\infty }(\mathfrak{g}_{\operatorname{iso}}(F))\oplus C_{\operatorname{cusp}}^{\infty }(\mathfrak{g}_{\operatorname{an}}(F))$
dans
On le note
![]() $\text{transfert}_{n_{1},n_{2}}$
. Le facteur de transfert est uniquement défini. Les formules en sont données en [Reference Waldspurger9] proposition X.8. Il convient de supprimer les discriminants de Weyl de ces formules, que l’on a incorporés aux intégrales orbitales. Le
$\text{transfert}_{n_{1},n_{2}}$
. Le facteur de transfert est uniquement défini. Les formules en sont données en [Reference Waldspurger9] proposition X.8. Il convient de supprimer les discriminants de Weyl de ces formules, que l’on a incorporés aux intégrales orbitales. Le
![]() $\unicode[STIX]{x1D702}$
de la définition X.7 de [Reference Waldspurger9] n’est pas notre présent
$\unicode[STIX]{x1D702}$
de la définition X.7 de [Reference Waldspurger9] n’est pas notre présent
![]() $\unicode[STIX]{x1D702}$
, c’est
$\unicode[STIX]{x1D702}$
, c’est
![]() $(-1)^{n}\unicode[STIX]{x1D702}$
.
$(-1)^{n}\unicode[STIX]{x1D702}$
.
Fixons
![]() $\unicode[STIX]{x1D702}_{1},\unicode[STIX]{x1D702}_{2}\in F^{\times }/F^{\times 2}$
tels que
$\unicode[STIX]{x1D702}_{1},\unicode[STIX]{x1D702}_{2}\in F^{\times }/F^{\times 2}$
tels que
![]() $\unicode[STIX]{x1D702}_{1}\unicode[STIX]{x1D702}_{2}=\unicode[STIX]{x1D702}$
. Notons
$\unicode[STIX]{x1D702}_{1}\unicode[STIX]{x1D702}_{2}=\unicode[STIX]{x1D702}$
. Notons
![]() $t_{1}^{\prime }$
l’élément de l’ensemble
$t_{1}^{\prime }$
l’élément de l’ensemble
![]() $\{\frac{r^{\prime }+r^{\prime \prime }+1}{2},\frac{r^{\prime }+r^{\prime \prime }-1}{2}\}$
qui est de la même parité que
$\{\frac{r^{\prime }+r^{\prime \prime }+1}{2},\frac{r^{\prime }+r^{\prime \prime }-1}{2}\}$
qui est de la même parité que
![]() $1+\operatorname{val}_{F}(\unicode[STIX]{x1D702}_{1})$
. Notons
$1+\operatorname{val}_{F}(\unicode[STIX]{x1D702}_{1})$
. Notons
![]() $t_{1}^{\prime \prime }$
l’autre élément. Notons
$t_{1}^{\prime \prime }$
l’autre élément. Notons
![]() $t_{2}^{\prime }$
l’élément de l’ensemble
$t_{2}^{\prime }$
l’élément de l’ensemble
![]() $\{\frac{|r^{\prime }-r^{\prime \prime }|+1}{2},\frac{|r^{\prime }-r^{\prime \prime }|-1}{2}\}$
qui est de la même parité que
$\{\frac{|r^{\prime }-r^{\prime \prime }|+1}{2},\frac{|r^{\prime }-r^{\prime \prime }|-1}{2}\}$
qui est de la même parité que
![]() $1+\operatorname{val}_{F}(\unicode[STIX]{x1D702}_{2})$
. Notons
$1+\operatorname{val}_{F}(\unicode[STIX]{x1D702}_{2})$
. Notons
![]() $t_{2}^{\prime \prime }$
l’autre élément. Définissons deux entiers
$t_{2}^{\prime \prime }$
l’autre élément. Définissons deux entiers
![]() $n_{1}$
et
$n_{1}$
et
![]() $n_{2}$
par les formules
$n_{2}$
par les formules
qui sont équivalentes à
On vérifie que
![]() $n_{1}+n_{2}=n$
. Pour
$n_{1}+n_{2}=n$
. Pour
![]() $j=1,2$
, on peut considérer
$j=1,2$
, on peut considérer
![]() $G_{n_{j},\operatorname{iso}}$
et
$G_{n_{j},\operatorname{iso}}$
et
![]() $G_{n_{j},\operatorname{an}}$
comme les groupes spéciaux orthogonaux d’espaces quadratiques de discriminants
$G_{n_{j},\operatorname{an}}$
comme les groupes spéciaux orthogonaux d’espaces quadratiques de discriminants
![]() $\unicode[STIX]{x1D702}_{j}$
. On peut donc appliquer la même construction que ci-dessus, où le couple
$\unicode[STIX]{x1D702}_{j}$
. On peut donc appliquer la même construction que ci-dessus, où le couple
![]() $(N^{\prime },N^{\prime \prime })$
est remplacé par
$(N^{\prime },N^{\prime \prime })$
est remplacé par
![]() $(N^{\prime },0)$
si
$(N^{\prime },0)$
si
![]() $j=1$
ou par
$j=1$
ou par
![]() $(N^{\prime \prime },0)$
si
$(N^{\prime \prime },0)$
si
![]() $j=2$
. Cela nous permet de définir les éléments
$j=2$
. Cela nous permet de définir les éléments
Notons
![]() $\operatorname{sgn}$
l’unique caractère non trivial de
$\operatorname{sgn}$
l’unique caractère non trivial de
![]() $\mathfrak{o}^{\times }/\mathfrak{o}^{\times 2}$
. Définissons une constante
$\mathfrak{o}^{\times }/\mathfrak{o}^{\times 2}$
. Définissons une constante
![]() $C$
par les formules suivantes :
$C$
par les formules suivantes :
si
![]() $r^{\prime \prime }\leqslant r^{\prime }$
,
$r^{\prime \prime }\leqslant r^{\prime }$
,
![]() $C=\operatorname{sgn}(-1)^{\frac{r^{\prime }+r^{\prime \prime }-1}{2}}\operatorname{sgn}(-\unicode[STIX]{x1D702}_{2}\unicode[STIX]{x1D71B}^{-\operatorname{val}_{F}(\unicode[STIX]{x1D702}_{2})})^{\operatorname{val}_{F}(\unicode[STIX]{x1D702})}$
;
$C=\operatorname{sgn}(-1)^{\frac{r^{\prime }+r^{\prime \prime }-1}{2}}\operatorname{sgn}(-\unicode[STIX]{x1D702}_{2}\unicode[STIX]{x1D71B}^{-\operatorname{val}_{F}(\unicode[STIX]{x1D702}_{2})})^{\operatorname{val}_{F}(\unicode[STIX]{x1D702})}$
;
si
![]() $r^{\prime }<r^{\prime \prime }$
,
$r^{\prime }<r^{\prime \prime }$
,
![]() $C=\operatorname{sgn}(-1)^{\frac{r^{\prime }+r^{\prime \prime }-1}{2}}\operatorname{sgn}_{CD}(w^{\prime \prime })\operatorname{sgn}(-\unicode[STIX]{x1D702}_{2}\unicode[STIX]{x1D71B}^{-\operatorname{val}_{F}(\unicode[STIX]{x1D702}_{2})})^{1+\operatorname{val}_{F}(\unicode[STIX]{x1D702})}$
.
$C=\operatorname{sgn}(-1)^{\frac{r^{\prime }+r^{\prime \prime }-1}{2}}\operatorname{sgn}_{CD}(w^{\prime \prime })\operatorname{sgn}(-\unicode[STIX]{x1D702}_{2}\unicode[STIX]{x1D71B}^{-\operatorname{val}_{F}(\unicode[STIX]{x1D702}_{2})})^{1+\operatorname{val}_{F}(\unicode[STIX]{x1D702})}$
.
Lemme.
(i) On a l’égalité
 $\text{transfert}_{n_{1},n_{2}}(f)=Cf_{1}\,\otimes \,f_{2}$
.
$\text{transfert}_{n_{1},n_{2}}(f)=Cf_{1}\,\otimes \,f_{2}$
.(ii) Soit
 $(\bar{n}_{1},\bar{n}_{2})\in D(n)$
un couple différent de
$(\bar{n}_{1},\bar{n}_{2})\in D(n)$
un couple différent de
 $(n_{1},n_{2})$
. Alors
$(n_{1},n_{2})$
. Alors
 $\text{transfert}_{\bar{n}_{1},\bar{n}_{2}}(f)=0$
.
$\text{transfert}_{\bar{n}_{1},\bar{n}_{2}}(f)=0$
.
2.2 Le cas spécial orthogonal pair
Dans ce paragraphe, on considère un entier
![]() $n\geqslant 1$
et un élément
$n\geqslant 1$
et un élément
![]() $\unicode[STIX]{x1D702}\in F^{\times }/F^{\times 2}$
. On exclut le cas
$\unicode[STIX]{x1D702}\in F^{\times }/F^{\times 2}$
. On exclut le cas
![]() $n=1$
,
$n=1$
,
![]() $\unicode[STIX]{x1D702}=1$
. On construit comme en [Reference Waldspurger11] 1.1 les deux espaces quadratiques
$\unicode[STIX]{x1D702}=1$
. On construit comme en [Reference Waldspurger11] 1.1 les deux espaces quadratiques
![]() $(V_{\operatorname{iso}},Q_{\operatorname{iso}})$
et
$(V_{\operatorname{iso}},Q_{\operatorname{iso}})$
et
![]() $(V_{\operatorname{an}},Q_{\operatorname{an}})$
définis sur
$(V_{\operatorname{an}},Q_{\operatorname{an}})$
définis sur
![]() $F$
tels que
$F$
tels que
![]() $\operatorname{dim}_{F}(V_{\operatorname{iso}})=\operatorname{dim}_{F}(V_{\operatorname{an}})=2n$
et
$\operatorname{dim}_{F}(V_{\operatorname{iso}})=\operatorname{dim}_{F}(V_{\operatorname{an}})=2n$
et
![]() $\unicode[STIX]{x1D702}(Q_{\operatorname{iso}})=\unicode[STIX]{x1D702}(Q_{\operatorname{an}})=\unicode[STIX]{x1D702}$
. On note
$\unicode[STIX]{x1D702}(Q_{\operatorname{iso}})=\unicode[STIX]{x1D702}(Q_{\operatorname{an}})=\unicode[STIX]{x1D702}$
. On note
![]() $G_{\unicode[STIX]{x1D702},\operatorname{iso}}$
et
$G_{\unicode[STIX]{x1D702},\operatorname{iso}}$
et
![]() $G_{\unicode[STIX]{x1D702},\operatorname{an}}$
leurs groupes spéciaux orthogonaux. On considère quatre entiers
$G_{\unicode[STIX]{x1D702},\operatorname{an}}$
leurs groupes spéciaux orthogonaux. On considère quatre entiers
![]() $r^{\prime },r^{\prime \prime },N^{\prime },N^{\prime \prime }\in \mathbb{N}$
tels que
$r^{\prime },r^{\prime \prime },N^{\prime },N^{\prime \prime }\in \mathbb{N}$
tels que
On pose
![]() $N=N^{\prime }+N^{\prime \prime }$
. On a défini en [Reference Moeglin and Waldspurger6] 3.11 et 3.12 une application
$N=N^{\prime }+N^{\prime \prime }$
. On a défini en [Reference Moeglin and Waldspurger6] 3.11 et 3.12 une application
On fixe des éléments
![]() $w^{\prime }\in W_{N^{\prime }}$
et
$w^{\prime }\in W_{N^{\prime }}$
et
![]() $w^{\prime \prime }\in W_{N^{\prime \prime }}$
dont les classes de conjugaison sont paramétrées par des couples de partitions de la forme
$w^{\prime \prime }\in W_{N^{\prime \prime }}$
dont les classes de conjugaison sont paramétrées par des couples de partitions de la forme
![]() $(\emptyset ,\unicode[STIX]{x1D6FD}^{\prime })$
et
$(\emptyset ,\unicode[STIX]{x1D6FD}^{\prime })$
et
![]() $(\emptyset ,\unicode[STIX]{x1D6FD}^{\prime \prime })$
. On pose
$(\emptyset ,\unicode[STIX]{x1D6FD}^{\prime \prime })$
. On pose
Remarque.
Dans le cas où
![]() $r^{\prime }=r^{\prime \prime }=0$
, cette fonction est nulle si le couple
$r^{\prime }=r^{\prime \prime }=0$
, cette fonction est nulle si le couple
![]() $(w^{\prime },w^{\prime \prime })$
ne vérifie pas la relation
$(w^{\prime },w^{\prime \prime })$
ne vérifie pas la relation
![]() $\operatorname{sgn}(\unicode[STIX]{x1D702}\unicode[STIX]{x1D71B}^{-\operatorname{val}_{F}(\unicode[STIX]{x1D702})})\operatorname{sgn}_{CD}(w^{\prime })\operatorname{sgn}_{CD}(w^{\prime \prime })=1$
.
$\operatorname{sgn}(\unicode[STIX]{x1D702}\unicode[STIX]{x1D71B}^{-\operatorname{val}_{F}(\unicode[STIX]{x1D702})})\operatorname{sgn}_{CD}(w^{\prime })\operatorname{sgn}_{CD}(w^{\prime \prime })=1$
.
Soit
![]() $(n_{1},n_{2})\in D(n)$
et soit
$(n_{1},n_{2})\in D(n)$
et soit
![]() $\unicode[STIX]{x1D702}_{1},\unicode[STIX]{x1D702}_{2}\in F^{\times }/F^{\times 2}$
tels que
$\unicode[STIX]{x1D702}_{1},\unicode[STIX]{x1D702}_{2}\in F^{\times }/F^{\times 2}$
tels que
![]() $\unicode[STIX]{x1D702}=\unicode[STIX]{x1D702}_{1}\unicode[STIX]{x1D702}_{2}$
. À ces objets est associée une donnée endoscopique de
$\unicode[STIX]{x1D702}=\unicode[STIX]{x1D702}_{1}\unicode[STIX]{x1D702}_{2}$
. À ces objets est associée une donnée endoscopique de
![]() $G_{\unicode[STIX]{x1D702},\operatorname{iso}}$
et
$G_{\unicode[STIX]{x1D702},\operatorname{iso}}$
et
![]() $G_{\unicode[STIX]{x1D702},\operatorname{an}}$
. Le groupe endoscopique de cette donnée est
$G_{\unicode[STIX]{x1D702},\operatorname{an}}$
. Le groupe endoscopique de cette donnée est
![]() $G_{n_{1},\unicode[STIX]{x1D702}_{1},\operatorname{iso}}\,\otimes \,G_{n_{2},\unicode[STIX]{x1D702}_{2},\operatorname{iso}}$
. De nouveau, il y a un transfert de
$G_{n_{1},\unicode[STIX]{x1D702}_{1},\operatorname{iso}}\,\otimes \,G_{n_{2},\unicode[STIX]{x1D702}_{2},\operatorname{iso}}$
. De nouveau, il y a un transfert de
![]() $C_{\operatorname{cusp}}^{\infty }(\mathfrak{g}_{\unicode[STIX]{x1D702},\operatorname{iso}}(F))\oplus C_{\operatorname{cusp}}^{\infty }(\mathfrak{g}_{\unicode[STIX]{x1D702},\operatorname{an}}(F))$
dans
$C_{\operatorname{cusp}}^{\infty }(\mathfrak{g}_{\unicode[STIX]{x1D702},\operatorname{iso}}(F))\oplus C_{\operatorname{cusp}}^{\infty }(\mathfrak{g}_{\unicode[STIX]{x1D702},\operatorname{an}}(F))$
dans
On le note
![]() $\text{transfert}_{n_{1},\unicode[STIX]{x1D702}_{1},n_{2},\unicode[STIX]{x1D702}_{2}}$
. Il y a un choix naturel de facteur de transfert. Les formules en sont données en [Reference Waldspurger9] proposition X.8. Il convient encore d’en supprimer les discriminants de Weyl. Le
$\text{transfert}_{n_{1},\unicode[STIX]{x1D702}_{1},n_{2},\unicode[STIX]{x1D702}_{2}}$
. Il y a un choix naturel de facteur de transfert. Les formules en sont données en [Reference Waldspurger9] proposition X.8. Il convient encore d’en supprimer les discriminants de Weyl. Le
![]() $\unicode[STIX]{x1D702}$
de la définition X.7 de [Reference Waldspurger9] n’est pas notre présent
$\unicode[STIX]{x1D702}$
de la définition X.7 de [Reference Waldspurger9] n’est pas notre présent
![]() $\unicode[STIX]{x1D702}$
, c’est
$\unicode[STIX]{x1D702}$
, c’est
![]() $(-1)^{n}\unicode[STIX]{x1D702}$
. On note
$(-1)^{n}\unicode[STIX]{x1D702}$
. On note
![]() $\unicode[STIX]{x1D6E5}_{n_{1},\unicode[STIX]{x1D702}_{1},n_{2},\unicode[STIX]{x1D702}_{2}}$
ce facteur de transfert.
$\unicode[STIX]{x1D6E5}_{n_{1},\unicode[STIX]{x1D702}_{1},n_{2},\unicode[STIX]{x1D702}_{2}}$
ce facteur de transfert.
Posons
Définissons deux entiers
![]() $n_{1}$
et
$n_{1}$
et
![]() $n_{2}$
par les formules
$n_{2}$
par les formules
qui sont équivalentes à
On vérifie que
![]() $n_{1}+n_{2}=n$
. Fixons
$n_{1}+n_{2}=n$
. Fixons
![]() $\unicode[STIX]{x1D702}_{1},\unicode[STIX]{x1D702}_{2}\in F^{\times }/F^{\times 2}$
tels que
$\unicode[STIX]{x1D702}_{1},\unicode[STIX]{x1D702}_{2}\in F^{\times }/F^{\times 2}$
tels que
![]() $\unicode[STIX]{x1D702}_{1}\unicode[STIX]{x1D702}_{2}=\unicode[STIX]{x1D702}$
et
$\unicode[STIX]{x1D702}_{1}\unicode[STIX]{x1D702}_{2}=\unicode[STIX]{x1D702}$
et
Pour
![]() $j=1,2$
, on peut appliquer la même construction que ci-dessus à
$j=1,2$
, on peut appliquer la même construction que ci-dessus à
![]() $n_{j}$
et
$n_{j}$
et
![]() $\unicode[STIX]{x1D702}_{j}$
, où le couple
$\unicode[STIX]{x1D702}_{j}$
, où le couple
![]() $(N^{\prime },N^{\prime \prime })$
est remplacé par
$(N^{\prime },N^{\prime \prime })$
est remplacé par
![]() $(N^{\prime },0)$
si
$(N^{\prime },0)$
si
![]() $j=1$
ou par
$j=1$
ou par
![]() $(N^{\prime \prime },0)$
si
$(N^{\prime \prime },0)$
si
![]() $j=2$
. Cela nous permet de définir les éléments
$j=2$
. Cela nous permet de définir les éléments
 $$\begin{eqnarray}\displaystyle f_{1,\unicode[STIX]{x1D702}_{1}} & = & \displaystyle {\mathcal{Q}}(t_{1}^{\prime },t_{1}^{\prime \prime })^{\operatorname{Lie}}\circ \unicode[STIX]{x1D70C}_{N^{\prime }}^{\ast }\circ \unicode[STIX]{x1D704}_{N^{\prime },0}(\unicode[STIX]{x1D711}_{w^{\prime }})\nonumber\\ \displaystyle & \in & \displaystyle C_{\operatorname{cusp}}^{\infty }(\mathfrak{g}_{n_{1},\unicode[STIX]{x1D702}_{1},\operatorname{iso}}(F))\oplus C_{\operatorname{cusp}}^{\infty }(\mathfrak{g}_{n_{1},\unicode[STIX]{x1D702}_{1},\operatorname{an}}(F)),\nonumber\\ \displaystyle f_{2,\unicode[STIX]{x1D702}_{2}} & = & \displaystyle {\mathcal{Q}}(t_{2}^{\prime },t_{2}^{\prime \prime })^{\operatorname{Lie}}\circ \unicode[STIX]{x1D70C}_{N^{\prime \prime }}^{\ast }\circ \unicode[STIX]{x1D704}_{N^{\prime \prime },0}(\unicode[STIX]{x1D711}_{w^{\prime \prime }})\nonumber\\ \displaystyle & \in & \displaystyle C_{\operatorname{cusp}}^{\infty }(\mathfrak{g}_{n_{2},\unicode[STIX]{x1D702}_{2},\operatorname{iso}}(F))\oplus C_{\operatorname{cusp}}^{\infty }(\mathfrak{g}_{n_{2},\unicode[STIX]{x1D702}_{2},\operatorname{an}}(F)).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle f_{1,\unicode[STIX]{x1D702}_{1}} & = & \displaystyle {\mathcal{Q}}(t_{1}^{\prime },t_{1}^{\prime \prime })^{\operatorname{Lie}}\circ \unicode[STIX]{x1D70C}_{N^{\prime }}^{\ast }\circ \unicode[STIX]{x1D704}_{N^{\prime },0}(\unicode[STIX]{x1D711}_{w^{\prime }})\nonumber\\ \displaystyle & \in & \displaystyle C_{\operatorname{cusp}}^{\infty }(\mathfrak{g}_{n_{1},\unicode[STIX]{x1D702}_{1},\operatorname{iso}}(F))\oplus C_{\operatorname{cusp}}^{\infty }(\mathfrak{g}_{n_{1},\unicode[STIX]{x1D702}_{1},\operatorname{an}}(F)),\nonumber\\ \displaystyle f_{2,\unicode[STIX]{x1D702}_{2}} & = & \displaystyle {\mathcal{Q}}(t_{2}^{\prime },t_{2}^{\prime \prime })^{\operatorname{Lie}}\circ \unicode[STIX]{x1D70C}_{N^{\prime \prime }}^{\ast }\circ \unicode[STIX]{x1D704}_{N^{\prime \prime },0}(\unicode[STIX]{x1D711}_{w^{\prime \prime }})\nonumber\\ \displaystyle & \in & \displaystyle C_{\operatorname{cusp}}^{\infty }(\mathfrak{g}_{n_{2},\unicode[STIX]{x1D702}_{2},\operatorname{iso}}(F))\oplus C_{\operatorname{cusp}}^{\infty }(\mathfrak{g}_{n_{2},\unicode[STIX]{x1D702}_{2},\operatorname{an}}(F)).\nonumber\end{eqnarray}$$
Définissons une constante
![]() $C_{\unicode[STIX]{x1D702}_{1},\unicode[STIX]{x1D702}_{2}}$
par les formules suivantes :
$C_{\unicode[STIX]{x1D702}_{1},\unicode[STIX]{x1D702}_{2}}$
par les formules suivantes :
si
![]() $r^{\prime \prime }\leqslant r^{\prime }$
,
$r^{\prime \prime }\leqslant r^{\prime }$
,
![]() $C_{\unicode[STIX]{x1D702}_{1},\unicode[STIX]{x1D702}_{2}}=\operatorname{sgn}(\unicode[STIX]{x1D702}_{2}\unicode[STIX]{x1D71B}^{-\operatorname{val}_{F}(\unicode[STIX]{x1D702}_{2})})^{\operatorname{val}_{F}(\unicode[STIX]{x1D702})}$
;
$C_{\unicode[STIX]{x1D702}_{1},\unicode[STIX]{x1D702}_{2}}=\operatorname{sgn}(\unicode[STIX]{x1D702}_{2}\unicode[STIX]{x1D71B}^{-\operatorname{val}_{F}(\unicode[STIX]{x1D702}_{2})})^{\operatorname{val}_{F}(\unicode[STIX]{x1D702})}$
;
si
![]() $r^{\prime }<r^{\prime \prime }$
,
$r^{\prime }<r^{\prime \prime }$
,
![]() $C_{\unicode[STIX]{x1D702}_{1},\unicode[STIX]{x1D702}_{2}}=\operatorname{sgn}(-1)^{\operatorname{val}_{F}(\unicode[STIX]{x1D702}_{2})}\operatorname{sgn}_{CD}(w^{\prime \prime })\operatorname{sgn}(\unicode[STIX]{x1D702}_{2}\unicode[STIX]{x1D71B}^{-\operatorname{val}_{F}(\unicode[STIX]{x1D702}_{2})})^{1+\operatorname{val}_{F}(\unicode[STIX]{x1D702})}$
.
$C_{\unicode[STIX]{x1D702}_{1},\unicode[STIX]{x1D702}_{2}}=\operatorname{sgn}(-1)^{\operatorname{val}_{F}(\unicode[STIX]{x1D702}_{2})}\operatorname{sgn}_{CD}(w^{\prime \prime })\operatorname{sgn}(\unicode[STIX]{x1D702}_{2}\unicode[STIX]{x1D71B}^{-\operatorname{val}_{F}(\unicode[STIX]{x1D702}_{2})})^{1+\operatorname{val}_{F}(\unicode[STIX]{x1D702})}$
.
Lemme. Soit
![]() $\unicode[STIX]{x1D702}_{1},\unicode[STIX]{x1D702}_{2}\in F^{\times }/F^{\times 2}$
tels que
$\unicode[STIX]{x1D702}_{1},\unicode[STIX]{x1D702}_{2}\in F^{\times }/F^{\times 2}$
tels que
![]() $\unicode[STIX]{x1D702}_{1}\unicode[STIX]{x1D702}_{2}=\unicode[STIX]{x1D702}$
.
$\unicode[STIX]{x1D702}_{1}\unicode[STIX]{x1D702}_{2}=\unicode[STIX]{x1D702}$
.
(i) Si (1) est vérifié, on a l’égalité
 $\text{transfert}_{n_{1},\unicode[STIX]{x1D702}_{1},n_{2},\unicode[STIX]{x1D702}_{2}}(f)=C_{\unicode[STIX]{x1D702}_{1},\unicode[STIX]{x1D702}_{2}}f_{1,\unicode[STIX]{x1D702}_{1}}\,\otimes \,f_{2,\unicode[STIX]{x1D702}_{2}}$
.
$\text{transfert}_{n_{1},\unicode[STIX]{x1D702}_{1},n_{2},\unicode[STIX]{x1D702}_{2}}(f)=C_{\unicode[STIX]{x1D702}_{1},\unicode[STIX]{x1D702}_{2}}f_{1,\unicode[STIX]{x1D702}_{1}}\,\otimes \,f_{2,\unicode[STIX]{x1D702}_{2}}$
.(ii) Soit
 $(\bar{n}_{1},\bar{n}_{2})\in D(n)$
. Supposons que
$(\bar{n}_{1},\bar{n}_{2})\in D(n)$
. Supposons que
 $(\bar{n}_{1},\bar{n}_{2})\not =(n_{1},n_{2})$
ou que (1) ne soit pas vérifié. Alors
$(\bar{n}_{1},\bar{n}_{2})\not =(n_{1},n_{2})$
ou que (1) ne soit pas vérifié. Alors
 $\text{transfert}_{\bar{n}_{1},\unicode[STIX]{x1D702}_{1},\bar{n}_{2},\unicode[STIX]{x1D702}_{2}}(f)=0$
.
$\text{transfert}_{\bar{n}_{1},\unicode[STIX]{x1D702}_{1},\bar{n}_{2},\unicode[STIX]{x1D702}_{2}}(f)=0$
.
La démonstration de ce lemme occupe les paragraphes 2.4 à 2.8.
2.3 Le cas unitaire
Dans ce paragraphe, on fixe une tour d’extensions finies non ramifiées
![]() $E/E^{\natural }/F$
, avec
$E/E^{\natural }/F$
, avec
![]() $[E:E^{\natural }]=2$
, et un entier
$[E:E^{\natural }]=2$
, et un entier
![]() $d\geqslant 1$
. On considère les espaces vectoriels
$d\geqslant 1$
. On considère les espaces vectoriels
![]() $V$
sur
$V$
sur
![]() $E$
, de dimension
$E$
, de dimension
![]() $d$
, munis d’une forme hermitienne non dégénérée
$d$
, munis d’une forme hermitienne non dégénérée
![]() $Q$
, relativement à l’extension
$Q$
, relativement à l’extension
![]() $E/E^{\natural }$
. De nouveau, il y a deux classes d’isomorphie de couples
$E/E^{\natural }$
. De nouveau, il y a deux classes d’isomorphie de couples
![]() $(V,Q)$
, qui se distinguent par la valuation du déterminant de
$(V,Q)$
, qui se distinguent par la valuation du déterminant de
![]() $Q$
(ce déterminant est un élément de
$Q$
(ce déterminant est un élément de
![]() $E^{\natural ,\times }/\operatorname{norme}_{E/E^{\natural }}(E^{\times })$
, sa valuation est l’image de ce terme dans
$E^{\natural ,\times }/\operatorname{norme}_{E/E^{\natural }}(E^{\times })$
, sa valuation est l’image de ce terme dans
![]() $\mathbb{Z}/2\mathbb{Z}$
par l’application
$\mathbb{Z}/2\mathbb{Z}$
par l’application
![]() $\operatorname{val}_{E^{\natural }}$
). On note
$\operatorname{val}_{E^{\natural }}$
). On note
![]() $(V_{\operatorname{iso}},Q_{\operatorname{iso}})$
celui pour lequel cette valuation est paire et
$(V_{\operatorname{iso}},Q_{\operatorname{iso}})$
celui pour lequel cette valuation est paire et
![]() $(V_{\operatorname{an}},Q_{\operatorname{an}})$
celui pour lequel cette valuation est impaire. On note
$(V_{\operatorname{an}},Q_{\operatorname{an}})$
celui pour lequel cette valuation est impaire. On note
![]() $G_{\operatorname{iso}}$
et
$G_{\operatorname{iso}}$
et
![]() $G_{\operatorname{an}}$
les groupes unitaires de ces espaces hermitiens.
$G_{\operatorname{an}}$
les groupes unitaires de ces espaces hermitiens.
Pour
![]() $m\in \mathbb{N}$
, on sait que les classes de conjugaison dans
$m\in \mathbb{N}$
, on sait que les classes de conjugaison dans
![]() $\mathfrak{S}_{m}$
sont paramétrées par les partitions de
$\mathfrak{S}_{m}$
sont paramétrées par les partitions de
![]() $m$
. On note
$m$
. On note
![]() $\mathbb{C}[\hat{\mathfrak{S}}_{m}]_{U-\operatorname{cusp}}$
l’espace des fonctions sur
$\mathbb{C}[\hat{\mathfrak{S}}_{m}]_{U-\operatorname{cusp}}$
l’espace des fonctions sur
![]() $\mathfrak{S}_{m}$
, invariantes par conjugaison, à support dans des classes de conjugaison paramétrées par des partitions dont tous les termes non nuls sont impairs.
$\mathfrak{S}_{m}$
, invariantes par conjugaison, à support dans des classes de conjugaison paramétrées par des partitions dont tous les termes non nuls sont impairs.
Soit
![]() $(d^{\prime },d^{\prime \prime })\in D(d)$
. Dans [Reference Moeglin and Waldspurger6] 3.1, 3.2, 3.3 et 3.12, on a défini une application
$(d^{\prime },d^{\prime \prime })\in D(d)$
. Dans [Reference Moeglin and Waldspurger6] 3.1, 3.2, 3.3 et 3.12, on a défini une application
Remarque.
Dans [Reference Moeglin and Waldspurger6], l’application
![]() ${\mathcal{Q}}(d^{\prime },d^{\prime \prime })^{\operatorname{Lie}}$
est simplement notée
${\mathcal{Q}}(d^{\prime },d^{\prime \prime })^{\operatorname{Lie}}$
est simplement notée
![]() ${\mathcal{Q}}^{\operatorname{Lie}}$
. On a précisé ici la notation en insérant le couple
${\mathcal{Q}}^{\operatorname{Lie}}$
. On a précisé ici la notation en insérant le couple
![]() $(d^{\prime },d^{\prime \prime })$
.
$(d^{\prime },d^{\prime \prime })$
.
Fixons
![]() $w^{\prime }\in \mathfrak{S}_{d^{\prime }}$
et
$w^{\prime }\in \mathfrak{S}_{d^{\prime }}$
et
![]() $w^{\prime \prime }\in \mathfrak{S}_{d^{\prime \prime }}$
dont les classes de conjugaison sont paramétrées par des partitions dont tous les termes non nuls sont impairs. On note
$w^{\prime \prime }\in \mathfrak{S}_{d^{\prime \prime }}$
dont les classes de conjugaison sont paramétrées par des partitions dont tous les termes non nuls sont impairs. On note
![]() $\unicode[STIX]{x1D711}_{w^{\prime }}$
et
$\unicode[STIX]{x1D711}_{w^{\prime }}$
et
![]() $\unicode[STIX]{x1D711}_{w^{\prime \prime }}$
les fonctions caractéristiques de ces classes de conjugaison. On pose
$\unicode[STIX]{x1D711}_{w^{\prime \prime }}$
les fonctions caractéristiques de ces classes de conjugaison. On pose
Soit
![]() $(d_{1},d_{2})\in D(d)$
. Ce couple détermine une donnée endoscopique de
$(d_{1},d_{2})\in D(d)$
. Ce couple détermine une donnée endoscopique de
![]() $G_{\operatorname{iso}}$
et
$G_{\operatorname{iso}}$
et
![]() $G_{\operatorname{an}}$
. Le groupe endoscopique de cette donnée est
$G_{\operatorname{an}}$
. Le groupe endoscopique de cette donnée est
![]() $G_{d_{1},\operatorname{iso}}\times G_{d_{2},\operatorname{iso}}$
. Il y a un transfert de
$G_{d_{1},\operatorname{iso}}\times G_{d_{2},\operatorname{iso}}$
. Il y a un transfert de
![]() $C_{\operatorname{cusp}}^{\infty }(\mathfrak{g}_{\operatorname{iso}}(E^{\natural }))\oplus C_{\operatorname{cusp}}^{\infty }(\mathfrak{g}_{\operatorname{an}}(E^{\natural }))$
dans
$C_{\operatorname{cusp}}^{\infty }(\mathfrak{g}_{\operatorname{iso}}(E^{\natural }))\oplus C_{\operatorname{cusp}}^{\infty }(\mathfrak{g}_{\operatorname{an}}(E^{\natural }))$
dans
 $$\begin{eqnarray}\displaystyle & & \displaystyle \left(C_{\operatorname{cusp}}^{\infty }(\mathfrak{g}_{d_{1},\operatorname{iso}}(E^{\natural }))\oplus C_{\operatorname{cusp}}^{\infty }(\mathfrak{g}_{d_{1},\operatorname{an}}(E^{\natural }))\right)\nonumber\\ \displaystyle & & \displaystyle \quad \otimes \left(C_{\operatorname{cusp}}^{\infty }(\mathfrak{g}_{d_{2},\operatorname{iso}}(E^{\natural }))\oplus C_{\operatorname{cusp}}^{\infty }(\mathfrak{g}_{d_{2},\operatorname{an}}(E^{\natural }))\right).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \left(C_{\operatorname{cusp}}^{\infty }(\mathfrak{g}_{d_{1},\operatorname{iso}}(E^{\natural }))\oplus C_{\operatorname{cusp}}^{\infty }(\mathfrak{g}_{d_{1},\operatorname{an}}(E^{\natural }))\right)\nonumber\\ \displaystyle & & \displaystyle \quad \otimes \left(C_{\operatorname{cusp}}^{\infty }(\mathfrak{g}_{d_{2},\operatorname{iso}}(E^{\natural }))\oplus C_{\operatorname{cusp}}^{\infty }(\mathfrak{g}_{d_{2},\operatorname{an}}(E^{\natural }))\right).\nonumber\end{eqnarray}$$
On le note
![]() $\text{transfert}_{d_{1},d_{2}}$
. Il y a un choix naturel de facteur de transfert, cf. [Reference Waldspurger9] proposition X.8. Comme précédemment, on supprime les discriminants de Weyl. Le
$\text{transfert}_{d_{1},d_{2}}$
. Il y a un choix naturel de facteur de transfert, cf. [Reference Waldspurger9] proposition X.8. Comme précédemment, on supprime les discriminants de Weyl. Le
![]() $\unicode[STIX]{x1D702}$
de la définition X.7 de [Reference Waldspurger9] est une unité de
$\unicode[STIX]{x1D702}$
de la définition X.7 de [Reference Waldspurger9] est une unité de
![]() $E^{\natural }$
si
$E^{\natural }$
si
![]() $d$
est impair, une unité de
$d$
est impair, une unité de
![]() $E$
de trace nulle dans
$E$
de trace nulle dans
![]() $E^{\natural }$
si
$E^{\natural }$
si
![]() $d$
est pair.
$d$
est pair.
Dans le cas où
![]() $(d_{1},d_{2})=(d^{\prime },d^{\prime \prime })$
, on peut appliquer la construction ci-dessus en remplaçant
$(d_{1},d_{2})=(d^{\prime },d^{\prime \prime })$
, on peut appliquer la construction ci-dessus en remplaçant
![]() $d$
par
$d$
par
![]() $d^{\prime }$
, respectivement
$d^{\prime }$
, respectivement
![]() $d^{\prime \prime }$
, et
$d^{\prime \prime }$
, et
![]() $(d^{\prime },d^{\prime \prime })$
par
$(d^{\prime },d^{\prime \prime })$
par
![]() $(d^{\prime },0)$
, respectivement
$(d^{\prime },0)$
, respectivement
![]() $(d^{\prime \prime },0)$
. On définit ainsi
$(d^{\prime \prime },0)$
. On définit ainsi
Lemme.
(i) On a l’égalité
 $\text{transfert}_{d^{\prime },d^{\prime \prime }}(f)=f_{1}\,\otimes \,f_{2}$
.
$\text{transfert}_{d^{\prime },d^{\prime \prime }}(f)=f_{1}\,\otimes \,f_{2}$
.(ii) Pour un couple
 $(d_{1},d_{2})\in D(d)$
différent de
$(d_{1},d_{2})\in D(d)$
différent de
 $(d^{\prime },d^{\prime \prime })$
, on a l’égalité
$(d^{\prime },d^{\prime \prime })$
, on a l’égalité
 $\text{transfert}_{d_{1},d_{2}}(f)=0$
.
$\text{transfert}_{d_{1},d_{2}}(f)=0$
.
2.4 Une expression à l’aide de transformées de Fourier d’intégrales orbitales
On commence la démonstration du lemme 2.2. On utilise les notations de ce paragraphe et les données que l’on y a fixées. Rappelons que pour
![]() $\sharp =\operatorname{iso}$
ou
$\sharp =\operatorname{iso}$
ou
![]() $\operatorname{an}$
, on définit dans l’espace
$\operatorname{an}$
, on définit dans l’espace
![]() $\mathfrak{g}_{\sharp }(F)$
la notion d’élément topologiquement nilpotent. En identifiant
$\mathfrak{g}_{\sharp }(F)$
la notion d’élément topologiquement nilpotent. En identifiant
![]() $\mathfrak{g}_{\sharp }(F)$
à un sous-ensemble de l’algèbre des endomorphismes de
$\mathfrak{g}_{\sharp }(F)$
à un sous-ensemble de l’algèbre des endomorphismes de
![]() $V_{\sharp }$
, un élément
$V_{\sharp }$
, un élément
![]() $Y\in \mathfrak{g}_{\sharp }(F)$
est topologiquement nilpotent si et seulement si la suite des puissances
$Y\in \mathfrak{g}_{\sharp }(F)$
est topologiquement nilpotent si et seulement si la suite des puissances
![]() $Y^{m}$
tend vers
$Y^{m}$
tend vers
![]() $0$
quand
$0$
quand
![]() $m$
tend vers l’infini. Par construction de l’application
$m$
tend vers l’infini. Par construction de l’application
![]() ${\mathcal{Q}}(r^{\prime },r^{\prime \prime })^{\operatorname{Lie}}$
, la fonction
${\mathcal{Q}}(r^{\prime },r^{\prime \prime })^{\operatorname{Lie}}$
, la fonction
![]() $f$
est à support topologiquement nilpotent.
$f$
est à support topologiquement nilpotent.
On note
![]() $(\emptyset ,\unicode[STIX]{x1D6FD}^{\prime })$
et
$(\emptyset ,\unicode[STIX]{x1D6FD}^{\prime })$
et
![]() $(\emptyset ,\unicode[STIX]{x1D6FD}^{\prime \prime })$
les couples de partitions paramétrant les classes de conjugaison de
$(\emptyset ,\unicode[STIX]{x1D6FD}^{\prime \prime })$
les couples de partitions paramétrant les classes de conjugaison de
![]() $w^{\prime }$
et
$w^{\prime }$
et
![]() $w^{\prime \prime }$
. Posons
$w^{\prime \prime }$
. Posons
![]() $\unicode[STIX]{x1D6FD}=\unicode[STIX]{x1D6FD}^{\prime }\cup \unicode[STIX]{x1D6FD}^{\prime \prime }$
,
$\unicode[STIX]{x1D6FD}=\unicode[STIX]{x1D6FD}^{\prime }\cup \unicode[STIX]{x1D6FD}^{\prime \prime }$
,
![]() $\unicode[STIX]{x1D6FD}=(\unicode[STIX]{x1D6FD}_{1}\geqslant \cdots \geqslant \unicode[STIX]{x1D6FD}_{t}>0)$
. Pour tout
$\unicode[STIX]{x1D6FD}=(\unicode[STIX]{x1D6FD}_{1}\geqslant \cdots \geqslant \unicode[STIX]{x1D6FD}_{t}>0)$
. Pour tout
![]() $k\in \{1,\ldots ,t\}$
, considérons la tour d’extensions non ramifiées
$k\in \{1,\ldots ,t\}$
, considérons la tour d’extensions non ramifiées
![]() $E_{k}/E_{k}^{\natural }/F$
telle que
$E_{k}/E_{k}^{\natural }/F$
telle que
![]() $[E_{k}:E_{k}^{\natural }]=2$
et
$[E_{k}:E_{k}^{\natural }]=2$
et
![]() $[E_{k}^{\natural }:F]=\unicode[STIX]{x1D6FD}_{k}$
. On fixe un élément
$[E_{k}^{\natural }:F]=\unicode[STIX]{x1D6FD}_{k}$
. On fixe un élément
![]() $X_{k}\in E_{k}^{\times }$
tel que
$X_{k}\in E_{k}^{\times }$
tel que
![]() $\operatorname{val}_{E_{k}}(X_{k})=0$
, que
$\operatorname{val}_{E_{k}}(X_{k})=0$
, que
![]() $\operatorname{trace}_{E_{k}/E_{k}^{\natural }}(X_{k})=0$
et que, en notant
$\operatorname{trace}_{E_{k}/E_{k}^{\natural }}(X_{k})=0$
et que, en notant
![]() $\bar{X}_{k}$
la réduction de
$\bar{X}_{k}$
la réduction de
![]() $X_{k}$
dans le corps résiduel
$X_{k}$
dans le corps résiduel
![]() $\mathbb{F}_{q^{2\unicode[STIX]{x1D6FD}_{k}}}$
, tous les conjugués de
$\mathbb{F}_{q^{2\unicode[STIX]{x1D6FD}_{k}}}$
, tous les conjugués de
![]() $\bar{X}_{k}$
par le groupe de Galois de l’extension
$\bar{X}_{k}$
par le groupe de Galois de l’extension
![]() $\mathbb{F}_{q^{2\unicode[STIX]{x1D6FD}_{k}}}/\mathbb{F}_{q}$
soient distincts. On suppose de plus que, pour
$\mathbb{F}_{q^{2\unicode[STIX]{x1D6FD}_{k}}}/\mathbb{F}_{q}$
soient distincts. On suppose de plus que, pour
![]() $k,k^{\prime }\in \{1,\ldots ,t\}$
avec
$k,k^{\prime }\in \{1,\ldots ,t\}$
avec
![]() $k\not =k^{\prime }$
,
$k\not =k^{\prime }$
,
![]() $\bar{X}_{k}$
n’est pas conjugué à
$\bar{X}_{k}$
n’est pas conjugué à
![]() $\bar{X}_{k^{\prime }}$
. Cette hypothèse est loisible puisque
$\bar{X}_{k^{\prime }}$
. Cette hypothèse est loisible puisque
![]() $p>6n+4$
.
$p>6n+4$
.
Posons
![]() $R=\sup (r^{\prime },r^{\prime \prime })$
,
$R=\sup (r^{\prime },r^{\prime \prime })$
,
![]() $r=\text{inf}(r^{\prime },r^{\prime \prime })$
,
$r=\text{inf}(r^{\prime },r^{\prime \prime })$
,
![]() $J=\{1,\ldots ,R\}$
,
$J=\{1,\ldots ,R\}$
,
![]() ${\hat{J}}=\{j\in J;j\leqslant R-r,j\,\,\operatorname{pair}\}$
. Fixons un ensemble de représentants
${\hat{J}}=\{j\in J;j\leqslant R-r,j\,\,\operatorname{pair}\}$
. Fixons un ensemble de représentants
![]() $\unicode[STIX]{x1D6E4}_{0}$
de
$\unicode[STIX]{x1D6E4}_{0}$
de
![]() $\mathfrak{o}^{\times }/(1+\unicode[STIX]{x1D71B}\mathfrak{o})$
. Pour tout
$\mathfrak{o}^{\times }/(1+\unicode[STIX]{x1D71B}\mathfrak{o})$
. Pour tout
![]() $j\in J$
tel que
$j\in J$
tel que
![]() $j>R-r$
, fixons un ensemble de représentants
$j>R-r$
, fixons un ensemble de représentants
![]() $\unicode[STIX]{x1D6E4}_{j}$
de
$\unicode[STIX]{x1D6E4}_{j}$
de
![]() $\mathfrak{o}^{\times }/\mathfrak{o}^{\times 2}$
. Pour tout
$\mathfrak{o}^{\times }/\mathfrak{o}^{\times 2}$
. Pour tout
![]() $j\in J$
tel que
$j\in J$
tel que
![]() $j\leqslant R-r$
, posons
$j\leqslant R-r$
, posons
![]() $\unicode[STIX]{x1D6E4}_{j}=\unicode[STIX]{x1D6E4}_{0}$
. Notons
$\unicode[STIX]{x1D6E4}_{j}=\unicode[STIX]{x1D6E4}_{0}$
. Notons
![]() $\unicode[STIX]{x1D6E4}$
le sous-ensemble des
$\unicode[STIX]{x1D6E4}$
le sous-ensemble des
![]() $\unicode[STIX]{x1D6FE}=(\unicode[STIX]{x1D6FE}_{j})_{j\in J}\in \prod _{j\in J}\unicode[STIX]{x1D6E4}_{j}$
tels que
$\unicode[STIX]{x1D6FE}=(\unicode[STIX]{x1D6FE}_{j})_{j\in J}\in \prod _{j\in J}\unicode[STIX]{x1D6E4}_{j}$
tels que
pour tout
![]() $j\in {\hat{J}}$
,
$j\in {\hat{J}}$
,
![]() $\unicode[STIX]{x1D6FE}_{j-1}\not \in \unicode[STIX]{x1D6FE}_{j}+\unicode[STIX]{x1D71B}\mathfrak{o}$
;
$\unicode[STIX]{x1D6FE}_{j-1}\not \in \unicode[STIX]{x1D6FE}_{j}+\unicode[STIX]{x1D71B}\mathfrak{o}$
;
(1)
![]() $\operatorname{sgn}(\unicode[STIX]{x1D702}\unicode[STIX]{x1D71B}^{-\operatorname{val}_{F}(\unicode[STIX]{x1D702})}\prod _{j\in J}\unicode[STIX]{x1D6FE}_{j})=\operatorname{sgn}_{CD}(w^{\prime })\operatorname{sgn}_{CD}(w^{\prime \prime })$
.
$\operatorname{sgn}(\unicode[STIX]{x1D702}\unicode[STIX]{x1D71B}^{-\operatorname{val}_{F}(\unicode[STIX]{x1D702})}\prod _{j\in J}\unicode[STIX]{x1D6FE}_{j})=\operatorname{sgn}_{CD}(w^{\prime })\operatorname{sgn}_{CD}(w^{\prime \prime })$
.
Remarques.
L’ensemble
![]() $\unicode[STIX]{x1D6E4}$
n’a évidemment rien à voir avec celui de [Reference Waldspurger11] 1.8. D’autre part, dans le cas où
$\unicode[STIX]{x1D6E4}$
n’a évidemment rien à voir avec celui de [Reference Waldspurger11] 1.8. D’autre part, dans le cas où
![]() $r^{\prime }=r^{\prime \prime }=0$
, on a
$r^{\prime }=r^{\prime \prime }=0$
, on a
![]() $J=\emptyset$
et
$J=\emptyset$
et
![]() $\prod _{j\in J}\unicode[STIX]{x1D6E4}_{j}$
a un unique élément. Cet élément vérifie (1) si et seulement si
$\prod _{j\in J}\unicode[STIX]{x1D6E4}_{j}$
a un unique élément. Cet élément vérifie (1) si et seulement si
![]() $\operatorname{sgn}(\unicode[STIX]{x1D702}\unicode[STIX]{x1D71B}^{-\operatorname{val}_{F}(\unicode[STIX]{x1D702})})=\operatorname{sgn}_{CD}(w^{\prime })\operatorname{sgn}_{CD}(w^{\prime \prime })$
. Donc
$\operatorname{sgn}(\unicode[STIX]{x1D702}\unicode[STIX]{x1D71B}^{-\operatorname{val}_{F}(\unicode[STIX]{x1D702})})=\operatorname{sgn}_{CD}(w^{\prime })\operatorname{sgn}_{CD}(w^{\prime \prime })$
. Donc
![]() $\unicode[STIX]{x1D6E4}$
est vide si cette égalité n’est pas vérifiée. Dans l’égalité du lemme ci-dessous, le membre de droite est nul. Cela est cohérent avec la remarque de 2.2 nous disant que
$\unicode[STIX]{x1D6E4}$
est vide si cette égalité n’est pas vérifiée. Dans l’égalité du lemme ci-dessous, le membre de droite est nul. Cela est cohérent avec la remarque de 2.2 nous disant que
![]() $f_{\sharp }=0$
.
$f_{\sharp }=0$
.
On note
![]() $\unicode[STIX]{x1D70E}:\unicode[STIX]{x1D6E4}\rightarrow \mathbb{C}$
la fonction définie par
$\unicode[STIX]{x1D70E}:\unicode[STIX]{x1D6E4}\rightarrow \mathbb{C}$
la fonction définie par
 $$\begin{eqnarray}\displaystyle & \unicode[STIX]{x1D70E}(\unicode[STIX]{x1D6FE})=\left(\displaystyle \mathop{\prod }_{j\in {\hat{J}}}(q-2+\operatorname{sgn}(\unicode[STIX]{x1D6FE}_{j-1}\unicode[STIX]{x1D6FE}_{j}))\operatorname{sgn}(\unicode[STIX]{x1D6FE}_{j-1}\unicode[STIX]{x1D6FE}_{j}(\unicode[STIX]{x1D6FE}_{j-1}-\unicode[STIX]{x1D6FE}_{j}))\right) & \displaystyle \nonumber\\ \displaystyle & \displaystyle \mathop{\prod }_{j=R-r+1,\ldots ,R;\,j\,\,\operatorname{impair}}\operatorname{sgn}(-\unicode[STIX]{x1D6FE}_{j}). & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \unicode[STIX]{x1D70E}(\unicode[STIX]{x1D6FE})=\left(\displaystyle \mathop{\prod }_{j\in {\hat{J}}}(q-2+\operatorname{sgn}(\unicode[STIX]{x1D6FE}_{j-1}\unicode[STIX]{x1D6FE}_{j}))\operatorname{sgn}(\unicode[STIX]{x1D6FE}_{j-1}\unicode[STIX]{x1D6FE}_{j}(\unicode[STIX]{x1D6FE}_{j-1}-\unicode[STIX]{x1D6FE}_{j}))\right) & \displaystyle \nonumber\\ \displaystyle & \displaystyle \mathop{\prod }_{j=R-r+1,\ldots ,R;\,j\,\,\operatorname{impair}}\operatorname{sgn}(-\unicode[STIX]{x1D6FE}_{j}). & \displaystyle \nonumber\end{eqnarray}$$
Notons
![]() $\bar{F}$
une clôture algébrique de
$\bar{F}$
une clôture algébrique de
![]() $F$
. Pour
$F$
. Pour
![]() $\unicode[STIX]{x1D6FE}\in \unicode[STIX]{x1D6E4}$
et pour
$\unicode[STIX]{x1D6FE}\in \unicode[STIX]{x1D6E4}$
et pour
![]() $j\in J$
, on fixe
$j\in J$
, on fixe
![]() $a_{j}(\unicode[STIX]{x1D6FE})\in \bar{F}^{\times }$
tel que
$a_{j}(\unicode[STIX]{x1D6FE})\in \bar{F}^{\times }$
tel que
si
![]() $j\in {\hat{J}}$
,
$j\in {\hat{J}}$
,
![]() $a_{j}(\unicode[STIX]{x1D6FE})^{2j-2}=\unicode[STIX]{x1D71B}\unicode[STIX]{x1D6FE}_{j}$
;
$a_{j}(\unicode[STIX]{x1D6FE})^{2j-2}=\unicode[STIX]{x1D71B}\unicode[STIX]{x1D6FE}_{j}$
;
si
![]() $j\leqslant R-r$
et
$j\leqslant R-r$
et
![]() $j$
est impair,
$j$
est impair,
![]() $a_{j}(\unicode[STIX]{x1D6FE})^{2j}=\unicode[STIX]{x1D71B}\unicode[STIX]{x1D6FE}_{j}$
;
$a_{j}(\unicode[STIX]{x1D6FE})^{2j}=\unicode[STIX]{x1D71B}\unicode[STIX]{x1D6FE}_{j}$
;
si
![]() $j>R-r$
,
$j>R-r$
,
![]() $a_{j}(\unicode[STIX]{x1D6FE})^{2(2j-R+r-1)}=\unicode[STIX]{x1D71B}\unicode[STIX]{x1D6FE}_{j}$
. On note
$a_{j}(\unicode[STIX]{x1D6FE})^{2(2j-R+r-1)}=\unicode[STIX]{x1D71B}\unicode[STIX]{x1D6FE}_{j}$
. On note
![]() $F_{j}(\unicode[STIX]{x1D6FE})$
l’extension
$F_{j}(\unicode[STIX]{x1D6FE})$
l’extension
![]() $F[a_{j}(\unicode[STIX]{x1D6FE})]$
,
$F[a_{j}(\unicode[STIX]{x1D6FE})]$
,
![]() $F_{j}^{\natural }(\unicode[STIX]{x1D6FE})=F[a_{j}(\unicode[STIX]{x1D6FE})^{2}]$
la sous-extension d’indice
$F_{j}^{\natural }(\unicode[STIX]{x1D6FE})=F[a_{j}(\unicode[STIX]{x1D6FE})^{2}]$
la sous-extension d’indice
![]() $2$
,
$2$
,
![]() $\mathfrak{p}_{j}(\unicode[STIX]{x1D6FE})$
l’idéal maximal de l’anneau des entiers de
$\mathfrak{p}_{j}(\unicode[STIX]{x1D6FE})$
l’idéal maximal de l’anneau des entiers de
![]() $F_{j}(\unicode[STIX]{x1D6FE})$
et
$F_{j}(\unicode[STIX]{x1D6FE})$
et
On pose
![]() $A(\unicode[STIX]{x1D6FE})=\prod _{j\in J}A_{j}(\unicode[STIX]{x1D6FE})$
. Remarquons que
$A(\unicode[STIX]{x1D6FE})=\prod _{j\in J}A_{j}(\unicode[STIX]{x1D6FE})$
. Remarquons que
![]() $A(\unicode[STIX]{x1D6FE})$
est naturellement un espace principal homogène sous un certain groupe. On munit
$A(\unicode[STIX]{x1D6FE})$
est naturellement un espace principal homogène sous un certain groupe. On munit
![]() $A(\unicode[STIX]{x1D6FE})$
d’une mesure invariante par l’action de ce groupe et de masse totale
$A(\unicode[STIX]{x1D6FE})$
d’une mesure invariante par l’action de ce groupe et de masse totale
![]() $1$
.
$1$
.
Considérons des éléments
![]() $\unicode[STIX]{x1D6FE}\in \unicode[STIX]{x1D6E4}$
et
$\unicode[STIX]{x1D6FE}\in \unicode[STIX]{x1D6E4}$
et
![]() $a=(a_{j})_{j\in J}\in A(\unicode[STIX]{x1D6FE})$
. Considérons des familles
$a=(a_{j})_{j\in J}\in A(\unicode[STIX]{x1D6FE})$
. Considérons des familles
![]() $c=(c_{j})_{j\in J}$
et
$c=(c_{j})_{j\in J}$
et
![]() $u=(u_{k})_{k=1,\ldots ,t}$
telles que
$u=(u_{k})_{k=1,\ldots ,t}$
telles que
![]() $c_{j}\in F_{j}^{\natural }(\unicode[STIX]{x1D6FE})^{\times }$
pour
$c_{j}\in F_{j}^{\natural }(\unicode[STIX]{x1D6FE})^{\times }$
pour
![]() $j\in J$
et
$j\in J$
et
![]() $u_{k}\in E_{k}^{\natural ,\times }$
pour
$u_{k}\in E_{k}^{\natural ,\times }$
pour
![]() $k=1,\ldots ,t$
. Pour
$k=1,\ldots ,t$
. Pour
![]() $j\in J$
, on construit un espace quadratique
$j\in J$
, on construit un espace quadratique
![]() $(V_{j},Q_{j})$
:
$(V_{j},Q_{j})$
:
![]() $V_{j}=F_{j}(\unicode[STIX]{x1D6FE})$
et, pour
$V_{j}=F_{j}(\unicode[STIX]{x1D6FE})$
et, pour
![]() $v,v^{\prime }\in V_{j}$
,
$v,v^{\prime }\in V_{j}$
,
![]() $Q_{j}(v,v^{\prime })=[F_{j}(\unicode[STIX]{x1D6FE})/F]^{-1}\operatorname{trace}_{F_{j}(\unicode[STIX]{x1D6FE})/F}(\unicode[STIX]{x1D70F}_{j}(v)v^{\prime }c_{j})$
, où
$Q_{j}(v,v^{\prime })=[F_{j}(\unicode[STIX]{x1D6FE})/F]^{-1}\operatorname{trace}_{F_{j}(\unicode[STIX]{x1D6FE})/F}(\unicode[STIX]{x1D70F}_{j}(v)v^{\prime }c_{j})$
, où
![]() $\unicode[STIX]{x1D70F}_{j}$
est l’unique élément non trivial du groupe de Galois de
$\unicode[STIX]{x1D70F}_{j}$
est l’unique élément non trivial du groupe de Galois de
![]() $F_{j}(\unicode[STIX]{x1D6FE})/F_{j}^{\natural }(\unicode[STIX]{x1D6FE})$
. Pour
$F_{j}(\unicode[STIX]{x1D6FE})/F_{j}^{\natural }(\unicode[STIX]{x1D6FE})$
. Pour
![]() $k=1,\ldots ,t$
, on construit un espace quadratique
$k=1,\ldots ,t$
, on construit un espace quadratique
![]() $(V_{k},Q_{k})$
:
$(V_{k},Q_{k})$
:
![]() $V_{k}=E_{k}$
et, pour
$V_{k}=E_{k}$
et, pour
![]() $v,v^{\prime }\in V_{k}$
,
$v,v^{\prime }\in V_{k}$
,
![]() $Q_{k}(v,v^{\prime })=[E_{k}/F]^{-1}\operatorname{trace}_{E_{k}/F}(\unicode[STIX]{x1D70F}_{k}(v)v^{\prime }u_{k})$
, où
$Q_{k}(v,v^{\prime })=[E_{k}/F]^{-1}\operatorname{trace}_{E_{k}/F}(\unicode[STIX]{x1D70F}_{k}(v)v^{\prime }u_{k})$
, où
![]() $\unicode[STIX]{x1D70F}_{k}$
est l’unique élément non trivial du groupe de Galois de
$\unicode[STIX]{x1D70F}_{k}$
est l’unique élément non trivial du groupe de Galois de
![]() $E_{k}/E_{k}^{\natural }$
. En utilisant la relation
$E_{k}/E_{k}^{\natural }$
. En utilisant la relation
![]() $r^{\prime }\equiv r^{\prime \prime }\equiv \operatorname{val}_{F}(\unicode[STIX]{x1D702})$
imposée en 2.2 et la relation (1) ci-dessus, on montre que la somme directe des
$r^{\prime }\equiv r^{\prime \prime }\equiv \operatorname{val}_{F}(\unicode[STIX]{x1D702})$
imposée en 2.2 et la relation (1) ci-dessus, on montre que la somme directe des
![]() $(V_{j},Q_{j})$
et des
$(V_{j},Q_{j})$
et des
![]() $(V_{k},Q_{k})$
est isomorphe à l’un des deux espaces de 2.2, disons à
$(V_{k},Q_{k})$
est isomorphe à l’un des deux espaces de 2.2, disons à
![]() $(V_{\sharp },Q_{\sharp })$
. On fixe un isomorphisme. On définit alors un élément
$(V_{\sharp },Q_{\sharp })$
. On fixe un isomorphisme. On définit alors un élément
![]() $X\in \mathfrak{g}_{\sharp }(F)$
: il respecte chacun des sous-espaces
$X\in \mathfrak{g}_{\sharp }(F)$
: il respecte chacun des sous-espaces
![]() $V_{j}$
et
$V_{j}$
et
![]() $V_{k}$
; pour
$V_{k}$
; pour
![]() $j\in J$
, il agit sur
$j\in J$
, il agit sur
![]() $V_{j}$
par multiplication par
$V_{j}$
par multiplication par
![]() $a_{j}$
et, pour
$a_{j}$
et, pour
![]() $k=1,\ldots ,t$
, il agit sur
$k=1,\ldots ,t$
, il agit sur
![]() $V_{k}$
par multiplication par
$V_{k}$
par multiplication par
![]() $X_{k}$
. La classe de conjugaison de
$X_{k}$
. La classe de conjugaison de
![]() $X$
par le groupe orthogonal
$X$
par le groupe orthogonal
![]() $O(Q_{\sharp };F)$
est bien déterminée par nos données de départ. Il y a une petite difficulté causée par la parité de la dimension de
$O(Q_{\sharp };F)$
est bien déterminée par nos données de départ. Il y a une petite difficulté causée par la parité de la dimension de
![]() $V_{\sharp }$
: cette classe de conjugaison par
$V_{\sharp }$
: cette classe de conjugaison par
![]() $O(Q_{\sharp };F)$
se décompose en deux classes de conjugaison par
$O(Q_{\sharp };F)$
se décompose en deux classes de conjugaison par
![]() $G_{\sharp }(F)$
. Au lieu de
$G_{\sharp }(F)$
. Au lieu de
![]() $X$
, nous fixons donc des éléments
$X$
, nous fixons donc des éléments
![]() $X^{+}$
et
$X^{+}$
et
![]() $X^{-}$
dans chacune de ces deux classes. On voit facilement que les constructions ne dépendent que des images des
$X^{-}$
dans chacune de ces deux classes. On voit facilement que les constructions ne dépendent que des images des
![]() $c_{j}$
dans les groupes
$c_{j}$
dans les groupes
![]() $F_{j}^{\natural }(\unicode[STIX]{x1D6FE})^{\times }/\operatorname{norme}_{F_{j}(\unicode[STIX]{x1D6FE})/F_{j}^{\natural }(\unicode[STIX]{x1D6FE})}(F_{j}(\unicode[STIX]{x1D6FE})^{\times })$
et des images des
$F_{j}^{\natural }(\unicode[STIX]{x1D6FE})^{\times }/\operatorname{norme}_{F_{j}(\unicode[STIX]{x1D6FE})/F_{j}^{\natural }(\unicode[STIX]{x1D6FE})}(F_{j}(\unicode[STIX]{x1D6FE})^{\times })$
et des images des
![]() $u_{k}$
dans les groupes
$u_{k}$
dans les groupes
![]() $E_{k}^{\natural ,\times }/\operatorname{norme}_{E_{k}/E_{k}^{\natural }}(E_{k}^{\times })$
. Parce que les
$E_{k}^{\natural ,\times }/\operatorname{norme}_{E_{k}/E_{k}^{\natural }}(E_{k}^{\times })$
. Parce que les
![]() $F_{j}(\unicode[STIX]{x1D6FE})/F$
sont totalement ramifiés et les
$F_{j}(\unicode[STIX]{x1D6FE})/F$
sont totalement ramifiés et les
![]() $E_{k}/F$
sont non ramifiés, ces groupes s’identifient respectivement à
$E_{k}/F$
sont non ramifiés, ces groupes s’identifient respectivement à
![]() $\mathfrak{o}^{\times }/\mathfrak{o}^{\times 2}$
et
$\mathfrak{o}^{\times }/\mathfrak{o}^{\times 2}$
et
![]() $\mathbb{Z}/2\mathbb{Z}$
. En posant
$\mathbb{Z}/2\mathbb{Z}$
. En posant
![]() ${\mathcal{E}}=(\mathfrak{o}^{\times }/\mathfrak{o}^{\times 2})^{J}$
et
${\mathcal{E}}=(\mathfrak{o}^{\times }/\mathfrak{o}^{\times 2})^{J}$
et
![]() ${\mathcal{U}}=(\mathbb{Z}/2\mathbb{Z})^{t}$
, on peut donc remplacer les données
${\mathcal{U}}=(\mathbb{Z}/2\mathbb{Z})^{t}$
, on peut donc remplacer les données
![]() $c=(c_{j})_{j\in J}$
et
$c=(c_{j})_{j\in J}$
et
![]() $u=(u_{k})_{k=1,\ldots ,t}$
ci-dessus par des familles
$u=(u_{k})_{k=1,\ldots ,t}$
ci-dessus par des familles
![]() $c=(c_{j})_{j\in J}\in {\mathcal{E}}$
et
$c=(c_{j})_{j\in J}\in {\mathcal{E}}$
et
![]() $u=(u_{k})_{k=1,\ldots ,t}\in {\mathcal{U}}$
. Notons plus précisément
$u=(u_{k})_{k=1,\ldots ,t}\in {\mathcal{U}}$
. Notons plus précisément
![]() $X^{+}(a,c,u)$
et
$X^{+}(a,c,u)$
et
![]() $X^{-}(a,c,u)$
les éléments associés ci-dessus à de telles familles.
$X^{-}(a,c,u)$
les éléments associés ci-dessus à de telles familles.
Soit
![]() $\unicode[STIX]{x1D6FE}\in \unicode[STIX]{x1D6E4}$
et
$\unicode[STIX]{x1D6FE}\in \unicode[STIX]{x1D6E4}$
et
![]() $e\in {\mathcal{E}}$
. On définit une nouvelle famille
$e\in {\mathcal{E}}$
. On définit une nouvelle famille
![]() $c[\unicode[STIX]{x1D6FE},e]=(c[\unicode[STIX]{x1D6FE},e]_{j})_{j\in J}\in {\mathcal{E}}$
par les égalités suivantes, pour
$c[\unicode[STIX]{x1D6FE},e]=(c[\unicode[STIX]{x1D6FE},e]_{j})_{j\in J}\in {\mathcal{E}}$
par les égalités suivantes, pour
![]() $j\in J$
:
$j\in J$
:
si
![]() $r^{\prime \prime }\leqslant r^{\prime }$
,
$r^{\prime \prime }\leqslant r^{\prime }$
,
![]() $c[\unicode[STIX]{x1D6FE},e]_{j}=(-1)^{j}\unicode[STIX]{x1D6FE}_{j}e_{j}$
;
$c[\unicode[STIX]{x1D6FE},e]_{j}=(-1)^{j}\unicode[STIX]{x1D6FE}_{j}e_{j}$
;
si
![]() $r^{\prime }<r^{\prime \prime }$
,
$r^{\prime }<r^{\prime \prime }$
,
![]() $c[\unicode[STIX]{x1D6FE},e]_{j}=(-1)^{j+1}e_{j}$
$c[\unicode[STIX]{x1D6FE},e]_{j}=(-1)^{j+1}e_{j}$
(il s’agit plutôt des images modulo
![]() $\mathfrak{o}^{\times 2}$
des expressions indiquées). Pour
$\mathfrak{o}^{\times 2}$
des expressions indiquées). Pour
![]() $a\in A(\unicode[STIX]{x1D6FE})$
et
$a\in A(\unicode[STIX]{x1D6FE})$
et
![]() $\unicode[STIX]{x1D701}=\pm$
, on note désormais
$\unicode[STIX]{x1D701}=\pm$
, on note désormais
![]() $X^{\unicode[STIX]{x1D701}}(a,e,u)$
l’élément
$X^{\unicode[STIX]{x1D701}}(a,e,u)$
l’élément
![]() $X^{\unicode[STIX]{x1D701}}(a,c[\unicode[STIX]{x1D6FE},e],u)$
introduit ci-dessus. Il appartient à
$X^{\unicode[STIX]{x1D701}}(a,c[\unicode[STIX]{x1D6FE},e],u)$
introduit ci-dessus. Il appartient à
![]() $\mathfrak{g}_{\sharp }(F)$
pour un certain indice
$\mathfrak{g}_{\sharp }(F)$
pour un certain indice
![]() $\sharp$
, que l’on note plus précisement
$\sharp$
, que l’on note plus précisement
![]() $\sharp (a,e,u)$
.
$\sharp (a,e,u)$
.
Soit
![]() $\sharp =\operatorname{iso}$
ou
$\sharp =\operatorname{iso}$
ou
![]() $\operatorname{an}$
. De même qu’en 1.1, on introduit une transformation de Fourier dans
$\operatorname{an}$
. De même qu’en 1.1, on introduit une transformation de Fourier dans
![]() $C_{c}^{\infty }(\mathfrak{g}_{\sharp }(F))$
. Rappelons un résultat d’Harish-Chandra. Soit
$C_{c}^{\infty }(\mathfrak{g}_{\sharp }(F))$
. Rappelons un résultat d’Harish-Chandra. Soit
![]() $X\in \mathfrak{g}_{\sharp }(F)$
un élément régulier et elliptique. Il existe une fonction
$X\in \mathfrak{g}_{\sharp }(F)$
un élément régulier et elliptique. Il existe une fonction
![]() $Y\mapsto \hat{i} _{\sharp }(X,Y)$
définie et localement constante sur l’ensemble des éléments elliptiques réguliers de
$Y\mapsto \hat{i} _{\sharp }(X,Y)$
définie et localement constante sur l’ensemble des éléments elliptiques réguliers de
![]() $\mathfrak{g}_{\sharp }(F)$
de sorte que, pour tout tel élément
$\mathfrak{g}_{\sharp }(F)$
de sorte que, pour tout tel élément
![]() $Y$
et pour toute
$Y$
et pour toute
![]() $\unicode[STIX]{x1D719}\in C_{c}^{\infty }(\mathfrak{g}_{\sharp }(F))$
, on ait l’égalité
$\unicode[STIX]{x1D719}\in C_{c}^{\infty }(\mathfrak{g}_{\sharp }(F))$
, on ait l’égalité
Les éléments
![]() $X^{\unicode[STIX]{x1D701}}(a,e,u)$
ci-dessus, tels que
$X^{\unicode[STIX]{x1D701}}(a,e,u)$
ci-dessus, tels que
![]() $\sharp (a,e,u)=\sharp$
, sont elliptiques réguliers dans
$\sharp (a,e,u)=\sharp$
, sont elliptiques réguliers dans
![]() $\mathfrak{g}_{\sharp }(F)$
. On note
$\mathfrak{g}_{\sharp }(F)$
. On note
![]() $\hat{i} _{\sharp }^{\unicode[STIX]{x1D701}}[a,e,u]$
la fonction
$\hat{i} _{\sharp }^{\unicode[STIX]{x1D701}}[a,e,u]$
la fonction
![]() $Y\mapsto \hat{i} _{\sharp }(X^{\unicode[STIX]{x1D701}}(a,e,u),Y)$
. On pose
$Y\mapsto \hat{i} _{\sharp }(X^{\unicode[STIX]{x1D701}}(a,e,u),Y)$
. On pose
Pour un triplet
![]() $(a,e,u)$
tel que
$(a,e,u)$
tel que
![]() $\sharp (a,e,u)\not =\sharp$
, on pose
$\sharp (a,e,u)\not =\sharp$
, on pose
![]() $\hat{i} _{\sharp }[a,e,u]=0$
.
$\hat{i} _{\sharp }[a,e,u]=0$
.
On fixe une décomposition
![]() $\{1,\ldots ,t\}=K^{\prime }\sqcup K^{\prime \prime }$
de sorte que
$\{1,\ldots ,t\}=K^{\prime }\sqcup K^{\prime \prime }$
de sorte que
![]() $\unicode[STIX]{x1D6FD}^{\prime }$
, respectivement
$\unicode[STIX]{x1D6FD}^{\prime }$
, respectivement
![]() $\unicode[STIX]{x1D6FD}^{\prime \prime }$
, soit formée des
$\unicode[STIX]{x1D6FD}^{\prime \prime }$
, soit formée des
![]() $\unicode[STIX]{x1D6FD}_{k}$
pour
$\unicode[STIX]{x1D6FD}_{k}$
pour
![]() $k\in K^{\prime }$
, respectivement
$k\in K^{\prime }$
, respectivement
![]() $k\in K^{\prime \prime }$
. On définit un caractère
$k\in K^{\prime \prime }$
. On définit un caractère
![]() $\unicode[STIX]{x1D705}^{{\mathcal{U}}}$
de
$\unicode[STIX]{x1D705}^{{\mathcal{U}}}$
de
![]() ${\mathcal{U}}$
par
${\mathcal{U}}$
par
On va se limiter à un sous-groupe
![]() ${\mathcal{E}}^{0}$
de
${\mathcal{E}}^{0}$
de
![]() ${\mathcal{E}}$
. C’est le sous-groupe des familles
${\mathcal{E}}$
. C’est le sous-groupe des familles
![]() $e=(e_{j})_{j\in J}\in {\mathcal{E}}$
telles que
$e=(e_{j})_{j\in J}\in {\mathcal{E}}$
telles que
pour tout
![]() $j\in {\hat{J}}$
, tel que
$j\in {\hat{J}}$
, tel que
![]() $j<R$
,
$j<R$
,
![]() $e_{j-1}=e_{j}$
.
$e_{j-1}=e_{j}$
.
Remarque.
La condition
![]() $j<R$
est automatique si
$j<R$
est automatique si
![]() $r>0$
.
$r>0$
.
On définit le caractère
![]() $\unicode[STIX]{x1D705}^{0}$
du groupe
$\unicode[STIX]{x1D705}^{0}$
du groupe
![]() ${\mathcal{E}}^{0}$
par
${\mathcal{E}}^{0}$
par
On doit enfin définir quelques constantes. On note
![]() ${\mathcal{O}}(w^{\prime })$
et
${\mathcal{O}}(w^{\prime })$
et
![]() ${\mathcal{O}}(w^{\prime \prime })$
les classes de conjugaison de
${\mathcal{O}}(w^{\prime \prime })$
les classes de conjugaison de
![]() $w^{\prime }$
dans
$w^{\prime }$
dans
![]() $W_{N^{\prime }}$
et de
$W_{N^{\prime }}$
et de
![]() $w^{\prime \prime }$
dans
$w^{\prime \prime }$
dans
![]() $W_{N^{\prime \prime }}$
. On pose
$W_{N^{\prime \prime }}$
. On pose
et on définit
![]() $C(w^{\prime \prime })$
de façon similaire. On pose
$C(w^{\prime \prime })$
de façon similaire. On pose
![]() $\unicode[STIX]{x1D6FC}(r^{\prime },r^{\prime \prime },w^{\prime },w^{\prime \prime })=\operatorname{sgn}((-1)^{(r^{\prime }+r^{\prime \prime })/2}\unicode[STIX]{x1D702}\unicode[STIX]{x1D71B}^{-\operatorname{val}_{F}(\unicode[STIX]{x1D702})})$
si
$\unicode[STIX]{x1D6FC}(r^{\prime },r^{\prime \prime },w^{\prime },w^{\prime \prime })=\operatorname{sgn}((-1)^{(r^{\prime }+r^{\prime \prime })/2}\unicode[STIX]{x1D702}\unicode[STIX]{x1D71B}^{-\operatorname{val}_{F}(\unicode[STIX]{x1D702})})$
si
![]() $\operatorname{val}_{F}(\unicode[STIX]{x1D702})$
est pair ;
$\operatorname{val}_{F}(\unicode[STIX]{x1D702})$
est pair ;
![]() $\unicode[STIX]{x1D6FC}(r^{\prime },r^{\prime \prime },w^{\prime },w^{\prime \prime })=\operatorname{sgn}((-1)^{(r^{\prime }+r^{\prime \prime })/2}\unicode[STIX]{x1D702}\unicode[STIX]{x1D71B}^{-\operatorname{val}_{F}(\unicode[STIX]{x1D702})})\operatorname{sgn}_{CD}(w^{\prime })\operatorname{sgn}_{CD}(w^{\prime \prime })$
si
$\unicode[STIX]{x1D6FC}(r^{\prime },r^{\prime \prime },w^{\prime },w^{\prime \prime })=\operatorname{sgn}((-1)^{(r^{\prime }+r^{\prime \prime })/2}\unicode[STIX]{x1D702}\unicode[STIX]{x1D71B}^{-\operatorname{val}_{F}(\unicode[STIX]{x1D702})})\operatorname{sgn}_{CD}(w^{\prime })\operatorname{sgn}_{CD}(w^{\prime \prime })$
si
![]() $\operatorname{val}_{F}(\unicode[STIX]{x1D702})$
est impair ;
$\operatorname{val}_{F}(\unicode[STIX]{x1D702})$
est impair ;
Lemme. Pour
![]() $\sharp =\operatorname{iso}$
ou
$\sharp =\operatorname{iso}$
ou
![]() $\operatorname{an}$
et pour tout élément
$\operatorname{an}$
et pour tout élément
![]() $Y\in \mathfrak{g}_{\sharp }(F)$
qui est elliptique, régulier et topologiquement nilpotent, on a l’égalité
$Y\in \mathfrak{g}_{\sharp }(F)$
qui est elliptique, régulier et topologiquement nilpotent, on a l’égalité
 $$\begin{eqnarray}\displaystyle J(Y,f_{\sharp }) & = & \displaystyle C(w^{\prime })C(w^{\prime \prime })C(r^{\prime },r^{\prime \prime })\unicode[STIX]{x1D6FC}(r^{\prime },r^{\prime \prime },w^{\prime },w^{\prime \prime })\mathop{\sum }_{\unicode[STIX]{x1D6FE}\in \unicode[STIX]{x1D6E4}}\unicode[STIX]{x1D70E}(\unicode[STIX]{x1D6FE})\nonumber\\ \displaystyle & & \displaystyle \times \,\int _{A(\unicode[STIX]{x1D6FE})}\mathop{\sum }_{e\in {\mathcal{E}}^{0}}\mathop{\sum }_{u\in {\mathcal{U}}}\unicode[STIX]{x1D705}^{0}(e)\unicode[STIX]{x1D705}^{{\mathcal{U}}}(u)\hat{i} _{\sharp }[a,e,u](Y)\,da.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle J(Y,f_{\sharp }) & = & \displaystyle C(w^{\prime })C(w^{\prime \prime })C(r^{\prime },r^{\prime \prime })\unicode[STIX]{x1D6FC}(r^{\prime },r^{\prime \prime },w^{\prime },w^{\prime \prime })\mathop{\sum }_{\unicode[STIX]{x1D6FE}\in \unicode[STIX]{x1D6E4}}\unicode[STIX]{x1D70E}(\unicode[STIX]{x1D6FE})\nonumber\\ \displaystyle & & \displaystyle \times \,\int _{A(\unicode[STIX]{x1D6FE})}\mathop{\sum }_{e\in {\mathcal{E}}^{0}}\mathop{\sum }_{u\in {\mathcal{U}}}\unicode[STIX]{x1D705}^{0}(e)\unicode[STIX]{x1D705}^{{\mathcal{U}}}(u)\hat{i} _{\sharp }[a,e,u](Y)\,da.\nonumber\end{eqnarray}$$
Preuve.
Posons
![]() $N=N^{\prime }+N^{\prime \prime }$
. En [Reference Moeglin and Waldspurger6] 3.15 (1), on a écrit une égalité
$N=N^{\prime }+N^{\prime \prime }$
. En [Reference Moeglin and Waldspurger6] 3.15 (1), on a écrit une égalité
Les
![]() ${\mathcal{Q}}(r^{\prime },r^{\prime \prime };v^{\prime },v^{\prime \prime })_{\sharp }^{\operatorname{Lie}}$
sont des fonctions sur
${\mathcal{Q}}(r^{\prime },r^{\prime \prime };v^{\prime },v^{\prime \prime })_{\sharp }^{\operatorname{Lie}}$
sont des fonctions sur
![]() $\mathfrak{g}_{\sharp }(F)$
et les
$\mathfrak{g}_{\sharp }(F)$
et les
![]() $b(v^{\prime },v^{\prime \prime })$
sont des coefficients. L’ensemble
$b(v^{\prime },v^{\prime \prime })$
sont des coefficients. L’ensemble
![]() ${\mathcal{V}}_{n^{\prime },n^{\prime \prime },\sharp }$
est un ensemble de représentants des classes de conjugaison dans
${\mathcal{V}}_{n^{\prime },n^{\prime \prime },\sharp }$
est un ensemble de représentants des classes de conjugaison dans
![]() $W_{n^{\prime }}\times W_{n^{\prime \prime }}$
paramétrées par des couples de partitions de la forme
$W_{n^{\prime }}\times W_{n^{\prime \prime }}$
paramétrées par des couples de partitions de la forme
![]() $(\emptyset ,\unicode[STIX]{x1D6FF}^{\prime })$
,
$(\emptyset ,\unicode[STIX]{x1D6FF}^{\prime })$
,
![]() $(\emptyset ,\unicode[STIX]{x1D6FF}^{\prime \prime })$
et tels que
$(\emptyset ,\unicode[STIX]{x1D6FF}^{\prime \prime })$
et tels que
![]() $\unicode[STIX]{x1D6FF}^{\prime }\cup \unicode[STIX]{x1D6FF}^{\prime \prime }=\unicode[STIX]{x1D6FD}$
. Il y a une restriction (l’hypothèse 3.13(1) de [Reference Moeglin and Waldspurger6]), que nous levons en posant
$\unicode[STIX]{x1D6FF}^{\prime }\cup \unicode[STIX]{x1D6FF}^{\prime \prime }=\unicode[STIX]{x1D6FD}$
. Il y a une restriction (l’hypothèse 3.13(1) de [Reference Moeglin and Waldspurger6]), que nous levons en posant
![]() ${\mathcal{Q}}(r^{\prime },r^{\prime \prime };v^{\prime },v^{\prime \prime })_{\sharp }^{\operatorname{Lie}}=0$
si elle n’est pas vérifiée (dans [Reference Moeglin and Waldspurger6], cette fonction n’est définie que sous cette hypothèse 3.13(1)). En supprimant ainsi cette restriction, l’ensemble
${\mathcal{Q}}(r^{\prime },r^{\prime \prime };v^{\prime },v^{\prime \prime })_{\sharp }^{\operatorname{Lie}}=0$
si elle n’est pas vérifiée (dans [Reference Moeglin and Waldspurger6], cette fonction n’est définie que sous cette hypothèse 3.13(1)). En supprimant ainsi cette restriction, l’ensemble
![]() ${\mathcal{V}}_{n^{\prime },n^{\prime \prime },\sharp }$
devient indépendant de l’indice
${\mathcal{V}}_{n^{\prime },n^{\prime \prime },\sharp }$
devient indépendant de l’indice
![]() $\sharp$
et nous supprimons cet indice. Il y a une application naturelle
$\sharp$
et nous supprimons cet indice. Il y a une application naturelle
Pour
![]() $u=(u_{k})_{k=1,\ldots ,t}\in {\mathcal{U}}$
, on note
$u=(u_{k})_{k=1,\ldots ,t}\in {\mathcal{U}}$
, on note
![]() $\unicode[STIX]{x1D6FF}^{\prime }(u)$
la partition formée des
$\unicode[STIX]{x1D6FF}^{\prime }(u)$
la partition formée des
![]() $\unicode[STIX]{x1D6FD}_{k}$
pour
$\unicode[STIX]{x1D6FD}_{k}$
pour
![]() $k$
tel que
$k$
tel que
![]() $u_{k}=0$
et
$u_{k}=0$
et
![]() $\unicode[STIX]{x1D6FF}^{\prime \prime }(u)$
celle formée des
$\unicode[STIX]{x1D6FF}^{\prime \prime }(u)$
celle formée des
![]() $\unicode[STIX]{x1D6FD}_{k}$
pour
$\unicode[STIX]{x1D6FD}_{k}$
pour
![]() $k$
tel que
$k$
tel que
![]() $u(k)=1$
. L’application ci-dessus envoie
$u(k)=1$
. L’application ci-dessus envoie
![]() $u$
sur le couple de classes de conjugaison paramétrées par
$u$
sur le couple de classes de conjugaison paramétrées par
![]() $(\emptyset ,\unicode[STIX]{x1D6FF}^{\prime }(u))$
et
$(\emptyset ,\unicode[STIX]{x1D6FF}^{\prime }(u))$
et
![]() $(\emptyset ,\unicode[STIX]{x1D6FF}^{\prime \prime }(u))$
. L’égalité 3.15(6) de [Reference Moeglin and Waldspurger6] et les calculs qui la suivent montrent que, pour
$(\emptyset ,\unicode[STIX]{x1D6FF}^{\prime \prime }(u))$
. L’égalité 3.15(6) de [Reference Moeglin and Waldspurger6] et les calculs qui la suivent montrent que, pour
![]() $(v^{\prime },v^{\prime \prime })\in \cup _{(n^{\prime },n^{\prime \prime })\in D(N)}{\mathcal{V}}_{n^{\prime },n^{\prime \prime }}$
, on a l’égalité
$(v^{\prime },v^{\prime \prime })\in \cup _{(n^{\prime },n^{\prime \prime })\in D(N)}{\mathcal{V}}_{n^{\prime },n^{\prime \prime }}$
, on a l’égalité
où
Fixons
![]() $(v^{\prime },v^{\prime \prime })\in \bigcup _{(n^{\prime },n^{\prime \prime })\in D(N)}{\mathcal{V}}_{n^{\prime },n^{\prime \prime }}$
. L’intégrale orbitale
$(v^{\prime },v^{\prime \prime })\in \bigcup _{(n^{\prime },n^{\prime \prime })\in D(N)}{\mathcal{V}}_{n^{\prime },n^{\prime \prime }}$
. L’intégrale orbitale
![]() $J(Y,{\mathcal{Q}}(r^{\prime },r^{\prime \prime };v^{\prime },v^{\prime \prime })_{\sharp }^{\operatorname{Lie}})$
est calculée par une application successive des propositions 3.13 et 3.14 de [Reference Moeglin and Waldspurger6], où l’on remplace
$J(Y,{\mathcal{Q}}(r^{\prime },r^{\prime \prime };v^{\prime },v^{\prime \prime })_{\sharp }^{\operatorname{Lie}})$
est calculée par une application successive des propositions 3.13 et 3.14 de [Reference Moeglin and Waldspurger6], où l’on remplace
![]() $(w^{\prime },w^{\prime \prime })$
par
$(w^{\prime },w^{\prime \prime })$
par
![]() $(v^{\prime },v^{\prime \prime })$
. On obtient
$(v^{\prime },v^{\prime \prime })$
. On obtient
 $$\begin{eqnarray}\displaystyle & & \displaystyle J(Y,{\mathcal{Q}}(r^{\prime },r^{\prime \prime };v^{\prime },v^{\prime \prime })_{\sharp }^{\operatorname{Lie}})\nonumber\\ \displaystyle & & \displaystyle \quad =C_{2}(r^{\prime },r^{\prime \prime },v^{\prime },v^{\prime \prime })\mathop{\sum }_{\unicode[STIX]{x1D6FE}\in \unicode[STIX]{x1D6E4}}\unicode[STIX]{x1D70E}(\unicode[STIX]{x1D6FE})\nonumber\\ \displaystyle & & \displaystyle \qquad \times \,\int _{A(\unicode[STIX]{x1D6FE})}\mathop{\sum }_{e\in {\mathcal{E}}_{MW}^{0}}\unicode[STIX]{x1D705}_{MW}^{0}(e)\hat{i} _{\sharp ,MW}[a,e,v^{\prime },v^{\prime \prime }](Y)\,da,\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle J(Y,{\mathcal{Q}}(r^{\prime },r^{\prime \prime };v^{\prime },v^{\prime \prime })_{\sharp }^{\operatorname{Lie}})\nonumber\\ \displaystyle & & \displaystyle \quad =C_{2}(r^{\prime },r^{\prime \prime },v^{\prime },v^{\prime \prime })\mathop{\sum }_{\unicode[STIX]{x1D6FE}\in \unicode[STIX]{x1D6E4}}\unicode[STIX]{x1D70E}(\unicode[STIX]{x1D6FE})\nonumber\\ \displaystyle & & \displaystyle \qquad \times \,\int _{A(\unicode[STIX]{x1D6FE})}\mathop{\sum }_{e\in {\mathcal{E}}_{MW}^{0}}\unicode[STIX]{x1D705}_{MW}^{0}(e)\hat{i} _{\sharp ,MW}[a,e,v^{\prime },v^{\prime \prime }](Y)\,da,\end{eqnarray}$$
où
![]() $C_{2}(r^{\prime },r^{\prime \prime },v^{\prime },v^{\prime \prime })$
est une certaine constante sur laquelle nous allons revenir ;
$C_{2}(r^{\prime },r^{\prime \prime },v^{\prime },v^{\prime \prime })$
est une certaine constante sur laquelle nous allons revenir ;
![]() $\unicode[STIX]{x1D6E4}$
et, pour
$\unicode[STIX]{x1D6E4}$
et, pour
![]() $\unicode[STIX]{x1D6FE}\in \unicode[STIX]{x1D6E4}$
,
$\unicode[STIX]{x1D6FE}\in \unicode[STIX]{x1D6E4}$
,
![]() $A(\unicode[STIX]{x1D6FE})$
et
$A(\unicode[STIX]{x1D6FE})$
et
![]() $\unicode[STIX]{x1D70E}(\unicode[STIX]{x1D6FE})$
sont les termes que l’on a définis ci-dessus ;
$\unicode[STIX]{x1D70E}(\unicode[STIX]{x1D6FE})$
sont les termes que l’on a définis ci-dessus ;
les autres termes
![]() ${\mathcal{E}}_{MW}^{0}$
, etc., sont quelque peu différents des nôtres, on y a ajouté un indice
${\mathcal{E}}_{MW}^{0}$
, etc., sont quelque peu différents des nôtres, on y a ajouté un indice
![]() $MW$
pour les en distinguer.
$MW$
pour les en distinguer.
On constate que le couple
![]() $(v^{\prime },v^{\prime \prime })$
intervient dans (5) d’une part par la constante, d’autre part par la fonction
$(v^{\prime },v^{\prime \prime })$
intervient dans (5) d’une part par la constante, d’autre part par la fonction
![]() $\hat{i} _{\sharp ,MW}[a,e,v^{\prime },v^{\prime \prime }]$
. Pour ce qui est de la constante, le couple
$\hat{i} _{\sharp ,MW}[a,e,v^{\prime },v^{\prime \prime }]$
. Pour ce qui est de la constante, le couple
![]() $(v^{\prime },v^{\prime \prime })$
intervient via des termes
$(v^{\prime },v^{\prime \prime })$
intervient via des termes
![]() $|T^{\prime }||T^{\prime \prime }|$
et des produits
$|T^{\prime }||T^{\prime \prime }|$
et des produits
![]() $\operatorname{sgn}_{CD}(v^{\prime })\operatorname{sgn}_{CD}(v^{\prime \prime })$
, cf. les formules de [Reference Moeglin and Waldspurger6]. Il résulte de la définition ci-dessus que ce dernier produit vaut
$\operatorname{sgn}_{CD}(v^{\prime })\operatorname{sgn}_{CD}(v^{\prime \prime })$
, cf. les formules de [Reference Moeglin and Waldspurger6]. Il résulte de la définition ci-dessus que ce dernier produit vaut
![]() $\operatorname{sgn}_{CD}(w^{\prime })\operatorname{sgn}_{CD}(w^{\prime \prime })$
. En se reportant à la définition des tores
$\operatorname{sgn}_{CD}(w^{\prime })\operatorname{sgn}_{CD}(w^{\prime \prime })$
. En se reportant à la définition des tores
![]() $T^{\prime }$
et
$T^{\prime }$
et
![]() $T^{\prime \prime }$
, on calcule explicitement
$T^{\prime \prime }$
, on calcule explicitement
En conclusion,
![]() $C_{2}(r^{\prime },r^{\prime \prime },v^{\prime },v^{\prime \prime })$
ne dépend pas de
$C_{2}(r^{\prime },r^{\prime \prime },v^{\prime },v^{\prime \prime })$
ne dépend pas de
![]() $(v^{\prime },v^{\prime \prime })$
mais seulement de
$(v^{\prime },v^{\prime \prime })$
mais seulement de
![]() $(w^{\prime },w^{\prime \prime })$
. On la note plutôt
$(w^{\prime },w^{\prime \prime })$
. On la note plutôt
![]() $C_{2}(r^{\prime },r^{\prime \prime },w^{\prime },w^{\prime \prime })$
. Quant à la fonction
$C_{2}(r^{\prime },r^{\prime \prime },w^{\prime },w^{\prime \prime })$
. Quant à la fonction
![]() $\hat{i} _{\sharp ,MW}[a,e,v^{\prime },v^{\prime \prime }]$
, elle ne dépend de
$\hat{i} _{\sharp ,MW}[a,e,v^{\prime },v^{\prime \prime }]$
, elle ne dépend de
![]() $(v^{\prime },v^{\prime \prime })$
que par un élément
$(v^{\prime },v^{\prime \prime })$
que par un élément
![]() $X$
défini en [Reference Moeglin and Waldspurger6] 3.13. On a un certain choix pour cet élément. On constate que, pour tout
$X$
défini en [Reference Moeglin and Waldspurger6] 3.13. On a un certain choix pour cet élément. On constate que, pour tout
![]() $u\in \unicode[STIX]{x1D6FF}^{-1}(v^{\prime },v^{\prime \prime })$
, on peut prendre pour
$u\in \unicode[STIX]{x1D6FF}^{-1}(v^{\prime },v^{\prime \prime })$
, on peut prendre pour
![]() $X$
un élément construit comme ci-dessus à l’aide des données
$X$
un élément construit comme ci-dessus à l’aide des données
![]() $(X_{k})_{k=1,\ldots ,t}$
et
$(X_{k})_{k=1,\ldots ,t}$
et
![]() $u$
. Notons
$u$
. Notons
![]() $\hat{i} _{\sharp ,MW}[a,e,u]$
la fonction associée à ce choix. L’égalité suivante résulte alors de (2), (3) et (5) :
$\hat{i} _{\sharp ,MW}[a,e,u]$
la fonction associée à ce choix. L’égalité suivante résulte alors de (2), (3) et (5) :
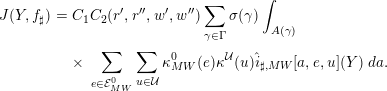 $$\begin{eqnarray}\displaystyle J(Y,f_{\sharp }) & = & \displaystyle C_{1}C_{2}(r^{\prime },r^{\prime \prime },w^{\prime },w^{\prime \prime })\mathop{\sum }_{\unicode[STIX]{x1D6FE}\in \unicode[STIX]{x1D6E4}}\unicode[STIX]{x1D70E}(\unicode[STIX]{x1D6FE})\int _{A(\unicode[STIX]{x1D6FE})}\nonumber\\ \displaystyle & & \displaystyle \times \,\mathop{\sum }_{e\in {\mathcal{E}}_{MW}^{0}}\mathop{\sum }_{u\in {\mathcal{U}}}\unicode[STIX]{x1D705}_{MW}^{0}(e)\unicode[STIX]{x1D705}^{{\mathcal{U}}}(u)\hat{i} _{\sharp ,MW}[a,e,u](Y)\,da.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle J(Y,f_{\sharp }) & = & \displaystyle C_{1}C_{2}(r^{\prime },r^{\prime \prime },w^{\prime },w^{\prime \prime })\mathop{\sum }_{\unicode[STIX]{x1D6FE}\in \unicode[STIX]{x1D6E4}}\unicode[STIX]{x1D70E}(\unicode[STIX]{x1D6FE})\int _{A(\unicode[STIX]{x1D6FE})}\nonumber\\ \displaystyle & & \displaystyle \times \,\mathop{\sum }_{e\in {\mathcal{E}}_{MW}^{0}}\mathop{\sum }_{u\in {\mathcal{U}}}\unicode[STIX]{x1D705}_{MW}^{0}(e)\unicode[STIX]{x1D705}^{{\mathcal{U}}}(u)\hat{i} _{\sharp ,MW}[a,e,u](Y)\,da.\end{eqnarray}$$
Supposons que
![]() $(r^{\prime },r^{\prime \prime })\not =(0,0)$
. Il y a une application naturelle de notre ensemble
$(r^{\prime },r^{\prime \prime })\not =(0,0)$
. Il y a une application naturelle de notre ensemble
![]() ${\mathcal{E}}^{0}$
dans l’ensemble
${\mathcal{E}}^{0}$
dans l’ensemble
![]() ${\mathcal{E}}_{MW}^{0}$
. À
${\mathcal{E}}_{MW}^{0}$
. À
![]() $e\in {\mathcal{E}}^{0}$
, elle associe l’unique élément
$e\in {\mathcal{E}}^{0}$
, elle associe l’unique élément
![]() $e_{MW}\in {\mathcal{E}}_{MW}^{0}$
tel que
$e_{MW}\in {\mathcal{E}}_{MW}^{0}$
tel que
![]() $e_{MW,j}=e_{j}$
pour
$e_{MW,j}=e_{j}$
pour
![]() $j=1,\ldots ,R-1$
. L’élément
$j=1,\ldots ,R-1$
. L’élément
![]() $e_{MW,R}$
est défini par les égalités
$e_{MW,R}$
est défini par les égalités
![]() $\prod _{j=R-r+1,\ldots ,R}e_{MW,j}=1$
si
$\prod _{j=R-r+1,\ldots ,R}e_{MW,j}=1$
si
![]() $r>0$
;
$r>0$
;
![]() $e_{MW,R}=e_{MW,R-1}$
si
$e_{MW,R}=e_{MW,R-1}$
si
![]() $r=0$
.
$r=0$
.
On constate que
![]() $\unicode[STIX]{x1D705}^{0}(e)=\unicode[STIX]{x1D705}_{MW}^{0}(e_{MW})$
. Fixons
$\unicode[STIX]{x1D705}^{0}(e)=\unicode[STIX]{x1D705}_{MW}^{0}(e_{MW})$
. Fixons
![]() $\unicode[STIX]{x1D6FE}\in \unicode[STIX]{x1D6E4}$
et
$\unicode[STIX]{x1D6FE}\in \unicode[STIX]{x1D6E4}$
et
![]() $a\in A(\unicode[STIX]{x1D6FE})$
. Dans l’énoncé du lemme, on peut évidemment limiter la somme en
$a\in A(\unicode[STIX]{x1D6FE})$
. Dans l’énoncé du lemme, on peut évidemment limiter la somme en
![]() $e$
et
$e$
et
![]() $u$
à la somme sur les couples
$u$
à la somme sur les couples
![]() $(e,u)$
tels que
$(e,u)$
tels que
![]() $\sharp (a,e,u)=\sharp$
: si cette condition n’est pas vérifiée,
$\sharp (a,e,u)=\sharp$
: si cette condition n’est pas vérifiée,
![]() $\hat{i} _{\sharp }[a,e,u]=0$
. Notons
$\hat{i} _{\sharp }[a,e,u]=0$
. Notons
![]() $({\mathcal{E}}^{0}\times {\mathcal{U}})_{a,\sharp }$
ce sous-ensemble. On constate alors que l’application
$({\mathcal{E}}^{0}\times {\mathcal{U}})_{a,\sharp }$
ce sous-ensemble. On constate alors que l’application
est bijective et que, pour
![]() $(e,u)\in ({\mathcal{E}}^{0}\times {\mathcal{U}})_{a,\sharp }$
, on a l’égalité
$(e,u)\in ({\mathcal{E}}^{0}\times {\mathcal{U}})_{a,\sharp }$
, on a l’égalité
![]() $\hat{i} _{\sharp ,MW}[a,e_{MW},u]=\hat{i} _{\sharp }[a,e,u]$
. En utilisant ces propriétés, l’égalité (7) devient alors l’égalité de l’énoncé, aux constantes près. Il ne reste donc plus qu’à démontrer l’égalité
$\hat{i} _{\sharp ,MW}[a,e_{MW},u]=\hat{i} _{\sharp }[a,e,u]$
. En utilisant ces propriétés, l’égalité (7) devient alors l’égalité de l’énoncé, aux constantes près. Il ne reste donc plus qu’à démontrer l’égalité
On a supposé que
![]() $(r^{\prime },r^{\prime \prime })\not =(0,0)$
. Si
$(r^{\prime },r^{\prime \prime })\not =(0,0)$
. Si
![]() $(r^{\prime },r^{\prime \prime })=(0,0)$
, les termes
$(r^{\prime },r^{\prime \prime })=(0,0)$
, les termes
![]() $\unicode[STIX]{x1D6E4}$
,
$\unicode[STIX]{x1D6E4}$
,
![]() ${\mathcal{E}}^{0}$
, etc., disparaissent et la formule (7) se compare directement à celle de l’énoncé. De nouveau, il ne reste plus qu’à comparer les constantes.
${\mathcal{E}}^{0}$
, etc., disparaissent et la formule (7) se compare directement à celle de l’énoncé. De nouveau, il ne reste plus qu’à comparer les constantes.
La constante
![]() $C_{2}(r^{\prime },r^{\prime \prime },w^{\prime },w^{\prime \prime })$
est le produit de la constante
$C_{2}(r^{\prime },r^{\prime \prime },w^{\prime },w^{\prime \prime })$
est le produit de la constante
![]() $C\unicode[STIX]{x1D6FC}(w^{\prime },w^{\prime \prime })_{\sharp }$
de la proposition 3.14 de [Reference Moeglin and Waldspurger6] et de l’inverse de la constante de la proposition 3.13 de cette référence. Malheureusement, il y a des erreurs dans ces constantes. On a déjà effectué quelques corrections dans [Reference Waldspurger8] page 335 :
$C\unicode[STIX]{x1D6FC}(w^{\prime },w^{\prime \prime })_{\sharp }$
de la proposition 3.14 de [Reference Moeglin and Waldspurger6] et de l’inverse de la constante de la proposition 3.13 de cette référence. Malheureusement, il y a des erreurs dans ces constantes. On a déjà effectué quelques corrections dans [Reference Waldspurger8] page 335 :
la constante de la proposition 3.13 est
(en réalité,
![]() $T^{\prime }$
et
$T^{\prime }$
et
![]() $T^{\prime \prime }$
sont associés à un couple
$T^{\prime \prime }$
sont associés à un couple
![]() $(v^{\prime },v^{\prime \prime })\in {\mathcal{V}}_{n^{\prime },n^{\prime \prime }}$
mais, d’après (5), le produit de leurs nombres d’éléments en est indépendant) ;
$(v^{\prime },v^{\prime \prime })\in {\mathcal{V}}_{n^{\prime },n^{\prime \prime }}$
mais, d’après (5), le produit de leurs nombres d’éléments en est indépendant) ;
on a l’égalité
A l’aide de (4) et (6), on voit que le produit de
![]() $C_{1}$
,
$C_{1}$
,
![]() $C$
et de l’inverse de (9) vaut
$C$
et de l’inverse de (9) vaut
![]() $C(w^{\prime })C(w^{\prime \prime })C(r^{\prime },r^{\prime \prime })\unicode[STIX]{x1D6FE}(r^{\prime },r^{\prime \prime })_{\sharp }^{-1}$
. Rappelons qu’en [Reference Waldspurger11] 1.1, on a associé à
$C(w^{\prime })C(w^{\prime \prime })C(r^{\prime },r^{\prime \prime })\unicode[STIX]{x1D6FE}(r^{\prime },r^{\prime \prime })_{\sharp }^{-1}$
. Rappelons qu’en [Reference Waldspurger11] 1.1, on a associé à
![]() $Q_{\sharp }$
des discriminants
$Q_{\sharp }$
des discriminants
![]() $\unicode[STIX]{x1D702}^{\prime }(Q_{\sharp })$
et
$\unicode[STIX]{x1D702}^{\prime }(Q_{\sharp })$
et
![]() $\unicode[STIX]{x1D702}^{\prime \prime }(Q_{\sharp })$
, notons-les simplement
$\unicode[STIX]{x1D702}^{\prime \prime }(Q_{\sharp })$
, notons-les simplement
![]() $\unicode[STIX]{x1D702}_{\sharp }^{\prime }$
et
$\unicode[STIX]{x1D702}_{\sharp }^{\prime }$
et
![]() $\unicode[STIX]{x1D702}_{\sharp }^{\prime \prime }$
. D’après [Reference Moeglin and Waldspurger6] 3.13, on a
$\unicode[STIX]{x1D702}_{\sharp }^{\prime \prime }$
. D’après [Reference Moeglin and Waldspurger6] 3.13, on a
![]() $\unicode[STIX]{x1D6FE}(r^{\prime },r^{\prime \prime })_{\sharp }=\operatorname{sgn}((-1)^{(r^{\prime }+r^{\prime \prime })/2}\unicode[STIX]{x1D702}_{\sharp }^{\prime }\unicode[STIX]{x1D702}_{\sharp }^{\prime \prime })$
, si
$\unicode[STIX]{x1D6FE}(r^{\prime },r^{\prime \prime })_{\sharp }=\operatorname{sgn}((-1)^{(r^{\prime }+r^{\prime \prime })/2}\unicode[STIX]{x1D702}_{\sharp }^{\prime }\unicode[STIX]{x1D702}_{\sharp }^{\prime \prime })$
, si
![]() $r^{\prime }$
et
$r^{\prime }$
et
![]() $r^{\prime \prime }$
sont pairs, c’est-à-dire si
$r^{\prime \prime }$
sont pairs, c’est-à-dire si
![]() $\operatorname{val}_{F}(\unicode[STIX]{x1D702})$
est pair ;
$\operatorname{val}_{F}(\unicode[STIX]{x1D702})$
est pair ;
![]() $\unicode[STIX]{x1D6FE}(r^{\prime },r^{\prime \prime })_{\sharp }=1$
si
$\unicode[STIX]{x1D6FE}(r^{\prime },r^{\prime \prime })_{\sharp }=1$
si
![]() $\operatorname{val}_{F}(\unicode[STIX]{x1D702})$
est impair.
$\operatorname{val}_{F}(\unicode[STIX]{x1D702})$
est impair.
Il y a une autre correction à apporter à [Reference Moeglin and Waldspurger6]. On a
![]() $\unicode[STIX]{x1D6FC}(w^{\prime },w^{\prime \prime })_{\sharp }=1$
si
$\unicode[STIX]{x1D6FC}(w^{\prime },w^{\prime \prime })_{\sharp }=1$
si
![]() $\operatorname{val}_{F}(\unicode[STIX]{x1D702})$
est pair ;
$\operatorname{val}_{F}(\unicode[STIX]{x1D702})$
est pair ;
![]() $\unicode[STIX]{x1D6FC}(w^{\prime },w^{\prime \prime })_{\sharp }=\operatorname{sgn}((-1)^{(r^{\prime }-r^{\prime \prime })/2}\unicode[STIX]{x1D702}_{\sharp }^{\prime }\unicode[STIX]{x1D702}_{\sharp }^{\prime \prime })\operatorname{sgn}_{CD}(w^{\prime })\operatorname{sgn}_{CD}(w^{\prime \prime })$
si
$\unicode[STIX]{x1D6FC}(w^{\prime },w^{\prime \prime })_{\sharp }=\operatorname{sgn}((-1)^{(r^{\prime }-r^{\prime \prime })/2}\unicode[STIX]{x1D702}_{\sharp }^{\prime }\unicode[STIX]{x1D702}_{\sharp }^{\prime \prime })\operatorname{sgn}_{CD}(w^{\prime })\operatorname{sgn}_{CD}(w^{\prime \prime })$
si
![]() $\operatorname{val}_{F}(\unicode[STIX]{x1D702})$
est impair.
$\operatorname{val}_{F}(\unicode[STIX]{x1D702})$
est impair.
Cette constante provient en fait de [Reference Waldspurger9] paragraphes VII.25 et VII.26. Dans cette référence, on avait supposé
![]() $r^{\prime }$
et
$r^{\prime }$
et
![]() $r^{\prime \prime }$
pairs et obtenu la constante
$r^{\prime \prime }$
pairs et obtenu la constante
![]() $1$
. Dans [Reference Moeglin and Waldspurger6], on a abusivement adopté cette valeur même quand
$1$
. Dans [Reference Moeglin and Waldspurger6], on a abusivement adopté cette valeur même quand
![]() $r^{\prime }$
et
$r^{\prime }$
et
![]() $r^{\prime \prime }$
sont impairs. En reprenant la preuve de [Reference Waldspurger9] VII.26 et en y supposant
$r^{\prime \prime }$
sont impairs. En reprenant la preuve de [Reference Waldspurger9] VII.26 et en y supposant
![]() $r^{\prime }$
et
$r^{\prime }$
et
![]() $r^{\prime \prime }$
impairs, on obtient la constante ci-dessus. Signalons que, dans le cas spécial orthogonal impair, il n’y a (à notre connaissance) pas de correction à apporter à la formule de [Reference Moeglin and Waldspurger6] pour la constante
$r^{\prime \prime }$
impairs, on obtient la constante ci-dessus. Signalons que, dans le cas spécial orthogonal impair, il n’y a (à notre connaissance) pas de correction à apporter à la formule de [Reference Moeglin and Waldspurger6] pour la constante
![]() $\unicode[STIX]{x1D6FC}(w^{\prime },w^{\prime \prime })_{\sharp }$
.
$\unicode[STIX]{x1D6FC}(w^{\prime },w^{\prime \prime })_{\sharp }$
.
D’après [Reference Waldspurger11] 1.1, on a l’égalité
![]() $\unicode[STIX]{x1D702}_{\sharp }^{\prime }\unicode[STIX]{x1D702}_{\sharp }^{\prime \prime }(-1)^{r^{\prime \prime }}=\unicode[STIX]{x1D702}\unicode[STIX]{x1D71B}^{-\operatorname{val}_{F}(\unicode[STIX]{x1D702})}$
. En la reportant dans la formule ci-dessus, on obtient l’égalité
$\unicode[STIX]{x1D702}_{\sharp }^{\prime }\unicode[STIX]{x1D702}_{\sharp }^{\prime \prime }(-1)^{r^{\prime \prime }}=\unicode[STIX]{x1D702}\unicode[STIX]{x1D71B}^{-\operatorname{val}_{F}(\unicode[STIX]{x1D702})}$
. En la reportant dans la formule ci-dessus, on obtient l’égalité
En mettant ces calculs bout à bout, on obtient l’égalité (8), ce qui achève la démonstration. ◻
2.5 Transformation de l’expression précédente
On note
![]() ${\mathcal{L}}$
l’ensemble des couples
${\mathcal{L}}$
l’ensemble des couples
![]() $(L_{1},L_{2})$
de sous-ensembles de
$(L_{1},L_{2})$
de sous-ensembles de
![]() $\{1,\ldots ,R-r\}$
tels que
$\{1,\ldots ,R-r\}$
tels que
![]() $\{1,\ldots ,R-r\}$
est la réunion disjointe de
$\{1,\ldots ,R-r\}$
est la réunion disjointe de
![]() $L_{1}$
et
$L_{1}$
et
![]() $L_{2}$
;
$L_{2}$
;
pour tout
![]() $j\in {\hat{J}}$
, les intersections
$j\in {\hat{J}}$
, les intersections
![]() $L_{1}\cap \{j-1,j\}$
et
$L_{1}\cap \{j-1,j\}$
et
![]() $L_{2}\cap \{j-1,j\}$
ont un unique élément ; on note cet élément
$L_{2}\cap \{j-1,j\}$
ont un unique élément ; on note cet élément
![]() $l_{1}(j/2)$
, respectivement
$l_{1}(j/2)$
, respectivement
![]() $l_{2}(j/2)$
;
$l_{2}(j/2)$
;
si
![]() $r=0$
et
$r=0$
et
![]() $R>0$
,
$R>0$
,
![]() $l_{2}(R/2)=R-1$
.
$l_{2}(R/2)=R-1$
.
Pour un tel couple, on définit un caractère
![]() $\unicode[STIX]{x1D705}^{L_{2}}$
de
$\unicode[STIX]{x1D705}^{L_{2}}$
de
![]() ${\mathcal{E}}$
par
${\mathcal{E}}$
par
Lemme. Pour
![]() $\sharp =\operatorname{iso}$
ou
$\sharp =\operatorname{iso}$
ou
![]() $\operatorname{an}$
et pour tout élément
$\operatorname{an}$
et pour tout élément
![]() $Y\in \mathfrak{g}_{\sharp }(F)$
qui est elliptique, régulier et topologiquement nilpotent, on a l’égalité
$Y\in \mathfrak{g}_{\sharp }(F)$
qui est elliptique, régulier et topologiquement nilpotent, on a l’égalité
 $$\begin{eqnarray}\displaystyle J(Y,f_{\sharp }) & = & \displaystyle C(w^{\prime })C(w^{\prime \prime })C(r^{\prime },r^{\prime \prime })\unicode[STIX]{x1D6FC}(r^{\prime },r^{\prime \prime },w^{\prime },w^{\prime \prime })|{\mathcal{L}}|^{-1}\mathop{\sum }_{(L_{1},L_{2})\in {\mathcal{L}}}\mathop{\sum }_{\unicode[STIX]{x1D6FE}\in \unicode[STIX]{x1D6E4}}\unicode[STIX]{x1D70E}(\unicode[STIX]{x1D6FE})\nonumber\\ \displaystyle & & \displaystyle \times \,\int _{A(\unicode[STIX]{x1D6FE})}\mathop{\sum }_{e\in {\mathcal{E}}}\mathop{\sum }_{u\in {\mathcal{U}}}\unicode[STIX]{x1D705}^{L_{2}}(e)\unicode[STIX]{x1D705}^{{\mathcal{U}}}(u)\hat{i} _{\sharp }[a,e,u](Y)\,da.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle J(Y,f_{\sharp }) & = & \displaystyle C(w^{\prime })C(w^{\prime \prime })C(r^{\prime },r^{\prime \prime })\unicode[STIX]{x1D6FC}(r^{\prime },r^{\prime \prime },w^{\prime },w^{\prime \prime })|{\mathcal{L}}|^{-1}\mathop{\sum }_{(L_{1},L_{2})\in {\mathcal{L}}}\mathop{\sum }_{\unicode[STIX]{x1D6FE}\in \unicode[STIX]{x1D6E4}}\unicode[STIX]{x1D70E}(\unicode[STIX]{x1D6FE})\nonumber\\ \displaystyle & & \displaystyle \times \,\int _{A(\unicode[STIX]{x1D6FE})}\mathop{\sum }_{e\in {\mathcal{E}}}\mathop{\sum }_{u\in {\mathcal{U}}}\unicode[STIX]{x1D705}^{L_{2}}(e)\unicode[STIX]{x1D705}^{{\mathcal{U}}}(u)\hat{i} _{\sharp }[a,e,u](Y)\,da.\nonumber\end{eqnarray}$$
Preuve.
En vertu de l’énoncé précédent, il suffit de prouver que, pour
![]() $e\in {\mathcal{E}}$
, on a les égalités
$e\in {\mathcal{E}}$
, on a les égalités
(1)
 $\sum _{(L_{1},L_{2})\in {\mathcal{L}}}\unicode[STIX]{x1D705}^{L_{2}}(e)=0$
si
$\sum _{(L_{1},L_{2})\in {\mathcal{L}}}\unicode[STIX]{x1D705}^{L_{2}}(e)=0$
si
 $e\not \in {\mathcal{E}}^{0}$
;
$e\not \in {\mathcal{E}}^{0}$
;(2)
 $\sum _{(L_{1},L_{2})\in {\mathcal{L}}}\unicode[STIX]{x1D705}^{L_{2}}(e)=|{\mathcal{L}}|\unicode[STIX]{x1D705}^{0}(e)$
, si
$\sum _{(L_{1},L_{2})\in {\mathcal{L}}}\unicode[STIX]{x1D705}^{L_{2}}(e)=|{\mathcal{L}}|\unicode[STIX]{x1D705}^{0}(e)$
, si
 $e\in {\mathcal{E}}^{0}$
.
$e\in {\mathcal{E}}^{0}$
.
Supposons que
![]() $e\not \in {\mathcal{E}}^{0}$
. Alors il existe
$e\not \in {\mathcal{E}}^{0}$
. Alors il existe
![]() $j\in \{1,\ldots ,(R-r)/2\}$
, avec
$j\in \{1,\ldots ,(R-r)/2\}$
, avec
![]() $j<R/2$
si
$j<R/2$
si
![]() $r=0$
et
$r=0$
et
![]() $R>0$
, de sorte que
$R>0$
, de sorte que
![]() $e_{2j-1}\not =e_{2j}$
. On fixe un tel
$e_{2j-1}\not =e_{2j}$
. On fixe un tel
![]() $j$
. On regroupe les éléments de
$j$
. On regroupe les éléments de
![]() ${\mathcal{L}}$
en paires. Si
${\mathcal{L}}$
en paires. Si
![]() $(L_{1},L_{2})$
est un élément d’une paire, l’autre élément
$(L_{1},L_{2})$
est un élément d’une paire, l’autre élément
![]() $(L_{1}^{\prime },L_{2}^{\prime })$
est obtenu en échangeant
$(L_{1}^{\prime },L_{2}^{\prime })$
est obtenu en échangeant
![]() $l_{1}(j)$
et
$l_{1}(j)$
et
![]() $l_{2}(j)$
et en ne changeant pas les autres
$l_{2}(j)$
et en ne changeant pas les autres
![]() $l_{1}(h)$
,
$l_{1}(h)$
,
![]() $l_{2}(h)$
pour
$l_{2}(h)$
pour
![]() $h\not =j$
. On a alors
$h\not =j$
. On a alors
 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D705}^{L_{2}}(e) & = & \displaystyle \operatorname{sgn}(e_{l_{2}(j)})\displaystyle \mathop{\prod }_{h\not =j}\operatorname{sgn}(e_{l_{2}(h)}),\nonumber\\ \displaystyle \unicode[STIX]{x1D705}^{L_{2}^{\prime }}(e) & = & \displaystyle \operatorname{sgn}(e_{l_{1}(j)})\displaystyle \mathop{\prod }_{h\not =j}\operatorname{sgn}(e_{l_{2}(h)}).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D705}^{L_{2}}(e) & = & \displaystyle \operatorname{sgn}(e_{l_{2}(j)})\displaystyle \mathop{\prod }_{h\not =j}\operatorname{sgn}(e_{l_{2}(h)}),\nonumber\\ \displaystyle \unicode[STIX]{x1D705}^{L_{2}^{\prime }}(e) & = & \displaystyle \operatorname{sgn}(e_{l_{1}(j)})\displaystyle \mathop{\prod }_{h\not =j}\operatorname{sgn}(e_{l_{2}(h)}).\nonumber\end{eqnarray}$$
Puisque
![]() $e_{l_{2}(j)}\not =e_{l_{1}(j)}$
, la somme de ces termes est nulle, ce qui prouve (1).
$e_{l_{2}(j)}\not =e_{l_{1}(j)}$
, la somme de ces termes est nulle, ce qui prouve (1).
Supposons que
![]() $e\in {\mathcal{E}}^{0}$
. Pour tout
$e\in {\mathcal{E}}^{0}$
. Pour tout
![]() $j=1,\ldots ,(R-r)/2$
et tout
$j=1,\ldots ,(R-r)/2$
et tout
![]() $(L_{1},L_{2})\in {\mathcal{L}}$
, on a l’égalité
$(L_{1},L_{2})\in {\mathcal{L}}$
, on a l’égalité
![]() $\operatorname{sgn}(e_{l_{2}(j)})=\operatorname{sgn}(e_{2j-1})$
. Cela résulte de l’égalité
$\operatorname{sgn}(e_{l_{2}(j)})=\operatorname{sgn}(e_{2j-1})$
. Cela résulte de l’égalité
![]() $e_{2j-1}=e_{2j}$
imposée aux éléments de
$e_{2j-1}=e_{2j}$
imposée aux éléments de
![]() ${\mathcal{E}}^{0}$
, sauf dans le cas où
${\mathcal{E}}^{0}$
, sauf dans le cas où
![]() $r=0$
,
$r=0$
,
![]() $R>0$
et
$R>0$
et
![]() $j=R/2$
. Mais dans ce cas,
$j=R/2$
. Mais dans ce cas,
![]() $l_{2}(j)=2j-1$
par définition de
$l_{2}(j)=2j-1$
par définition de
![]() ${\mathcal{L}}$
. En conséquence,
${\mathcal{L}}$
. En conséquence,
![]() $\unicode[STIX]{x1D705}^{L_{2}}(e)=\prod _{j=1,\ldots ,(R-r)/2}\operatorname{sgn}(e_{2j-1})=\unicode[STIX]{x1D705}^{0}(e)$
. D’où (2).◻
$\unicode[STIX]{x1D705}^{L_{2}}(e)=\prod _{j=1,\ldots ,(R-r)/2}\operatorname{sgn}(e_{2j-1})=\unicode[STIX]{x1D705}^{0}(e)$
. D’où (2).◻
2.6 Calcul de facteurs de transfert
Pour
![]() $\unicode[STIX]{x1D6FE}\in \unicode[STIX]{x1D6E4}$
,
$\unicode[STIX]{x1D6FE}\in \unicode[STIX]{x1D6E4}$
,
![]() $a\in A(\unicode[STIX]{x1D6FE})$
,
$a\in A(\unicode[STIX]{x1D6FE})$
,
![]() $e\in {\mathcal{E}}$
,
$e\in {\mathcal{E}}$
,
![]() $u\in {\mathcal{U}}$
et
$u\in {\mathcal{U}}$
et
![]() $\unicode[STIX]{x1D701}=\pm$
, on a introduit un élément
$\unicode[STIX]{x1D701}=\pm$
, on a introduit un élément
![]() $X^{\unicode[STIX]{x1D701}}(a,e,u)$
. Fixons
$X^{\unicode[STIX]{x1D701}}(a,e,u)$
. Fixons
![]() $\unicode[STIX]{x1D6FE}$
et
$\unicode[STIX]{x1D6FE}$
et
![]() $a$
. Quand
$a$
. Quand
![]() $e$
,
$e$
,
![]() $u$
et
$u$
et
![]() $\unicode[STIX]{x1D701}$
varient, ces éléments
$\unicode[STIX]{x1D701}$
varient, ces éléments
![]() $X^{\unicode[STIX]{x1D701}}(a,e,u)$
décrivent un ensemble de représentants des classes de conjugaison contenues dans deux classes totales de conjugaison stable dans
$X^{\unicode[STIX]{x1D701}}(a,e,u)$
décrivent un ensemble de représentants des classes de conjugaison contenues dans deux classes totales de conjugaison stable dans
![]() $\mathfrak{g}_{\operatorname{iso}}(F)\cup \mathfrak{g}_{\operatorname{an}}(F)$
. Ces deux classes se déduisent l’une de l’autre par conjugaison par des éléments de déterminant
$\mathfrak{g}_{\operatorname{iso}}(F)\cup \mathfrak{g}_{\operatorname{an}}(F)$
. Ces deux classes se déduisent l’une de l’autre par conjugaison par des éléments de déterminant
![]() $-1$
des groupes orthogonaux. On n’a pas donné de critère pour distinguer
$-1$
des groupes orthogonaux. On n’a pas donné de critère pour distinguer
![]() $X^{+}(a,e,u)$
de
$X^{+}(a,e,u)$
de
![]() $X^{-}(a,e,u)$
. On voit que l’on peut effectuer ces choix de signes de sorte que, pour
$X^{-}(a,e,u)$
. On voit que l’on peut effectuer ces choix de signes de sorte que, pour
![]() $\unicode[STIX]{x1D701}$
fixé et quand
$\unicode[STIX]{x1D701}$
fixé et quand
![]() $e$
et
$e$
et
![]() $u$
varient, les éléments
$u$
varient, les éléments
![]() $X^{\unicode[STIX]{x1D701}}(a,e,u)$
décrivent un ensemble de représentants des classes de conjugaison contenues dans l’une de nos deux classes totales de conjugaison stable. On fixe un élément dans cette classe qui appartienne à
$X^{\unicode[STIX]{x1D701}}(a,e,u)$
décrivent un ensemble de représentants des classes de conjugaison contenues dans l’une de nos deux classes totales de conjugaison stable. On fixe un élément dans cette classe qui appartienne à
![]() $\mathfrak{g}_{\operatorname{iso}}(F)$
et on le note
$\mathfrak{g}_{\operatorname{iso}}(F)$
et on le note
![]() $X^{\unicode[STIX]{x1D701}}(a,w^{\prime },w^{\prime \prime })$
.
$X^{\unicode[STIX]{x1D701}}(a,w^{\prime },w^{\prime \prime })$
.
On a défini
![]() $t_{1}^{\prime }$
,
$t_{1}^{\prime }$
,
![]() $t_{1}^{\prime \prime }$
,
$t_{1}^{\prime \prime }$
,
![]() $t_{2}^{\prime }$
,
$t_{2}^{\prime }$
,
![]() $t_{2}^{\prime \prime }$
en 2.2. On a les égalités
$t_{2}^{\prime \prime }$
en 2.2. On a les égalités
![]() $t_{1}^{\prime }=t_{1}^{\prime \prime }=(R+r)/2$
et
$t_{1}^{\prime }=t_{1}^{\prime \prime }=(R+r)/2$
et
![]() $t_{2}^{\prime }=t_{2}^{\prime \prime }=(R-r)/2$
. Fixons
$t_{2}^{\prime }=t_{2}^{\prime \prime }=(R-r)/2$
. Fixons
![]() $(L_{1},L_{2})\in {\mathcal{L}}$
. Soit
$(L_{1},L_{2})\in {\mathcal{L}}$
. Soit
![]() $\unicode[STIX]{x1D6FE}\in \unicode[STIX]{x1D6E4}$
. On définit deux suites
$\unicode[STIX]{x1D6FE}\in \unicode[STIX]{x1D6E4}$
. On définit deux suites
![]() $\unicode[STIX]{x1D6FE}^{L_{1}}=(\unicode[STIX]{x1D6FE}_{j}^{L_{1}})_{j=1,\ldots ,t_{1}^{\prime }}$
et
$\unicode[STIX]{x1D6FE}^{L_{1}}=(\unicode[STIX]{x1D6FE}_{j}^{L_{1}})_{j=1,\ldots ,t_{1}^{\prime }}$
et
![]() $\unicode[STIX]{x1D6FE}^{L_{2}}=(\unicode[STIX]{x1D6FE}_{j}^{L_{2}})_{j=1,\ldots ,t_{2}^{\prime }}$
par les formules suivantes :
$\unicode[STIX]{x1D6FE}^{L_{2}}=(\unicode[STIX]{x1D6FE}_{j}^{L_{2}})_{j=1,\ldots ,t_{2}^{\prime }}$
par les formules suivantes :
pour
![]() $j\in \{1,\ldots ,(R-r)/2\}$
,
$j\in \{1,\ldots ,(R-r)/2\}$
,
![]() $\unicode[STIX]{x1D6FE}_{j}^{L_{1}}=\unicode[STIX]{x1D6FE}_{l_{1}(j)}$
,
$\unicode[STIX]{x1D6FE}_{j}^{L_{1}}=\unicode[STIX]{x1D6FE}_{l_{1}(j)}$
,
![]() $\unicode[STIX]{x1D6FE}_{j}^{L_{2}}=\unicode[STIX]{x1D6FE}_{l_{2}(j)}$
;
$\unicode[STIX]{x1D6FE}_{j}^{L_{2}}=\unicode[STIX]{x1D6FE}_{l_{2}(j)}$
;
pour
![]() $j\in \{(R-r)/2+1,\ldots ,(R+r)/2\}$
,
$j\in \{(R-r)/2+1,\ldots ,(R+r)/2\}$
,
![]() $\unicode[STIX]{x1D6FE}_{j}^{L_{1}}=\unicode[STIX]{x1D6FE}_{j+(R-r)/2}$
.
$\unicode[STIX]{x1D6FE}_{j}^{L_{1}}=\unicode[STIX]{x1D6FE}_{j+(R-r)/2}$
.
Pour
![]() $a\in A(\unicode[STIX]{x1D6FE})$
, on définit de même des suites
$a\in A(\unicode[STIX]{x1D6FE})$
, on définit de même des suites
![]() $a^{L_{1}}=(a_{j}^{L_{1}})_{j=1,\ldots ,t_{1}^{\prime }}$
et
$a^{L_{1}}=(a_{j}^{L_{1}})_{j=1,\ldots ,t_{1}^{\prime }}$
et
![]() $a^{L_{2}}=(a_{j}^{L_{2}})_{j=1,\ldots ,t_{2}^{\prime }}$
. On définit un élément
$a^{L_{2}}=(a_{j}^{L_{2}})_{j=1,\ldots ,t_{2}^{\prime }}$
. On définit un élément
![]() $\unicode[STIX]{x1D702}[L_{2},\unicode[STIX]{x1D6FE}]\in F^{\times }/F^{\times 2}$
par les deux propriétés :
$\unicode[STIX]{x1D702}[L_{2},\unicode[STIX]{x1D6FE}]\in F^{\times }/F^{\times 2}$
par les deux propriétés :
![]() $\operatorname{val}_{F}(\unicode[STIX]{x1D702}[L_{2},\unicode[STIX]{x1D6FE}])\equiv t_{2}^{\prime }\,\,\text{mod}\,\,2\,\mathbb{Z}$
;
$\operatorname{val}_{F}(\unicode[STIX]{x1D702}[L_{2},\unicode[STIX]{x1D6FE}])\equiv t_{2}^{\prime }\,\,\text{mod}\,\,2\,\mathbb{Z}$
;
![]() $\operatorname{sgn}(\unicode[STIX]{x1D702}[L_{2},\unicode[STIX]{x1D6FE}]\unicode[STIX]{x1D71B}^{-\operatorname{val}_{F}(\unicode[STIX]{x1D702}[L_{2},\unicode[STIX]{x1D6FE}])}\prod _{j=1,\ldots ,t_{2}^{\prime }}\unicode[STIX]{x1D6FE}_{j}^{L_{2}})=\operatorname{sgn}_{CD}(w^{\prime \prime })$
.
$\operatorname{sgn}(\unicode[STIX]{x1D702}[L_{2},\unicode[STIX]{x1D6FE}]\unicode[STIX]{x1D71B}^{-\operatorname{val}_{F}(\unicode[STIX]{x1D702}[L_{2},\unicode[STIX]{x1D6FE}])}\prod _{j=1,\ldots ,t_{2}^{\prime }}\unicode[STIX]{x1D6FE}_{j}^{L_{2}})=\operatorname{sgn}_{CD}(w^{\prime \prime })$
.
On définit
![]() $\unicode[STIX]{x1D702}[L_{1},\unicode[STIX]{x1D6FE}]$
par l’égalité
$\unicode[STIX]{x1D702}[L_{1},\unicode[STIX]{x1D6FE}]$
par l’égalité
![]() $\unicode[STIX]{x1D702}[L_{1},\unicode[STIX]{x1D6FE}]\unicode[STIX]{x1D702}[L_{2},\unicode[STIX]{x1D6FE}]=\unicode[STIX]{x1D702}$
. On constate que les données
$\unicode[STIX]{x1D702}[L_{1},\unicode[STIX]{x1D6FE}]\unicode[STIX]{x1D702}[L_{2},\unicode[STIX]{x1D6FE}]=\unicode[STIX]{x1D702}$
. On constate que les données
![]() $\unicode[STIX]{x1D6FE}^{L_{1}}$
,
$\unicode[STIX]{x1D6FE}^{L_{1}}$
,
![]() $a^{L_{1}}$
,
$a^{L_{1}}$
,
![]() $(N^{\prime },0)$
,
$(N^{\prime },0)$
,
![]() $w_{1}^{\prime }=w^{\prime }$
et
$w_{1}^{\prime }=w^{\prime }$
et
![]() $w_{1}^{\prime \prime }=\emptyset$
vérifient les mêmes conditions que
$w_{1}^{\prime \prime }=\emptyset$
vérifient les mêmes conditions que
![]() $\unicode[STIX]{x1D6FE}$
,
$\unicode[STIX]{x1D6FE}$
,
![]() $a$
,
$a$
,
![]() $(N^{\prime },N^{\prime \prime })$
,
$(N^{\prime },N^{\prime \prime })$
,
![]() $w^{\prime }$
et
$w^{\prime }$
et
![]() $w^{\prime \prime }$
, le couple
$w^{\prime \prime }$
, le couple
![]() $(n,\unicode[STIX]{x1D702})$
étant remplacé par
$(n,\unicode[STIX]{x1D702})$
étant remplacé par
![]() $(n_{1},\unicode[STIX]{x1D702}[L_{1},\unicode[STIX]{x1D6FE}])$
. De même pour les données
$(n_{1},\unicode[STIX]{x1D702}[L_{1},\unicode[STIX]{x1D6FE}])$
. De même pour les données
![]() $\unicode[STIX]{x1D6FE}^{L_{2}}$
,
$\unicode[STIX]{x1D6FE}^{L_{2}}$
,
![]() $a^{L_{2}}$
,
$a^{L_{2}}$
,
![]() $(N^{\prime \prime },0)$
,
$(N^{\prime \prime },0)$
,
![]() $w_{2}^{\prime }=w^{\prime \prime }$
et
$w_{2}^{\prime }=w^{\prime \prime }$
et
![]() $w_{2}^{\prime \prime }=\emptyset$
, le couple
$w_{2}^{\prime \prime }=\emptyset$
, le couple
![]() $(n,\unicode[STIX]{x1D702})$
étant remplacé par
$(n,\unicode[STIX]{x1D702})$
étant remplacé par
![]() $(n_{2},\unicode[STIX]{x1D702}[L_{2},\unicode[STIX]{x1D6FE}])$
. De même que l’on a construit ci-dessus des éléments
$(n_{2},\unicode[STIX]{x1D702}[L_{2},\unicode[STIX]{x1D6FE}])$
. De même que l’on a construit ci-dessus des éléments
![]() $X^{\unicode[STIX]{x1D701}}(a,w^{\prime },w^{\prime \prime })$
, on construit dans
$X^{\unicode[STIX]{x1D701}}(a,w^{\prime },w^{\prime \prime })$
, on construit dans
![]() $\mathfrak{g}_{n_{1},\unicode[STIX]{x1D702}[L_{1},\unicode[STIX]{x1D6FE}],\operatorname{iso}}(F)$
un élément
$\mathfrak{g}_{n_{1},\unicode[STIX]{x1D702}[L_{1},\unicode[STIX]{x1D6FE}],\operatorname{iso}}(F)$
un élément
![]() $X^{\unicode[STIX]{x1D701}}(a^{L_{1}},w^{\prime })$
et dans
$X^{\unicode[STIX]{x1D701}}(a^{L_{1}},w^{\prime })$
et dans
![]() $\mathfrak{g}_{n_{2},\unicode[STIX]{x1D702}[L_{2},\unicode[STIX]{x1D6FE}],\operatorname{iso}}(F)$
un élément
$\mathfrak{g}_{n_{2},\unicode[STIX]{x1D702}[L_{2},\unicode[STIX]{x1D6FE}],\operatorname{iso}}(F)$
un élément
![]() $X^{\unicode[STIX]{x1D701}}(a^{L_{2}},w^{\prime \prime })$
. La correspondance endoscopique entre classes de conjugaison stable est un peu perturbée par les signes
$X^{\unicode[STIX]{x1D701}}(a^{L_{2}},w^{\prime \prime })$
. La correspondance endoscopique entre classes de conjugaison stable est un peu perturbée par les signes
![]() $\unicode[STIX]{x1D701}$
. Précisément, pour
$\unicode[STIX]{x1D701}$
. Précisément, pour
![]() $\unicode[STIX]{x1D701}_{1},\unicode[STIX]{x1D701}_{2}=\pm$
, il existe
$\unicode[STIX]{x1D701}_{1},\unicode[STIX]{x1D701}_{2}=\pm$
, il existe
![]() $\unicode[STIX]{x1D701}=\pm$
tel que la classe de conjugaison stable de
$\unicode[STIX]{x1D701}=\pm$
tel que la classe de conjugaison stable de
![]() $(X^{\unicode[STIX]{x1D701}_{1}}(a^{L_{1}},w^{\prime }),X^{\unicode[STIX]{x1D701}_{2}}(a^{L_{2}},w^{\prime \prime }))$
dans
$(X^{\unicode[STIX]{x1D701}_{1}}(a^{L_{1}},w^{\prime }),X^{\unicode[STIX]{x1D701}_{2}}(a^{L_{2}},w^{\prime \prime }))$
dans
![]() $\mathfrak{g}_{n_{1},\unicode[STIX]{x1D702}[L_{1},\unicode[STIX]{x1D6FE}],\operatorname{iso}}(F)\times \mathfrak{g}_{n_{2},\unicode[STIX]{x1D702}[L_{2},\unicode[STIX]{x1D6FE}],\operatorname{iso}}(F)$
corresponde à la classe totale de conjugaison stable de
$\mathfrak{g}_{n_{1},\unicode[STIX]{x1D702}[L_{1},\unicode[STIX]{x1D6FE}],\operatorname{iso}}(F)\times \mathfrak{g}_{n_{2},\unicode[STIX]{x1D702}[L_{2},\unicode[STIX]{x1D6FE}],\operatorname{iso}}(F)$
corresponde à la classe totale de conjugaison stable de
![]() $X^{\unicode[STIX]{x1D701}}(a,w^{\prime },w^{\prime \prime })$
. Ainsi, pour
$X^{\unicode[STIX]{x1D701}}(a,w^{\prime },w^{\prime \prime })$
. Ainsi, pour
![]() $e\in {\mathcal{E}}$
et
$e\in {\mathcal{E}}$
et
![]() $u\in {\mathcal{U}}$
, le facteur de transfert
$u\in {\mathcal{U}}$
, le facteur de transfert
![]() $\unicode[STIX]{x1D6E5}_{n_{1},\unicode[STIX]{x1D702}[L_{1},\unicode[STIX]{x1D6FE}],n_{2},\unicode[STIX]{x1D702}[L_{2},\unicode[STIX]{x1D6FE}]}((X^{\unicode[STIX]{x1D701}_{1}}(a^{L_{1}},w^{\prime }),X^{\unicode[STIX]{x1D701}_{2}}(a^{L_{2}},w^{\prime \prime })),X^{\unicode[STIX]{x1D701}}(a,e,u))$
est défini et non nul.
$\unicode[STIX]{x1D6E5}_{n_{1},\unicode[STIX]{x1D702}[L_{1},\unicode[STIX]{x1D6FE}],n_{2},\unicode[STIX]{x1D702}[L_{2},\unicode[STIX]{x1D6FE}]}((X^{\unicode[STIX]{x1D701}_{1}}(a^{L_{1}},w^{\prime }),X^{\unicode[STIX]{x1D701}_{2}}(a^{L_{2}},w^{\prime \prime })),X^{\unicode[STIX]{x1D701}}(a,e,u))$
est défini et non nul.
Remarque.
Il peut arriver que
![]() $n_{1}=0$
ou
$n_{1}=0$
ou
![]() $n_{2}=0$
. Dans ce cas, les termes
$n_{2}=0$
. Dans ce cas, les termes
![]() $X^{\unicode[STIX]{x1D701}_{1}}(a^{L_{1}},w^{\prime })$
ou
$X^{\unicode[STIX]{x1D701}_{1}}(a^{L_{1}},w^{\prime })$
ou
![]() $X^{\unicode[STIX]{x1D701}_{2}}(a^{L_{2}},w^{\prime \prime })$
disparaissent.
$X^{\unicode[STIX]{x1D701}_{2}}(a^{L_{2}},w^{\prime \prime })$
disparaissent.
Posons
 $$\begin{eqnarray}\displaystyle & & \displaystyle d(r^{\prime },r^{\prime \prime },\unicode[STIX]{x1D6FE},L_{2})\nonumber\\ \displaystyle & & \displaystyle \quad =\operatorname{sgn}(\unicode[STIX]{x1D702}\unicode[STIX]{x1D71B}^{-\operatorname{val}_{F}(\unicode[STIX]{x1D702})})^{(R-r)/2}\operatorname{sgn}_{CD}(w^{\prime })^{(R-r)/2}\operatorname{sgn}_{CD}(w^{\prime \prime })^{(R-r)/2+\operatorname{val}_{F}(\unicode[STIX]{x1D702})}\nonumber\\ \displaystyle & & \displaystyle \qquad \times \,\left(\displaystyle \mathop{\prod }_{j\in {\hat{J}}}\operatorname{sgn}(\unicode[STIX]{x1D6FE}_{j-1}\unicode[STIX]{x1D6FE}_{j})^{j/2-1}\operatorname{sgn}(\unicode[STIX]{x1D6FE}_{j-1}-\unicode[STIX]{x1D6FE}_{j})\right)\nonumber\\ \displaystyle & & \displaystyle \qquad \times \,\left(\displaystyle \mathop{\prod }_{j=R-r+1,\ldots ,R}\operatorname{sgn}(\unicode[STIX]{x1D6FE}_{j})^{(R-r)/2}\right)\nonumber\\ \displaystyle & & \displaystyle \qquad \times \,\operatorname{sgn}(-1)^{\operatorname{val}_{F}(\unicode[STIX]{x1D702}[L_{2},\unicode[STIX]{x1D6FE}])B}\operatorname{sgn}(\unicode[STIX]{x1D702}[L_{2},\unicode[STIX]{x1D6FE}]\unicode[STIX]{x1D71B}^{-\operatorname{val}_{F}(\unicode[STIX]{x1D702}[L_{2},\unicode[STIX]{x1D6FE}])})^{B}\operatorname{sgn}_{CD}(w^{\prime \prime })^{B},\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle d(r^{\prime },r^{\prime \prime },\unicode[STIX]{x1D6FE},L_{2})\nonumber\\ \displaystyle & & \displaystyle \quad =\operatorname{sgn}(\unicode[STIX]{x1D702}\unicode[STIX]{x1D71B}^{-\operatorname{val}_{F}(\unicode[STIX]{x1D702})})^{(R-r)/2}\operatorname{sgn}_{CD}(w^{\prime })^{(R-r)/2}\operatorname{sgn}_{CD}(w^{\prime \prime })^{(R-r)/2+\operatorname{val}_{F}(\unicode[STIX]{x1D702})}\nonumber\\ \displaystyle & & \displaystyle \qquad \times \,\left(\displaystyle \mathop{\prod }_{j\in {\hat{J}}}\operatorname{sgn}(\unicode[STIX]{x1D6FE}_{j-1}\unicode[STIX]{x1D6FE}_{j})^{j/2-1}\operatorname{sgn}(\unicode[STIX]{x1D6FE}_{j-1}-\unicode[STIX]{x1D6FE}_{j})\right)\nonumber\\ \displaystyle & & \displaystyle \qquad \times \,\left(\displaystyle \mathop{\prod }_{j=R-r+1,\ldots ,R}\operatorname{sgn}(\unicode[STIX]{x1D6FE}_{j})^{(R-r)/2}\right)\nonumber\\ \displaystyle & & \displaystyle \qquad \times \,\operatorname{sgn}(-1)^{\operatorname{val}_{F}(\unicode[STIX]{x1D702}[L_{2},\unicode[STIX]{x1D6FE}])B}\operatorname{sgn}(\unicode[STIX]{x1D702}[L_{2},\unicode[STIX]{x1D6FE}]\unicode[STIX]{x1D71B}^{-\operatorname{val}_{F}(\unicode[STIX]{x1D702}[L_{2},\unicode[STIX]{x1D6FE}])})^{B}\operatorname{sgn}_{CD}(w^{\prime \prime })^{B},\nonumber\end{eqnarray}$$
où
![]() $B=0$
si
$B=0$
si
![]() $r^{\prime }\geqslant r^{\prime \prime }$
ou
$r^{\prime }\geqslant r^{\prime \prime }$
ou
![]() $B=1$
si
$B=1$
si
![]() $r^{\prime }<r^{\prime \prime }$
.
$r^{\prime }<r^{\prime \prime }$
.
Lemme. Sous les hypothèses ci-dessus, on a l’égalité
Preuve.
Pour tout polynôme
![]() $Q$
, on note
$Q$
, on note
![]() $Q^{\prime }$
son polynôme dérivé. Notons
$Q^{\prime }$
son polynôme dérivé. Notons
![]() $P$
le polynôme caractéristique de
$P$
le polynôme caractéristique de
![]() $X^{\unicode[STIX]{x1D701}}(a,e,u)$
, vu comme endomorphisme de
$X^{\unicode[STIX]{x1D701}}(a,e,u)$
, vu comme endomorphisme de
![]() $V_{\sharp (a,e,u)}$
. Pour
$V_{\sharp (a,e,u)}$
. Pour
![]() $j\in \{1,\ldots ,t_{2}^{\prime }\}$
, posons
$j\in \{1,\ldots ,t_{2}^{\prime }\}$
, posons
et notons
![]() $\operatorname{sgn}_{l_{2}(j)}$
le caractère quadratique de
$\operatorname{sgn}_{l_{2}(j)}$
le caractère quadratique de
![]() $F_{l_{2}(j)}^{\natural }(\unicode[STIX]{x1D6FE})^{\times }$
associé à l’extension quadratique
$F_{l_{2}(j)}^{\natural }(\unicode[STIX]{x1D6FE})^{\times }$
associé à l’extension quadratique
![]() $F_{l_{2}(j)}(\unicode[STIX]{x1D6FE})$
. Pour
$F_{l_{2}(j)}(\unicode[STIX]{x1D6FE})$
. Pour
![]() $k\in K^{\prime \prime }$
, posons
$k\in K^{\prime \prime }$
, posons
et notons
![]() $\operatorname{sgn}_{k}$
le caractère quadratique de
$\operatorname{sgn}_{k}$
le caractère quadratique de
![]() $E_{k}^{\natural }$
associé à l’extension quadratique
$E_{k}^{\natural }$
associé à l’extension quadratique
![]() $E_{k}$
.
$E_{k}$
.
Remarque.
Les formules ci-dessus ne définissent
![]() $C_{l_{2}(j)}$
et
$C_{l_{2}(j)}$
et
![]() $C_{k}$
que modulo les groupes
$C_{k}$
que modulo les groupes
![]() $\operatorname{norme}_{F_{l_{2}(j)}(\unicode[STIX]{x1D6FE})/F_{l_{2}(j)}^{\natural }(\unicode[STIX]{x1D6FE})}(F_{l_{2}(j)}(\unicode[STIX]{x1D6FE})^{\times })$
, respectivement
$\operatorname{norme}_{F_{l_{2}(j)}(\unicode[STIX]{x1D6FE})/F_{l_{2}(j)}^{\natural }(\unicode[STIX]{x1D6FE})}(F_{l_{2}(j)}(\unicode[STIX]{x1D6FE})^{\times })$
, respectivement
![]() $\operatorname{norme}_{E_{k}/E_{k}^{\natural }}(E_{k}^{\times })$
. C’est sans importance pour la suite.
$\operatorname{norme}_{E_{k}/E_{k}^{\natural }}(E_{k}^{\times })$
. C’est sans importance pour la suite.
D’après [Reference Waldspurger9] proposition X.8, on a l’égalité
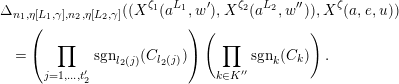 $$\begin{eqnarray}\displaystyle & & \displaystyle \unicode[STIX]{x1D6E5}_{n_{1},\unicode[STIX]{x1D702}[L_{1},\unicode[STIX]{x1D6FE}],n_{2},\unicode[STIX]{x1D702}[L_{2},\unicode[STIX]{x1D6FE}]}((X^{\unicode[STIX]{x1D701}_{1}}(a^{L_{1}},w^{\prime }),X^{\unicode[STIX]{x1D701}_{2}}(a^{L_{2}},w^{\prime \prime })),X^{\unicode[STIX]{x1D701}}(a,e,u))\nonumber\\ \displaystyle & & \displaystyle \quad =\left(\displaystyle \mathop{\prod }_{j=1,\ldots ,t_{2}^{\prime }}\operatorname{sgn}_{l_{2}(j)}(C_{l_{2}(j)})\right)\left(\displaystyle \mathop{\prod }_{k\in K^{\prime \prime }}\operatorname{sgn}_{k}(C_{k})\right).\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \unicode[STIX]{x1D6E5}_{n_{1},\unicode[STIX]{x1D702}[L_{1},\unicode[STIX]{x1D6FE}],n_{2},\unicode[STIX]{x1D702}[L_{2},\unicode[STIX]{x1D6FE}]}((X^{\unicode[STIX]{x1D701}_{1}}(a^{L_{1}},w^{\prime }),X^{\unicode[STIX]{x1D701}_{2}}(a^{L_{2}},w^{\prime \prime })),X^{\unicode[STIX]{x1D701}}(a,e,u))\nonumber\\ \displaystyle & & \displaystyle \quad =\left(\displaystyle \mathop{\prod }_{j=1,\ldots ,t_{2}^{\prime }}\operatorname{sgn}_{l_{2}(j)}(C_{l_{2}(j)})\right)\left(\displaystyle \mathop{\prod }_{k\in K^{\prime \prime }}\operatorname{sgn}_{k}(C_{k})\right).\end{eqnarray}$$
Pour
![]() $k\in K^{\prime \prime }$
, le caractère
$k\in K^{\prime \prime }$
, le caractère
![]() $\operatorname{sgn}_{k}$
est non ramifié. Pour calculer
$\operatorname{sgn}_{k}$
est non ramifié. Pour calculer
![]() $\operatorname{sgn}_{k}(C_{k})$
, il suffit de calculer la valuation de
$\operatorname{sgn}_{k}(C_{k})$
, il suffit de calculer la valuation de
![]() $C_{k}$
modulo
$C_{k}$
modulo
![]() $2\,\mathbb{Z}$
. On voit facilement que la valuation de
$2\,\mathbb{Z}$
. On voit facilement que la valuation de
![]() $(-1)^{n}[E_{k}:F]X_{k}^{-1}P^{\prime }(X_{k})$
est nulle. Celle de
$(-1)^{n}[E_{k}:F]X_{k}^{-1}P^{\prime }(X_{k})$
est nulle. Celle de
![]() $\unicode[STIX]{x1D702}\unicode[STIX]{x1D71B}u_{k}$
est
$\unicode[STIX]{x1D702}\unicode[STIX]{x1D71B}u_{k}$
est
![]() $\operatorname{val}_{F}(\unicode[STIX]{x1D702})+u_{k}$
. D’où
$\operatorname{val}_{F}(\unicode[STIX]{x1D702})+u_{k}$
. D’où
![]() $\operatorname{sgn}_{k}(C_{k})=(-1)^{\operatorname{val}_{F}(\unicode[STIX]{x1D702})+u_{k}}$
. Le produit des
$\operatorname{sgn}_{k}(C_{k})=(-1)^{\operatorname{val}_{F}(\unicode[STIX]{x1D702})+u_{k}}$
. Le produit des
![]() $(-1)^{u_{k}}$
pour
$(-1)^{u_{k}}$
pour
![]() $k\in K^{\prime \prime }$
est égal à
$k\in K^{\prime \prime }$
est égal à
![]() $\unicode[STIX]{x1D705}^{{\mathcal{U}}}(u)$
. Le produit des
$\unicode[STIX]{x1D705}^{{\mathcal{U}}}(u)$
. Le produit des
![]() $(-1)^{\operatorname{val}_{F}(\unicode[STIX]{x1D702})}$
est
$(-1)^{\operatorname{val}_{F}(\unicode[STIX]{x1D702})}$
est
![]() $(-1)^{|K^{\prime \prime }|\operatorname{val}_{F}(\unicode[STIX]{x1D702})}$
. Mais
$(-1)^{|K^{\prime \prime }|\operatorname{val}_{F}(\unicode[STIX]{x1D702})}$
. Mais
![]() $(-1)^{|K^{\prime \prime }|}=\operatorname{sgn}_{CD}(w^{\prime \prime })$
. D’où
$(-1)^{|K^{\prime \prime }|}=\operatorname{sgn}_{CD}(w^{\prime \prime })$
. D’où
Fixons
![]() $j=1,\ldots ,t_{2}^{\prime }$
. Posons pour simplifier
$j=1,\ldots ,t_{2}^{\prime }$
. Posons pour simplifier
![]() $l_{1}=l_{1}(j)$
,
$l_{1}=l_{1}(j)$
,
![]() $l_{2}=l_{2}(j)$
et notons
$l_{2}=l_{2}(j)$
et notons
![]() $l$
l’élément de
$l$
l’élément de
![]() ${\hat{J}}$
tel que
${\hat{J}}$
tel que
![]() $\{l_{1},l_{2}\}=\{l-1,l\}$
. Le polynôme
$\{l_{1},l_{2}\}=\{l-1,l\}$
. Le polynôme
![]() $P$
se décompose en produit des polynômes caractéristiques
$P$
se décompose en produit des polynômes caractéristiques
![]() $P_{k}$
des
$P_{k}$
des
![]() $X_{k}$
, pour
$X_{k}$
, pour
![]() $k=1,\ldots ,t$
, et des polynômes caractéristiques
$k=1,\ldots ,t$
, et des polynômes caractéristiques
![]() $P_{h}$
des
$P_{h}$
des
![]() $a_{h}$
, pour
$a_{h}$
, pour
![]() $h=1,\ldots ,R$
. On a
$h=1,\ldots ,R$
. On a
 $$\begin{eqnarray}P^{\prime }(a_{l_{2}})=P_{l_{2}}^{\prime }(a_{l_{2}})\left(\displaystyle \mathop{\prod }_{h=1,\ldots ,R;h\not =l_{2}}P_{h}(a_{l_{2}})\right)\left(\displaystyle \mathop{\prod }_{k=1,\ldots ,t}P_{k}(a_{l_{2}})\right).\end{eqnarray}$$
$$\begin{eqnarray}P^{\prime }(a_{l_{2}})=P_{l_{2}}^{\prime }(a_{l_{2}})\left(\displaystyle \mathop{\prod }_{h=1,\ldots ,R;h\not =l_{2}}P_{h}(a_{l_{2}})\right)\left(\displaystyle \mathop{\prod }_{k=1,\ldots ,t}P_{k}(a_{l_{2}})\right).\end{eqnarray}$$
On vérifie que tous les termes ci-dessus sauf le premier appartiennent à
![]() $F_{l_{2}}^{\natural }(\unicode[STIX]{x1D6FE})^{\times }$
. Pour le premier, son produit avec
$F_{l_{2}}^{\natural }(\unicode[STIX]{x1D6FE})^{\times }$
. Pour le premier, son produit avec
![]() $a_{l_{2}}$
appartient à ce groupe. On a calculé les images par
$a_{l_{2}}$
appartient à ce groupe. On a calculé les images par
![]() $\operatorname{sgn}_{l_{2}}$
de presque tous ces termes en [Reference Waldspurger9] page 400. Pour
$\operatorname{sgn}_{l_{2}}$
de presque tous ces termes en [Reference Waldspurger9] page 400. Pour
![]() $k=1,\ldots ,t$
, on a
$k=1,\ldots ,t$
, on a
![]() $\operatorname{sgn}_{l_{2}}(P_{k}(a_{l_{2}}))=-\text{sgn}(-1)^{[E_{k}:F]/2}$
. Parce que
$\operatorname{sgn}_{l_{2}}(P_{k}(a_{l_{2}}))=-\text{sgn}(-1)^{[E_{k}:F]/2}$
. Parce que
![]() $[E_{k}:F]/2=\unicode[STIX]{x1D6FD}_{k}$
, on a
$[E_{k}:F]/2=\unicode[STIX]{x1D6FD}_{k}$
, on a
![]() $\sum _{k=1,\ldots ,t}[E_{k}:F]/2=N$
. On a aussi
$\sum _{k=1,\ldots ,t}[E_{k}:F]/2=N$
. On a aussi
![]() $(-1)^{t}=\operatorname{sgn}_{CD}(w^{\prime })\operatorname{sgn}_{CD}(w^{\prime \prime })$
. On obtient
$(-1)^{t}=\operatorname{sgn}_{CD}(w^{\prime })\operatorname{sgn}_{CD}(w^{\prime \prime })$
. On obtient
 $$\begin{eqnarray}\operatorname{sgn}_{l_{2}}\left(\displaystyle \mathop{\prod }_{k=1,\ldots ,t}P_{k}(a_{l_{2}})\right)=\operatorname{sgn}(-1)^{N}\operatorname{sgn}_{CD}(w^{\prime })\operatorname{sgn}_{CD}(w^{\prime \prime }).\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{sgn}_{l_{2}}\left(\displaystyle \mathop{\prod }_{k=1,\ldots ,t}P_{k}(a_{l_{2}})\right)=\operatorname{sgn}(-1)^{N}\operatorname{sgn}_{CD}(w^{\prime })\operatorname{sgn}_{CD}(w^{\prime \prime }).\end{eqnarray}$$
Soit
![]() $h\in \{1,\ldots ,l-2\}$
. On a
$h\in \{1,\ldots ,l-2\}$
. On a
![]() $\operatorname{sgn}_{l_{2}}(P_{h}(a_{l_{2}}))=\operatorname{sgn}(-1)^{[F_{h}(\unicode[STIX]{x1D6FE}):F]/2}$
. Par construction, tous les
$\operatorname{sgn}_{l_{2}}(P_{h}(a_{l_{2}}))=\operatorname{sgn}(-1)^{[F_{h}(\unicode[STIX]{x1D6FE}):F]/2}$
. Par construction, tous les
![]() $[F_{h}(\unicode[STIX]{x1D6FE}):F]$
sont impairs et le terme ci-dessus vaut
$[F_{h}(\unicode[STIX]{x1D6FE}):F]$
sont impairs et le terme ci-dessus vaut
![]() $\operatorname{sgn}(-1)$
. Puisque
$\operatorname{sgn}(-1)$
. Puisque
![]() $l$
est pair, le produit de ces termes sur
$l$
est pair, le produit de ces termes sur
![]() $h=1,\ldots ,l-2$
vaut
$h=1,\ldots ,l-2$
vaut
![]() $1$
. Pour
$1$
. Pour
![]() $h\in \{l+1,\ldots ,R\}$
, on a
$h\in \{l+1,\ldots ,R\}$
, on a
![]() $\operatorname{sgn}_{l_{2}}(P_{h}(a_{l_{2}}))=\operatorname{sgn}(-1)^{1+[F_{l_{2}}(\unicode[STIX]{x1D6FE}):F]/2}\operatorname{sgn}(\unicode[STIX]{x1D6FE}_{l_{2}}\unicode[STIX]{x1D6FE}_{h})$
. Comme ci-dessus,
$\operatorname{sgn}_{l_{2}}(P_{h}(a_{l_{2}}))=\operatorname{sgn}(-1)^{1+[F_{l_{2}}(\unicode[STIX]{x1D6FE}):F]/2}\operatorname{sgn}(\unicode[STIX]{x1D6FE}_{l_{2}}\unicode[STIX]{x1D6FE}_{h})$
. Comme ci-dessus,
![]() $[F_{l_{2}}(\unicode[STIX]{x1D6FE}):F]/2$
est impair et le terme ci-dessus vaut
$[F_{l_{2}}(\unicode[STIX]{x1D6FE}):F]/2$
est impair et le terme ci-dessus vaut
![]() $\operatorname{sgn}(\unicode[STIX]{x1D6FE}_{l_{2}}\unicode[STIX]{x1D6FE}_{h})$
. Puisque
$\operatorname{sgn}(\unicode[STIX]{x1D6FE}_{l_{2}}\unicode[STIX]{x1D6FE}_{h})$
. Puisque
![]() $l$
est pair, le produit de ces termes sur
$l$
est pair, le produit de ces termes sur
![]() $h=l+1,\ldots ,R$
vaut
$h=l+1,\ldots ,R$
vaut
![]() $\operatorname{sgn}(\unicode[STIX]{x1D6FE}_{l_{2}})^{R}\prod _{h=l+1,\ldots ,R}\operatorname{sgn}(\unicode[STIX]{x1D6FE}_{h})$
. On a
$\operatorname{sgn}(\unicode[STIX]{x1D6FE}_{l_{2}})^{R}\prod _{h=l+1,\ldots ,R}\operatorname{sgn}(\unicode[STIX]{x1D6FE}_{h})$
. On a
![]() $\operatorname{sgn}_{l_{2}}(a_{l_{2}}P_{l_{2}}^{\prime }(a_{l_{2}}))=\operatorname{sgn}((-1)^{[F_{l_{2}}/F]/2}[F_{l_{2}}:F])$
, ou encore
$\operatorname{sgn}_{l_{2}}(a_{l_{2}}P_{l_{2}}^{\prime }(a_{l_{2}}))=\operatorname{sgn}((-1)^{[F_{l_{2}}/F]/2}[F_{l_{2}}:F])$
, ou encore
![]() $\operatorname{sgn}(-[F_{l_{2}}:F])$
. Il reste un dernier terme
$\operatorname{sgn}(-[F_{l_{2}}:F])$
. Il reste un dernier terme
![]() $P_{l_{1}}(a_{l_{2}})$
, dont l’image par
$P_{l_{1}}(a_{l_{2}})$
, dont l’image par
![]() $\operatorname{sgn}_{l_{2}}$
n’est pas calculée dans [Reference Waldspurger9]. Le polynôme caractéristique de
$\operatorname{sgn}_{l_{2}}$
n’est pas calculée dans [Reference Waldspurger9]. Le polynôme caractéristique de
![]() $a_{l_{1}}$
est
$a_{l_{1}}$
est
![]() $P_{l_{1}}(Y)=Y^{2l-2}-\unicode[STIX]{x1D71B}\unicode[STIX]{x1D6FE}_{l_{1}}$
. Donc
$P_{l_{1}}(Y)=Y^{2l-2}-\unicode[STIX]{x1D71B}\unicode[STIX]{x1D6FE}_{l_{1}}$
. Donc
![]() $P_{l_{1}}(a_{l_{2}})=a_{l_{2}}^{2l-2}-\unicode[STIX]{x1D71B}\unicode[STIX]{x1D6FE}_{l_{1}}=\unicode[STIX]{x1D71B}(\unicode[STIX]{x1D6FE}_{l_{2}}-\unicode[STIX]{x1D6FE}_{l_{1}})$
. Mais
$P_{l_{1}}(a_{l_{2}})=a_{l_{2}}^{2l-2}-\unicode[STIX]{x1D71B}\unicode[STIX]{x1D6FE}_{l_{1}}=\unicode[STIX]{x1D71B}(\unicode[STIX]{x1D6FE}_{l_{2}}-\unicode[STIX]{x1D6FE}_{l_{1}})$
. Mais
![]() $-\unicode[STIX]{x1D71B}^{-1}\unicode[STIX]{x1D6FE}_{l_{2}}$
est une norme de l’extension
$-\unicode[STIX]{x1D71B}^{-1}\unicode[STIX]{x1D6FE}_{l_{2}}$
est une norme de l’extension
![]() $F_{l_{2}}(\unicode[STIX]{x1D6FE})/F_{l_{2}}^{\natural }(\unicode[STIX]{x1D6FE})$
(c’est la norme de
$F_{l_{2}}(\unicode[STIX]{x1D6FE})/F_{l_{2}}^{\natural }(\unicode[STIX]{x1D6FE})$
(c’est la norme de
![]() $\unicode[STIX]{x1D71B}^{-1}a_{l_{2}}^{l-1}$
). On a donc
$\unicode[STIX]{x1D71B}^{-1}a_{l_{2}}^{l-1}$
). On a donc
puisque
![]() $\operatorname{sgn}_{l_{2}}$
coïncide avec
$\operatorname{sgn}_{l_{2}}$
coïncide avec
![]() $\operatorname{sgn}$
sur
$\operatorname{sgn}$
sur
![]() $\mathfrak{o}^{\times }$
. En rassemblant ces calculs, on obtient
$\mathfrak{o}^{\times }$
. En rassemblant ces calculs, on obtient
 $$\begin{eqnarray}\displaystyle & & \displaystyle \operatorname{sgn}_{a_{l_{2}}}(a_{l_{2}}P^{\prime }(a_{l_{2}}))\nonumber\\ \displaystyle & & \displaystyle \quad =\operatorname{sgn}(-1)^{N}\operatorname{sgn}_{CD}(w^{\prime })\operatorname{sgn}_{CD}(w^{\prime \prime })\operatorname{sgn}([F_{l_{2}}(\unicode[STIX]{x1D6FE}):F])\operatorname{sgn}(\unicode[STIX]{x1D6FE}_{l_{2}}-\unicode[STIX]{x1D6FE}_{l_{1}})\nonumber\\ \displaystyle & & \displaystyle \qquad \times \,\operatorname{sgn}(\unicode[STIX]{x1D6FE}_{l_{2}})^{R+1}\displaystyle \mathop{\prod }_{h=l+1,\ldots ,R}\operatorname{sgn}(\unicode[STIX]{x1D6FE}_{h}).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \operatorname{sgn}_{a_{l_{2}}}(a_{l_{2}}P^{\prime }(a_{l_{2}}))\nonumber\\ \displaystyle & & \displaystyle \quad =\operatorname{sgn}(-1)^{N}\operatorname{sgn}_{CD}(w^{\prime })\operatorname{sgn}_{CD}(w^{\prime \prime })\operatorname{sgn}([F_{l_{2}}(\unicode[STIX]{x1D6FE}):F])\operatorname{sgn}(\unicode[STIX]{x1D6FE}_{l_{2}}-\unicode[STIX]{x1D6FE}_{l_{1}})\nonumber\\ \displaystyle & & \displaystyle \qquad \times \,\operatorname{sgn}(\unicode[STIX]{x1D6FE}_{l_{2}})^{R+1}\displaystyle \mathop{\prod }_{h=l+1,\ldots ,R}\operatorname{sgn}(\unicode[STIX]{x1D6FE}_{h}).\nonumber\end{eqnarray}$$
Le terme
![]() $C_{l_{2}}$
est le produit de
$C_{l_{2}}$
est le produit de
![]() $a_{l_{2}}P^{\prime }(a_{l_{2}})$
et de
$a_{l_{2}}P^{\prime }(a_{l_{2}})$
et de
![]() $(-1)^{n}\unicode[STIX]{x1D702}[F_{l_{2}}(\unicode[STIX]{x1D6FE}):F]c[\unicode[STIX]{x1D6FE},e]_{l_{2}}a_{l_{2}}^{-2}$
. Le terme
$(-1)^{n}\unicode[STIX]{x1D702}[F_{l_{2}}(\unicode[STIX]{x1D6FE}):F]c[\unicode[STIX]{x1D6FE},e]_{l_{2}}a_{l_{2}}^{-2}$
. Le terme
![]() $a_{l_{2}}^{-2}$
est remplacé par
$a_{l_{2}}^{-2}$
est remplacé par
![]() $-1$
car
$-1$
car
![]() $-a_{l_{2}}^{-2}$
est la norme de
$-a_{l_{2}}^{-2}$
est la norme de
![]() $a_{l_{2}}^{-1}$
. Le facteur
$a_{l_{2}}^{-1}$
. Le facteur
![]() $[F_{l_{2}}(\unicode[STIX]{x1D6FE}):F]$
compense celui intervenant dans la formule précédente. On a
$[F_{l_{2}}(\unicode[STIX]{x1D6FE}):F]$
compense celui intervenant dans la formule précédente. On a
Le premier facteur est remplacé par
![]() $\operatorname{sgn}(\unicode[STIX]{x1D702}\unicode[STIX]{x1D71B}^{-\operatorname{val}_{F}(\unicode[STIX]{x1D702})})$
. Puisque
$\operatorname{sgn}(\unicode[STIX]{x1D702}\unicode[STIX]{x1D71B}^{-\operatorname{val}_{F}(\unicode[STIX]{x1D702})})$
. Puisque
![]() $-\unicode[STIX]{x1D71B}^{-1}\unicode[STIX]{x1D6FE}_{l_{2}}$
est une norme, le second facteur est remplacé par
$-\unicode[STIX]{x1D71B}^{-1}\unicode[STIX]{x1D6FE}_{l_{2}}$
est une norme, le second facteur est remplacé par
![]() $\operatorname{sgn}(-\unicode[STIX]{x1D6FE}_{l_{2}})^{\operatorname{val}_{F}(\unicode[STIX]{x1D702})}$
, ou encore, puisque
$\operatorname{sgn}(-\unicode[STIX]{x1D6FE}_{l_{2}})^{\operatorname{val}_{F}(\unicode[STIX]{x1D702})}$
, ou encore, puisque
![]() $\operatorname{val}_{F}(\unicode[STIX]{x1D702})$
est de la même parité que
$\operatorname{val}_{F}(\unicode[STIX]{x1D702})$
est de la même parité que
![]() $R$
, par
$R$
, par
![]() $\operatorname{sgn}(-\unicode[STIX]{x1D6FE}_{l_{2}})^{R}$
. En se reportant à la définition de
$\operatorname{sgn}(-\unicode[STIX]{x1D6FE}_{l_{2}})^{R}$
. En se reportant à la définition de
![]() $c[\unicode[STIX]{x1D6FE},e]_{l_{2}}$
, on peut écrire
$c[\unicode[STIX]{x1D6FE},e]_{l_{2}}$
, on peut écrire
![]() $c[\unicode[STIX]{x1D6FE},e]_{l_{2}}=(-1)^{l_{2}}\unicode[STIX]{x1D6FE}_{l_{2}}e_{l_{2}}(-\unicode[STIX]{x1D6FE}_{l_{2}})^{B}$
, où
$c[\unicode[STIX]{x1D6FE},e]_{l_{2}}=(-1)^{l_{2}}\unicode[STIX]{x1D6FE}_{l_{2}}e_{l_{2}}(-\unicode[STIX]{x1D6FE}_{l_{2}})^{B}$
, où
![]() $B$
a été défini avant l’énoncé. D’où
$B$
a été défini avant l’énoncé. D’où
On obtient alors
 $$\begin{eqnarray}\displaystyle \operatorname{sgn}_{l_{2}}(C_{l_{2}}) & = & \displaystyle \operatorname{sgn}(-1)^{N+n+R+1+l_{2}}\operatorname{sgn}(\unicode[STIX]{x1D702}\unicode[STIX]{x1D71B}^{-\operatorname{val}_{F}(\unicode[STIX]{x1D702})})\operatorname{sgn}_{CD}(w^{\prime })\operatorname{sgn}_{CD}(w^{\prime \prime })\nonumber\\ \displaystyle & & \displaystyle \times \,\operatorname{sgn}(e_{l_{2}})\operatorname{sgn}(\unicode[STIX]{x1D6FE}_{l_{2}}-\unicode[STIX]{x1D6FE}_{l_{1}})\nonumber\\ \displaystyle & & \displaystyle \times \,\operatorname{sgn}(-\unicode[STIX]{x1D6FE}_{l_{2}})^{B}\displaystyle \mathop{\prod }_{h=l+1,\ldots ,R}\operatorname{sgn}(\unicode[STIX]{x1D6FE}_{h}).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \operatorname{sgn}_{l_{2}}(C_{l_{2}}) & = & \displaystyle \operatorname{sgn}(-1)^{N+n+R+1+l_{2}}\operatorname{sgn}(\unicode[STIX]{x1D702}\unicode[STIX]{x1D71B}^{-\operatorname{val}_{F}(\unicode[STIX]{x1D702})})\operatorname{sgn}_{CD}(w^{\prime })\operatorname{sgn}_{CD}(w^{\prime \prime })\nonumber\\ \displaystyle & & \displaystyle \times \,\operatorname{sgn}(e_{l_{2}})\operatorname{sgn}(\unicode[STIX]{x1D6FE}_{l_{2}}-\unicode[STIX]{x1D6FE}_{l_{1}})\nonumber\\ \displaystyle & & \displaystyle \times \,\operatorname{sgn}(-\unicode[STIX]{x1D6FE}_{l_{2}})^{B}\displaystyle \mathop{\prod }_{h=l+1,\ldots ,R}\operatorname{sgn}(\unicode[STIX]{x1D6FE}_{h}).\nonumber\end{eqnarray}$$
On a
![]() $n-N=(r^{\prime 2}+r^{\prime \prime 2})/2$
. Puisque
$n-N=(r^{\prime 2}+r^{\prime \prime 2})/2$
. Puisque
![]() $r^{\prime }$
et
$r^{\prime }$
et
![]() $r^{\prime \prime }$
sont de même parité, on constate que
$r^{\prime \prime }$
sont de même parité, on constate que
![]() $n-N$
est de la même parité que
$n-N$
est de la même parité que
![]() $r^{\prime }$
et
$r^{\prime }$
et
![]() $r^{\prime \prime }$
, ou encore de
$r^{\prime \prime }$
, ou encore de
![]() $R$
. Le premier terme se simplifie donc en
$R$
. Le premier terme se simplifie donc en
![]() $\operatorname{sgn}(-1)^{1+l_{2}}$
. On constate aussi que
$\operatorname{sgn}(-1)^{1+l_{2}}$
. On constate aussi que
![]() $(-1)^{1+l_{2}}(\unicode[STIX]{x1D6FE}_{l_{2}}-\unicode[STIX]{x1D6FE}_{l_{1}})=\unicode[STIX]{x1D6FE}_{l-1}-\unicode[STIX]{x1D6FE}_{l}$
. D’où
$(-1)^{1+l_{2}}(\unicode[STIX]{x1D6FE}_{l_{2}}-\unicode[STIX]{x1D6FE}_{l_{1}})=\unicode[STIX]{x1D6FE}_{l-1}-\unicode[STIX]{x1D6FE}_{l}$
. D’où
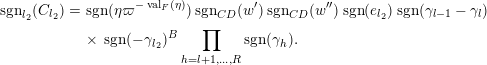 $$\begin{eqnarray}\displaystyle \operatorname{sgn}_{l_{2}}(C_{l_{2}}) & = & \displaystyle \operatorname{sgn}(\unicode[STIX]{x1D702}\unicode[STIX]{x1D71B}^{-\operatorname{val}_{F}(\unicode[STIX]{x1D702})})\operatorname{sgn}_{CD}(w^{\prime })\operatorname{sgn}_{CD}(w^{\prime \prime })\operatorname{sgn}(e_{l_{2}})\operatorname{sgn}(\unicode[STIX]{x1D6FE}_{l-1}-\unicode[STIX]{x1D6FE}_{l})\nonumber\\ \displaystyle & & \displaystyle \times \,\operatorname{sgn}(-\unicode[STIX]{x1D6FE}_{l_{2}})^{B}\displaystyle \mathop{\prod }_{h=l+1,\ldots ,R}\operatorname{sgn}(\unicode[STIX]{x1D6FE}_{h}).\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \operatorname{sgn}_{l_{2}}(C_{l_{2}}) & = & \displaystyle \operatorname{sgn}(\unicode[STIX]{x1D702}\unicode[STIX]{x1D71B}^{-\operatorname{val}_{F}(\unicode[STIX]{x1D702})})\operatorname{sgn}_{CD}(w^{\prime })\operatorname{sgn}_{CD}(w^{\prime \prime })\operatorname{sgn}(e_{l_{2}})\operatorname{sgn}(\unicode[STIX]{x1D6FE}_{l-1}-\unicode[STIX]{x1D6FE}_{l})\nonumber\\ \displaystyle & & \displaystyle \times \,\operatorname{sgn}(-\unicode[STIX]{x1D6FE}_{l_{2}})^{B}\displaystyle \mathop{\prod }_{h=l+1,\ldots ,R}\operatorname{sgn}(\unicode[STIX]{x1D6FE}_{h}).\end{eqnarray}$$
Rétablissons l’indice
![]() $j$
et faisons le produit de ces expressions sur
$j$
et faisons le produit de ces expressions sur
![]() $j=1,\ldots ,t_{2}^{\prime }=(R-r)/2$
. Les premiers termes donnent
$j=1,\ldots ,t_{2}^{\prime }=(R-r)/2$
. Les premiers termes donnent
![]() $\operatorname{sgn}(\unicode[STIX]{x1D702}\unicode[STIX]{x1D71B}^{-\operatorname{val}_{F}(\unicode[STIX]{x1D702})})^{(R-r)/2}\operatorname{sgn}_{CD}(w^{\prime })^{(R-r)/2}\operatorname{sgn}_{CD}(w^{\prime \prime })^{(R-r)/2}$
. Le produit des
$\operatorname{sgn}(\unicode[STIX]{x1D702}\unicode[STIX]{x1D71B}^{-\operatorname{val}_{F}(\unicode[STIX]{x1D702})})^{(R-r)/2}\operatorname{sgn}_{CD}(w^{\prime })^{(R-r)/2}\operatorname{sgn}_{CD}(w^{\prime \prime })^{(R-r)/2}$
. Le produit des
![]() $\operatorname{sgn}(e_{l_{2}(j)})$
est égal à
$\operatorname{sgn}(e_{l_{2}(j)})$
est égal à
![]() $\unicode[STIX]{x1D705}^{L_{2}}(e)$
. Le produit des termes suivants est
$\unicode[STIX]{x1D705}^{L_{2}}(e)$
. Le produit des termes suivants est
![]() $\prod _{j\in {\hat{J}}}\operatorname{sgn}(\unicode[STIX]{x1D6FE}_{j-1}-\unicode[STIX]{x1D6FE}_{j})$
. On a
$\prod _{j\in {\hat{J}}}\operatorname{sgn}(\unicode[STIX]{x1D6FE}_{j-1}-\unicode[STIX]{x1D6FE}_{j})$
. On a
 $$\begin{eqnarray}\displaystyle \mathop{\prod }_{j=1,\ldots ,t_{2}^{\prime }}\operatorname{sgn}(-\unicode[STIX]{x1D6FE}_{l_{2}(j)})=\operatorname{sgn}(-1)^{t_{2}^{\prime }}\operatorname{sgn}\left(\displaystyle \mathop{\prod }_{j=1,\ldots ,t_{2}^{\prime }}\unicode[STIX]{x1D6FE}_{j}^{L_{2}}\right).\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \mathop{\prod }_{j=1,\ldots ,t_{2}^{\prime }}\operatorname{sgn}(-\unicode[STIX]{x1D6FE}_{l_{2}(j)})=\operatorname{sgn}(-1)^{t_{2}^{\prime }}\operatorname{sgn}\left(\displaystyle \mathop{\prod }_{j=1,\ldots ,t_{2}^{\prime }}\unicode[STIX]{x1D6FE}_{j}^{L_{2}}\right).\end{eqnarray}$$
Puisque
![]() $t_{2}^{\prime }$
est de la même parité que
$t_{2}^{\prime }$
est de la même parité que
![]() $\operatorname{val}_{F}(\unicode[STIX]{x1D702}[L_{2},\unicode[STIX]{x1D6FE}])$
, le premier terme vaut
$\operatorname{val}_{F}(\unicode[STIX]{x1D702}[L_{2},\unicode[STIX]{x1D6FE}])$
, le premier terme vaut
![]() $\operatorname{sgn}(-1)^{\operatorname{val}_{F}(\unicode[STIX]{x1D702}[L_{2},\unicode[STIX]{x1D6FE}])}$
. Par définition de
$\operatorname{sgn}(-1)^{\operatorname{val}_{F}(\unicode[STIX]{x1D702}[L_{2},\unicode[STIX]{x1D6FE}])}$
. Par définition de
![]() $\unicode[STIX]{x1D702}[L_{2},\unicode[STIX]{x1D6FE}]$
, le second terme vaut
$\unicode[STIX]{x1D702}[L_{2},\unicode[STIX]{x1D6FE}]$
, le second terme vaut
![]() $\operatorname{sgn}(\unicode[STIX]{x1D702}[L_{2},\unicode[STIX]{x1D6FE}]\unicode[STIX]{x1D71B}^{-\operatorname{val}_{F}(\unicode[STIX]{x1D702}[L_{2},\unicode[STIX]{x1D6FE}])})\operatorname{sgn}_{CD}(w^{\prime \prime })$
. Considérons le dernier produit de la formule (3). Pour
$\operatorname{sgn}(\unicode[STIX]{x1D702}[L_{2},\unicode[STIX]{x1D6FE}]\unicode[STIX]{x1D71B}^{-\operatorname{val}_{F}(\unicode[STIX]{x1D702}[L_{2},\unicode[STIX]{x1D6FE}])})\operatorname{sgn}_{CD}(w^{\prime \prime })$
. Considérons le dernier produit de la formule (3). Pour
![]() $h\in \{R-r+1,\ldots ,R\}$
, le terme
$h\in \{R-r+1,\ldots ,R\}$
, le terme
![]() $\operatorname{sgn}(\unicode[STIX]{x1D6FE}_{h})$
intervient pour tout
$\operatorname{sgn}(\unicode[STIX]{x1D6FE}_{h})$
intervient pour tout
![]() $j$
. Le produit en
$j$
. Le produit en
![]() $j$
donne
$j$
donne
![]() $\operatorname{sgn}(\unicode[STIX]{x1D6FE}_{h})^{(R-r)/2}$
. Pour
$\operatorname{sgn}(\unicode[STIX]{x1D6FE}_{h})^{(R-r)/2}$
. Pour
![]() $h\in {\hat{J}}$
, les termes
$h\in {\hat{J}}$
, les termes
![]() $\operatorname{sgn}(\unicode[STIX]{x1D6FE}_{h-1})$
et
$\operatorname{sgn}(\unicode[STIX]{x1D6FE}_{h-1})$
et
![]() $\operatorname{sgn}(\unicode[STIX]{x1D6FE}_{h})$
interviennent pour les
$\operatorname{sgn}(\unicode[STIX]{x1D6FE}_{h})$
interviennent pour les
![]() $j<h/2$
. Le produit donne
$j<h/2$
. Le produit donne
![]() $\operatorname{sgn}(\unicode[STIX]{x1D6FE}_{h-1}\unicode[STIX]{x1D6FE}_{h})^{h/2-1}$
. D’où
$\operatorname{sgn}(\unicode[STIX]{x1D6FE}_{h-1}\unicode[STIX]{x1D6FE}_{h})^{h/2-1}$
. D’où
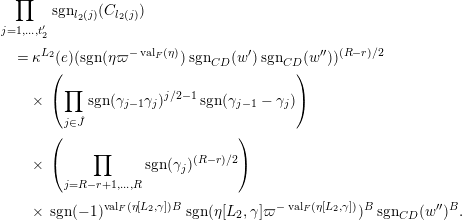 $$\begin{eqnarray}\displaystyle & & \displaystyle \displaystyle \mathop{\prod }_{j=1,\ldots ,t_{2}^{\prime }}\operatorname{sgn}_{l_{2}(j)}(C_{l_{2}(j)})\nonumber\\ \displaystyle & & \displaystyle \quad =\unicode[STIX]{x1D705}^{L_{2}}(e)(\operatorname{sgn}(\unicode[STIX]{x1D702}\unicode[STIX]{x1D71B}^{-\operatorname{val}_{F}(\unicode[STIX]{x1D702})})\operatorname{sgn}_{CD}(w^{\prime })\operatorname{sgn}_{CD}(w^{\prime \prime }))^{(R-r)/2}\nonumber\\ \displaystyle & & \displaystyle \qquad \times \,\left(\displaystyle \mathop{\prod }_{j\in {\hat{J}}}\operatorname{sgn}(\unicode[STIX]{x1D6FE}_{j-1}\unicode[STIX]{x1D6FE}_{j})^{j/2-1}\operatorname{sgn}(\unicode[STIX]{x1D6FE}_{j-1}-\unicode[STIX]{x1D6FE}_{j})\right)\nonumber\\ \displaystyle & & \displaystyle \qquad \times \,\left(\displaystyle \mathop{\prod }_{j=R-r+1,\ldots ,R}\operatorname{sgn}(\unicode[STIX]{x1D6FE}_{j})^{(R-r)/2}\right)\nonumber\\ \displaystyle & & \displaystyle \qquad \times \,\operatorname{sgn}(-1)^{\operatorname{val}_{F}(\unicode[STIX]{x1D702}[L_{2},\unicode[STIX]{x1D6FE}])B}\operatorname{sgn}(\unicode[STIX]{x1D702}[L_{2},\unicode[STIX]{x1D6FE}]\unicode[STIX]{x1D71B}^{-\operatorname{val}_{F}(\unicode[STIX]{x1D702}[L_{2},\unicode[STIX]{x1D6FE}])})^{B}\operatorname{sgn}_{CD}(w^{\prime \prime })^{B}.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \displaystyle \mathop{\prod }_{j=1,\ldots ,t_{2}^{\prime }}\operatorname{sgn}_{l_{2}(j)}(C_{l_{2}(j)})\nonumber\\ \displaystyle & & \displaystyle \quad =\unicode[STIX]{x1D705}^{L_{2}}(e)(\operatorname{sgn}(\unicode[STIX]{x1D702}\unicode[STIX]{x1D71B}^{-\operatorname{val}_{F}(\unicode[STIX]{x1D702})})\operatorname{sgn}_{CD}(w^{\prime })\operatorname{sgn}_{CD}(w^{\prime \prime }))^{(R-r)/2}\nonumber\\ \displaystyle & & \displaystyle \qquad \times \,\left(\displaystyle \mathop{\prod }_{j\in {\hat{J}}}\operatorname{sgn}(\unicode[STIX]{x1D6FE}_{j-1}\unicode[STIX]{x1D6FE}_{j})^{j/2-1}\operatorname{sgn}(\unicode[STIX]{x1D6FE}_{j-1}-\unicode[STIX]{x1D6FE}_{j})\right)\nonumber\\ \displaystyle & & \displaystyle \qquad \times \,\left(\displaystyle \mathop{\prod }_{j=R-r+1,\ldots ,R}\operatorname{sgn}(\unicode[STIX]{x1D6FE}_{j})^{(R-r)/2}\right)\nonumber\\ \displaystyle & & \displaystyle \qquad \times \,\operatorname{sgn}(-1)^{\operatorname{val}_{F}(\unicode[STIX]{x1D702}[L_{2},\unicode[STIX]{x1D6FE}])B}\operatorname{sgn}(\unicode[STIX]{x1D702}[L_{2},\unicode[STIX]{x1D6FE}]\unicode[STIX]{x1D71B}^{-\operatorname{val}_{F}(\unicode[STIX]{x1D702}[L_{2},\unicode[STIX]{x1D6FE}])})^{B}\operatorname{sgn}_{CD}(w^{\prime \prime })^{B}.\end{eqnarray}$$
Le lemme résulte de (1), (2) et (4). ◻
2.7 Démonstration du (ii) du lemme 2.2
Soit
![]() $(\bar{n}_{1},\bar{n}_{2})\in D(n)$
et
$(\bar{n}_{1},\bar{n}_{2})\in D(n)$
et
![]() $\unicode[STIX]{x1D702}_{1},\unicode[STIX]{x1D702}_{2}\in F^{\times }/F^{\times 2}$
tels que
$\unicode[STIX]{x1D702}_{1},\unicode[STIX]{x1D702}_{2}\in F^{\times }/F^{\times 2}$
tels que
![]() $\unicode[STIX]{x1D702}_{1}\unicode[STIX]{x1D702}_{2}=\unicode[STIX]{x1D702}$
. Soit
$\unicode[STIX]{x1D702}_{1}\unicode[STIX]{x1D702}_{2}=\unicode[STIX]{x1D702}$
. Soit
![]() $\bar{Y}_{1}$
, respectivement
$\bar{Y}_{1}$
, respectivement
![]() $\bar{Y}_{2}$
, un élément régulier, elliptique et topologiquement nilpotent de
$\bar{Y}_{2}$
, un élément régulier, elliptique et topologiquement nilpotent de
![]() $\mathfrak{g}_{\bar{n}_{1},\unicode[STIX]{x1D702}_{1}}(F)$
, respectivement
$\mathfrak{g}_{\bar{n}_{1},\unicode[STIX]{x1D702}_{1}}(F)$
, respectivement
![]() $\mathfrak{g}_{\bar{n}_{2},\unicode[STIX]{x1D702}_{2}}(F)$
. On va calculer l’intégrale orbitale endoscopique
$\mathfrak{g}_{\bar{n}_{2},\unicode[STIX]{x1D702}_{2}}(F)$
. On va calculer l’intégrale orbitale endoscopique
![]() $J^{\operatorname{endo}}(\bar{Y}_{1},\bar{Y}_{2},f)$
, cf. 1.2 dont les définitions s’adaptent aux algèbres de Lie.
$J^{\operatorname{endo}}(\bar{Y}_{1},\bar{Y}_{2},f)$
, cf. 1.2 dont les définitions s’adaptent aux algèbres de Lie.
Soit
![]() $\sharp =\operatorname{iso}$
ou
$\sharp =\operatorname{iso}$
ou
![]() $\operatorname{an}$
. Pour
$\operatorname{an}$
. Pour
![]() $(L_{1},L_{2})\in {\mathcal{L}}$
,
$(L_{1},L_{2})\in {\mathcal{L}}$
,
![]() $\unicode[STIX]{x1D6FE}\in \unicode[STIX]{x1D6E4}$
et
$\unicode[STIX]{x1D6FE}\in \unicode[STIX]{x1D6E4}$
et
![]() $a\in A(\unicode[STIX]{x1D6FE})$
, posons
$a\in A(\unicode[STIX]{x1D6FE})$
, posons
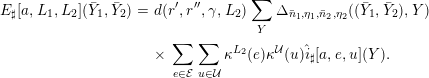 $$\begin{eqnarray}\displaystyle E_{\sharp }[a,L_{1},L_{2}](\bar{Y}_{1},\bar{Y}_{2}) & = & \displaystyle d(r^{\prime },r^{\prime \prime },\unicode[STIX]{x1D6FE},L_{2})\mathop{\sum }_{Y}\unicode[STIX]{x1D6E5}_{\bar{n}_{1},\unicode[STIX]{x1D702}_{1},\bar{n}_{2},\unicode[STIX]{x1D702}_{2}}((\bar{Y}_{1},\bar{Y}_{2}),Y)\nonumber\\ \displaystyle & & \displaystyle \times \,\mathop{\sum }_{e\in {\mathcal{E}}}\mathop{\sum }_{u\in {\mathcal{U}}}\unicode[STIX]{x1D705}^{L_{2}}(e)\unicode[STIX]{x1D705}^{{\mathcal{U}}}(u)\hat{i} _{\sharp }[a,e,u](Y).\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle E_{\sharp }[a,L_{1},L_{2}](\bar{Y}_{1},\bar{Y}_{2}) & = & \displaystyle d(r^{\prime },r^{\prime \prime },\unicode[STIX]{x1D6FE},L_{2})\mathop{\sum }_{Y}\unicode[STIX]{x1D6E5}_{\bar{n}_{1},\unicode[STIX]{x1D702}_{1},\bar{n}_{2},\unicode[STIX]{x1D702}_{2}}((\bar{Y}_{1},\bar{Y}_{2}),Y)\nonumber\\ \displaystyle & & \displaystyle \times \,\mathop{\sum }_{e\in {\mathcal{E}}}\mathop{\sum }_{u\in {\mathcal{U}}}\unicode[STIX]{x1D705}^{L_{2}}(e)\unicode[STIX]{x1D705}^{{\mathcal{U}}}(u)\hat{i} _{\sharp }[a,e,u](Y).\end{eqnarray}$$
En utilisant le lemme 2.5, on calcule
où l’on a posé
Par définition, on a l’égalité
D’où l’égalité
où l’on a posé
Fixons
![]() $\sharp =\operatorname{iso}$
ou
$\sharp =\operatorname{iso}$
ou
![]() $\operatorname{an}$
,
$\operatorname{an}$
,
![]() $(L_{1},L_{2})\in {\mathcal{L}}$
,
$(L_{1},L_{2})\in {\mathcal{L}}$
,
![]() $\unicode[STIX]{x1D6FE}\in \unicode[STIX]{x1D6E4}$
et
$\unicode[STIX]{x1D6FE}\in \unicode[STIX]{x1D6E4}$
et
![]() $a\in A(\unicode[STIX]{x1D6FE})$
. Rappelons que, pour
$a\in A(\unicode[STIX]{x1D6FE})$
. Rappelons que, pour
![]() $e\in {\mathcal{E}}$
et
$e\in {\mathcal{E}}$
et
![]() $u\in {\mathcal{U}}$
, on a l’égalité
$u\in {\mathcal{U}}$
, on a l’égalité
![]() $\hat{i} _{\sharp }[a,e,u]=\frac{1}{2}(\hat{i} _{\sharp }^{+}[a,e,u]+\hat{i} _{\sharp }^{-}[a,e,u])$
. Supposons que
$\hat{i} _{\sharp }[a,e,u]=\frac{1}{2}(\hat{i} _{\sharp }^{+}[a,e,u]+\hat{i} _{\sharp }^{-}[a,e,u])$
. Supposons que
![]() $n_{1}\not =0$
et
$n_{1}\not =0$
et
![]() $n_{2}\not =0$
. On a défini en 2.6 une application qui, à
$n_{2}\not =0$
. On a défini en 2.6 une application qui, à
![]() $\unicode[STIX]{x1D701}_{1},\unicode[STIX]{x1D701}_{2}=\pm$
, associe
$\unicode[STIX]{x1D701}_{1},\unicode[STIX]{x1D701}_{2}=\pm$
, associe
![]() $\unicode[STIX]{x1D701}=\pm$
de sorte que les classes de conjugaison stable de
$\unicode[STIX]{x1D701}=\pm$
de sorte que les classes de conjugaison stable de
![]() $(X^{\unicode[STIX]{x1D701}_{1}}(a^{L_{1}},w^{\prime \prime }),X^{\unicode[STIX]{x1D701}_{2}}(a^{L_{2}},w^{\prime \prime }))$
et
$(X^{\unicode[STIX]{x1D701}_{1}}(a^{L_{1}},w^{\prime \prime }),X^{\unicode[STIX]{x1D701}_{2}}(a^{L_{2}},w^{\prime \prime }))$
et
![]() $X^{\unicode[STIX]{x1D701}}(a,e,u)$
se correspondent. Notons-la
$X^{\unicode[STIX]{x1D701}}(a,e,u)$
se correspondent. Notons-la
![]() $Z$
. Elle est surjective et ses fibres ont deux éléments. On a donc
$Z$
. Elle est surjective et ses fibres ont deux éléments. On a donc
Utilisons le lemme 2.6. Alors
 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D705}^{L_{2}}(e)\unicode[STIX]{x1D705}^{{\mathcal{U}}}(u)\hat{i} _{\sharp }[a,e,u] & = & \displaystyle \frac{1}{4}\mathop{\sum }_{\unicode[STIX]{x1D701}_{1},\unicode[STIX]{x1D701}_{2}=\pm }d(r^{\prime },r^{\prime \prime },\unicode[STIX]{x1D6FE},L_{2})\nonumber\\ \displaystyle & & \displaystyle \times \,\unicode[STIX]{x1D6E5}_{n_{1},\unicode[STIX]{x1D702}[L_{1},\unicode[STIX]{x1D6FE}],n_{2},\unicode[STIX]{x1D702}[L_{2},\unicode[STIX]{x1D6FE}]} (\,(X^{\unicode[STIX]{x1D701}_{1}}(a^{L_{1}},w^{\prime }),X^{\unicode[STIX]{x1D701}_{2}}(a^{L_{2}},w^{\prime \prime })),\nonumber\\ \displaystyle & & \displaystyle X^{Z(\unicode[STIX]{x1D701}_{1},\unicode[STIX]{x1D701}_{2})}(a,e,u))\hat{i} _{\sharp }^{Z(\unicode[STIX]{x1D701}_{1},\unicode[STIX]{x1D701}_{2})}[a,e,u].\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D705}^{L_{2}}(e)\unicode[STIX]{x1D705}^{{\mathcal{U}}}(u)\hat{i} _{\sharp }[a,e,u] & = & \displaystyle \frac{1}{4}\mathop{\sum }_{\unicode[STIX]{x1D701}_{1},\unicode[STIX]{x1D701}_{2}=\pm }d(r^{\prime },r^{\prime \prime },\unicode[STIX]{x1D6FE},L_{2})\nonumber\\ \displaystyle & & \displaystyle \times \,\unicode[STIX]{x1D6E5}_{n_{1},\unicode[STIX]{x1D702}[L_{1},\unicode[STIX]{x1D6FE}],n_{2},\unicode[STIX]{x1D702}[L_{2},\unicode[STIX]{x1D6FE}]} (\,(X^{\unicode[STIX]{x1D701}_{1}}(a^{L_{1}},w^{\prime }),X^{\unicode[STIX]{x1D701}_{2}}(a^{L_{2}},w^{\prime \prime })),\nonumber\\ \displaystyle & & \displaystyle X^{Z(\unicode[STIX]{x1D701}_{1},\unicode[STIX]{x1D701}_{2})}(a,e,u))\hat{i} _{\sharp }^{Z(\unicode[STIX]{x1D701}_{1},\unicode[STIX]{x1D701}_{2})}[a,e,u].\nonumber\end{eqnarray}$$
L’égalité (1) se récrit
 $$\begin{eqnarray}\displaystyle & & \displaystyle E_{\sharp }[a,L_{1},L_{2}](\bar{Y}_{1},\bar{Y}_{2})\nonumber\\ \displaystyle & & \displaystyle \quad =\frac{1}{4}\mathop{\sum }_{\unicode[STIX]{x1D701}_{1},\unicode[STIX]{x1D701}_{2}=\pm }\mathop{\sum }_{Y}\unicode[STIX]{x1D6E5}_{\bar{n}_{1},\unicode[STIX]{x1D702}_{1},\bar{n}_{2},\unicode[STIX]{x1D702}_{2}}((\bar{Y}_{1},\bar{Y}_{2}),Y)E_{\sharp }^{\unicode[STIX]{x1D701}_{1},\unicode[STIX]{x1D701}_{2}}[a,L_{1},L_{2}](Y),\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle E_{\sharp }[a,L_{1},L_{2}](\bar{Y}_{1},\bar{Y}_{2})\nonumber\\ \displaystyle & & \displaystyle \quad =\frac{1}{4}\mathop{\sum }_{\unicode[STIX]{x1D701}_{1},\unicode[STIX]{x1D701}_{2}=\pm }\mathop{\sum }_{Y}\unicode[STIX]{x1D6E5}_{\bar{n}_{1},\unicode[STIX]{x1D702}_{1},\bar{n}_{2},\unicode[STIX]{x1D702}_{2}}((\bar{Y}_{1},\bar{Y}_{2}),Y)E_{\sharp }^{\unicode[STIX]{x1D701}_{1},\unicode[STIX]{x1D701}_{2}}[a,L_{1},L_{2}](Y),\end{eqnarray}$$
où
 $$\begin{eqnarray}\displaystyle & & \displaystyle E_{\sharp }^{\unicode[STIX]{x1D701}_{1},\unicode[STIX]{x1D701}_{2}}[a,L_{1},L_{2}](Y)\nonumber\\ \displaystyle & & \displaystyle \quad =\mathop{\sum }_{e\in {\mathcal{E}}}\mathop{\sum }_{u\in {\mathcal{U}}}\unicode[STIX]{x1D6E5}_{n_{1},\unicode[STIX]{x1D702}[L_{1},\unicode[STIX]{x1D6FE}],n_{2},\unicode[STIX]{x1D702}[L_{2},\unicode[STIX]{x1D6FE}]} (\,(X^{\unicode[STIX]{x1D701}_{1}}(a^{L_{1}},w^{\prime }),X^{\unicode[STIX]{x1D701}_{2}}(a^{L_{2}},w^{\prime \prime })),\nonumber\\ \displaystyle & & \displaystyle \qquad X^{Z(\unicode[STIX]{x1D701}_{1},\unicode[STIX]{x1D701}_{2})}(a,e,u))\hat{i} _{\sharp }^{Z(\unicode[STIX]{x1D701}_{1},\unicode[STIX]{x1D701}_{2})}[a,e,u](Y).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle E_{\sharp }^{\unicode[STIX]{x1D701}_{1},\unicode[STIX]{x1D701}_{2}}[a,L_{1},L_{2}](Y)\nonumber\\ \displaystyle & & \displaystyle \quad =\mathop{\sum }_{e\in {\mathcal{E}}}\mathop{\sum }_{u\in {\mathcal{U}}}\unicode[STIX]{x1D6E5}_{n_{1},\unicode[STIX]{x1D702}[L_{1},\unicode[STIX]{x1D6FE}],n_{2},\unicode[STIX]{x1D702}[L_{2},\unicode[STIX]{x1D6FE}]} (\,(X^{\unicode[STIX]{x1D701}_{1}}(a^{L_{1}},w^{\prime }),X^{\unicode[STIX]{x1D701}_{2}}(a^{L_{2}},w^{\prime \prime })),\nonumber\\ \displaystyle & & \displaystyle \qquad X^{Z(\unicode[STIX]{x1D701}_{1},\unicode[STIX]{x1D701}_{2})}(a,e,u))\hat{i} _{\sharp }^{Z(\unicode[STIX]{x1D701}_{1},\unicode[STIX]{x1D701}_{2})}[a,e,u](Y).\nonumber\end{eqnarray}$$
Fixons
![]() $\unicode[STIX]{x1D701}_{1}$
et
$\unicode[STIX]{x1D701}_{1}$
et
![]() $\unicode[STIX]{x1D701}_{2}$
. Dans la formule définissant
$\unicode[STIX]{x1D701}_{2}$
. Dans la formule définissant
![]() $E_{\sharp }^{\unicode[STIX]{x1D701}_{1},\unicode[STIX]{x1D701}_{2}}[a,L_{1},L_{2}](Y)$
, la somme est en réalité limitée aux
$E_{\sharp }^{\unicode[STIX]{x1D701}_{1},\unicode[STIX]{x1D701}_{2}}[a,L_{1},L_{2}](Y)$
, la somme est en réalité limitée aux
![]() $(e,u)$
tels que
$(e,u)$
tels que
![]() $\sharp (a,e,u)=\sharp$
(pour les autres,
$\sharp (a,e,u)=\sharp$
(pour les autres,
![]() $\hat{i} _{\sharp }^{Z(\unicode[STIX]{x1D701}_{1},\unicode[STIX]{x1D701}_{2})}[a,e,u]$
est nulle). Les
$\hat{i} _{\sharp }^{Z(\unicode[STIX]{x1D701}_{1},\unicode[STIX]{x1D701}_{2})}[a,e,u]$
est nulle). Les
![]() $X^{Z(\unicode[STIX]{x1D701}_{1},\unicode[STIX]{x1D701}_{2})}(a,e,u)$
parcourent un ensemble de représentants des classes de conjugaison par
$X^{Z(\unicode[STIX]{x1D701}_{1},\unicode[STIX]{x1D701}_{2})}(a,e,u)$
parcourent un ensemble de représentants des classes de conjugaison par
![]() $G_{\sharp }(F)$
dans la classe de conjugaison stable correspondant à celle de
$G_{\sharp }(F)$
dans la classe de conjugaison stable correspondant à celle de
![]() $(X^{\unicode[STIX]{x1D701}_{1}}(a^{L_{1}},w^{\prime }),X^{\unicode[STIX]{x1D701}_{2}}(a^{L_{2}},w^{\prime \prime }))$
. On voit qu’aux différences de notations et à une constante près,
$(X^{\unicode[STIX]{x1D701}_{1}}(a^{L_{1}},w^{\prime }),X^{\unicode[STIX]{x1D701}_{2}}(a^{L_{2}},w^{\prime \prime }))$
. On voit qu’aux différences de notations et à une constante près,
![]() $E_{\sharp }^{\unicode[STIX]{x1D701}_{1},\unicode[STIX]{x1D701}_{2}}[a,L_{1},L_{2}](Y)$
n’est autre que le membre de droite de l’égalité de la conjecture 2 de [Reference Waldspurger10] VIII.7. Cette conjecture est démontrée depuis que Ngo Bao Chau a démontré le lemme fondamental. On va appliquer cette conjecture. Posons
$E_{\sharp }^{\unicode[STIX]{x1D701}_{1},\unicode[STIX]{x1D701}_{2}}[a,L_{1},L_{2}](Y)$
n’est autre que le membre de droite de l’égalité de la conjecture 2 de [Reference Waldspurger10] VIII.7. Cette conjecture est démontrée depuis que Ngo Bao Chau a démontré le lemme fondamental. On va appliquer cette conjecture. Posons
avec les définitions de [Reference Waldspurger10] VIII.5. Pour
![]() $j=1,2$
et pour un élément régulier
$j=1,2$
et pour un élément régulier
![]() $Y_{j}$
de
$Y_{j}$
de
![]() $\mathfrak{g}_{n_{j},\unicode[STIX]{x1D702}[L_{j},\unicode[STIX]{x1D6FE}],\operatorname{iso}}(F)$
, notons
$\mathfrak{g}_{n_{j},\unicode[STIX]{x1D702}[L_{j},\unicode[STIX]{x1D6FE}],\operatorname{iso}}(F)$
, notons
![]() $z_{\operatorname{iso}}(Y_{j})$
le nombre de classes de conjugaison par
$z_{\operatorname{iso}}(Y_{j})$
le nombre de classes de conjugaison par
![]() $G_{n_{j},\unicode[STIX]{x1D702}[L_{j},\unicode[STIX]{x1D6FE}],\operatorname{iso}}(F)$
dans la classe de conjugaison stable de
$G_{n_{j},\unicode[STIX]{x1D702}[L_{j},\unicode[STIX]{x1D6FE}],\operatorname{iso}}(F)$
dans la classe de conjugaison stable de
![]() $Y_{j}$
. Rappelons que
$Y_{j}$
. Rappelons que
![]() $X^{\unicode[STIX]{x1D701}_{1}}(a^{L_{1}},w^{\prime })$
est un élément d’une certaine classe de conjugaison stable, cf. 2.6. Un ensemble de classes de conjugaison par
$X^{\unicode[STIX]{x1D701}_{1}}(a^{L_{1}},w^{\prime })$
est un élément d’une certaine classe de conjugaison stable, cf. 2.6. Un ensemble de classes de conjugaison par
![]() $G_{n_{1},\unicode[STIX]{x1D702}[L_{1},\unicode[STIX]{x1D6FE}],\operatorname{iso}}(F)$
dans cette classe de conjugaison stable est formé d’éléments
$G_{n_{1},\unicode[STIX]{x1D702}[L_{1},\unicode[STIX]{x1D6FE}],\operatorname{iso}}(F)$
dans cette classe de conjugaison stable est formé d’éléments
![]() $X^{\unicode[STIX]{x1D701}_{1}}(a^{L_{1}},e_{1},u_{1})$
, où
$X^{\unicode[STIX]{x1D701}_{1}}(a^{L_{1}},e_{1},u_{1})$
, où
![]() $e_{1}$
et
$e_{1}$
et
![]() $u_{1}$
décrivent des ensembles
$u_{1}$
décrivent des ensembles
![]() ${\mathcal{E}}_{1}$
et
${\mathcal{E}}_{1}$
et
![]() ${\mathcal{U}}_{1}$
analogues à
${\mathcal{U}}_{1}$
analogues à
![]() ${\mathcal{E}}$
et
${\mathcal{E}}$
et
![]() ${\mathcal{U}}$
, avec la restriction
${\mathcal{U}}$
, avec la restriction
![]() $\sharp (a^{L_{1}},e_{1},u_{1})=\operatorname{iso}$
. On définit pour ces éléments une fonction
$\sharp (a^{L_{1}},e_{1},u_{1})=\operatorname{iso}$
. On définit pour ces éléments une fonction
![]() $\hat{i} _{\operatorname{iso}}^{\unicode[STIX]{x1D701}_{1}}[a^{L_{1}},e_{1},u_{1}]$
similaire à
$\hat{i} _{\operatorname{iso}}^{\unicode[STIX]{x1D701}_{1}}[a^{L_{1}},e_{1},u_{1}]$
similaire à
![]() $\hat{i} _{\sharp }^{\unicode[STIX]{x1D701}}[a,e,u]$
. Si la condition
$\hat{i} _{\sharp }^{\unicode[STIX]{x1D701}}[a,e,u]$
. Si la condition
![]() $\sharp (a^{L_{1}},e_{1},u_{1})=\operatorname{iso}$
n’est pas vérifiée, on pose
$\sharp (a^{L_{1}},e_{1},u_{1})=\operatorname{iso}$
n’est pas vérifiée, on pose
![]() $\hat{i} _{\operatorname{iso}}^{\unicode[STIX]{x1D701}_{1}}[a^{L_{1}},e_{1},u_{1}]=0$
. On pose des définitions analogues en remplaçant l’indice
$\hat{i} _{\operatorname{iso}}^{\unicode[STIX]{x1D701}_{1}}[a^{L_{1}},e_{1},u_{1}]=0$
. On pose des définitions analogues en remplaçant l’indice
![]() $1$
par
$1$
par
![]() $2$
(et
$2$
(et
![]() $w^{\prime }$
par
$w^{\prime }$
par
![]() $w^{\prime \prime }$
). Alors la conjecture 2 de [Reference Waldspurger10] VIII.7 fournit l’égalité
$w^{\prime \prime }$
). Alors la conjecture 2 de [Reference Waldspurger10] VIII.7 fournit l’égalité
 $$\begin{eqnarray}\displaystyle E_{\sharp }^{\unicode[STIX]{x1D701}_{1},\unicode[STIX]{x1D701}_{2}}[a,L_{1},L_{2}](Y) & = & \displaystyle C_{\sharp }(n_{1},\unicode[STIX]{x1D702}[L_{1},\unicode[STIX]{x1D6FE}],n_{2},\unicode[STIX]{x1D702}[L_{2},\unicode[STIX]{x1D6FE}])\nonumber\\ \displaystyle & & \displaystyle \times \,\mathop{\sum }_{e_{1}\in {\mathcal{E}}_{1},u_{1}\in {\mathcal{U}}_{1},e_{2}\in {\mathcal{E}}_{2},u_{2}\in {\mathcal{U}}_{2}}\mathop{\sum }_{Y_{1},Y_{2}}z_{\operatorname{iso}}(Y_{1})^{-1}z_{\operatorname{iso}}(Y_{2})^{-1}\nonumber\\ \displaystyle & & \displaystyle \times \,\unicode[STIX]{x1D6E5}_{n_{1},\unicode[STIX]{x1D702}[L_{1},\unicode[STIX]{x1D6FE}],n_{2},\unicode[STIX]{x1D702}[L_{2},\unicode[STIX]{x1D6FE}]}((Y_{1},Y_{2}),Y)\hat{i} _{\operatorname{iso}}^{\unicode[STIX]{x1D701}_{1}}[a^{L_{1}},e_{1},u_{1}]\nonumber\\ \displaystyle & & \displaystyle \times \,(Y_{1})\hat{i} _{\operatorname{iso}}^{\unicode[STIX]{x1D701}_{2}}[a^{L_{2}},e_{2},u_{2}](Y_{2}),\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle E_{\sharp }^{\unicode[STIX]{x1D701}_{1},\unicode[STIX]{x1D701}_{2}}[a,L_{1},L_{2}](Y) & = & \displaystyle C_{\sharp }(n_{1},\unicode[STIX]{x1D702}[L_{1},\unicode[STIX]{x1D6FE}],n_{2},\unicode[STIX]{x1D702}[L_{2},\unicode[STIX]{x1D6FE}])\nonumber\\ \displaystyle & & \displaystyle \times \,\mathop{\sum }_{e_{1}\in {\mathcal{E}}_{1},u_{1}\in {\mathcal{U}}_{1},e_{2}\in {\mathcal{E}}_{2},u_{2}\in {\mathcal{U}}_{2}}\mathop{\sum }_{Y_{1},Y_{2}}z_{\operatorname{iso}}(Y_{1})^{-1}z_{\operatorname{iso}}(Y_{2})^{-1}\nonumber\\ \displaystyle & & \displaystyle \times \,\unicode[STIX]{x1D6E5}_{n_{1},\unicode[STIX]{x1D702}[L_{1},\unicode[STIX]{x1D6FE}],n_{2},\unicode[STIX]{x1D702}[L_{2},\unicode[STIX]{x1D6FE}]}((Y_{1},Y_{2}),Y)\hat{i} _{\operatorname{iso}}^{\unicode[STIX]{x1D701}_{1}}[a^{L_{1}},e_{1},u_{1}]\nonumber\\ \displaystyle & & \displaystyle \times \,(Y_{1})\hat{i} _{\operatorname{iso}}^{\unicode[STIX]{x1D701}_{2}}[a^{L_{2}},e_{2},u_{2}](Y_{2}),\end{eqnarray}$$
où l’on somme sur les
![]() $(Y_{1},Y_{2})$
, elliptiques réguliers dans
$(Y_{1},Y_{2})$
, elliptiques réguliers dans
![]() $\mathfrak{g}_{n_{1},\unicode[STIX]{x1D702}[L_{1},\unicode[STIX]{x1D6FE}],\operatorname{iso}}(F)\times \mathfrak{g}_{n_{2},\unicode[STIX]{x1D702}[L_{2},\unicode[STIX]{x1D6FE}],\operatorname{iso}}(F)$
, à conjugaison près par
$\mathfrak{g}_{n_{1},\unicode[STIX]{x1D702}[L_{1},\unicode[STIX]{x1D6FE}],\operatorname{iso}}(F)\times \mathfrak{g}_{n_{2},\unicode[STIX]{x1D702}[L_{2},\unicode[STIX]{x1D6FE}],\operatorname{iso}}(F)$
, à conjugaison près par
![]() $G_{n_{1},\unicode[STIX]{x1D702}[L_{1},\unicode[STIX]{x1D6FE}],\operatorname{iso}}(F)\times G_{n_{2},\unicode[STIX]{x1D702}[L_{2},\unicode[STIX]{x1D6FE}],\operatorname{iso}}(F)$
.
$G_{n_{1},\unicode[STIX]{x1D702}[L_{1},\unicode[STIX]{x1D6FE}],\operatorname{iso}}(F)\times G_{n_{2},\unicode[STIX]{x1D702}[L_{2},\unicode[STIX]{x1D6FE}],\operatorname{iso}}(F)$
.
Calculons
![]() $C_{\sharp }(n_{1},\unicode[STIX]{x1D702}[L_{1},\unicode[STIX]{x1D6FE}],n_{2},\unicode[STIX]{x1D702}[L_{2},\unicode[STIX]{x1D6FE}])$
. D’après [Reference Moeglin and Waldspurger6] 3.15, on a les égalités
$C_{\sharp }(n_{1},\unicode[STIX]{x1D702}[L_{1},\unicode[STIX]{x1D6FE}],n_{2},\unicode[STIX]{x1D702}[L_{2},\unicode[STIX]{x1D6FE}])$
. D’après [Reference Moeglin and Waldspurger6] 3.15, on a les égalités
![]() $\unicode[STIX]{x1D6FE}_{\unicode[STIX]{x1D713}_{F}}(\mathfrak{g}_{\sharp }(F))=\unicode[STIX]{x1D6FE}_{\unicode[STIX]{x1D713}_{F}}^{n}\operatorname{sgn}(\unicode[STIX]{x1D702}\unicode[STIX]{x1D71B}^{-\operatorname{val}_{F}(\unicode[STIX]{x1D702})})$
, si
$\unicode[STIX]{x1D6FE}_{\unicode[STIX]{x1D713}_{F}}(\mathfrak{g}_{\sharp }(F))=\unicode[STIX]{x1D6FE}_{\unicode[STIX]{x1D713}_{F}}^{n}\operatorname{sgn}(\unicode[STIX]{x1D702}\unicode[STIX]{x1D71B}^{-\operatorname{val}_{F}(\unicode[STIX]{x1D702})})$
, si
![]() $\operatorname{val}_{F}(\unicode[STIX]{x1D702})$
est pair ;
$\operatorname{val}_{F}(\unicode[STIX]{x1D702})$
est pair ;
![]() $\unicode[STIX]{x1D6FE}_{\unicode[STIX]{x1D713}_{F}}(\mathfrak{g}_{\sharp }(F))=\unicode[STIX]{x1D6FE}_{\unicode[STIX]{x1D713}_{F}}^{n-1}$
si
$\unicode[STIX]{x1D6FE}_{\unicode[STIX]{x1D713}_{F}}(\mathfrak{g}_{\sharp }(F))=\unicode[STIX]{x1D6FE}_{\unicode[STIX]{x1D713}_{F}}^{n-1}$
si
![]() $\operatorname{val}_{F}(\unicode[STIX]{x1D702})$
est impair.
$\operatorname{val}_{F}(\unicode[STIX]{x1D702})$
est impair.
Le terme
![]() $\unicode[STIX]{x1D6FE}_{\unicode[STIX]{x1D713}_{F}}$
est une constante de Weil élémentaire. Il vérifie l’égalité
$\unicode[STIX]{x1D6FE}_{\unicode[STIX]{x1D713}_{F}}$
est une constante de Weil élémentaire. Il vérifie l’égalité
![]() $\unicode[STIX]{x1D6FE}_{\unicode[STIX]{x1D713}_{F}}^{2}=\operatorname{sgn}(-1)$
. On voit tout d’abord que les termes ci-dessus ne dépendent pas de l’indice
$\unicode[STIX]{x1D6FE}_{\unicode[STIX]{x1D713}_{F}}^{2}=\operatorname{sgn}(-1)$
. On voit tout d’abord que les termes ci-dessus ne dépendent pas de l’indice
![]() $\sharp$
. La constante
$\sharp$
. La constante
![]() $C_{\sharp }(n_{1},\unicode[STIX]{x1D702}[L_{1},\unicode[STIX]{x1D6FE}],n_{2},\unicode[STIX]{x1D702}[L_{2},\unicode[STIX]{x1D6FE}])$
non plus, on la note simplement
$C_{\sharp }(n_{1},\unicode[STIX]{x1D702}[L_{1},\unicode[STIX]{x1D6FE}],n_{2},\unicode[STIX]{x1D702}[L_{2},\unicode[STIX]{x1D6FE}])$
non plus, on la note simplement
![]() $C(n_{1},\unicode[STIX]{x1D702}[L_{1},\unicode[STIX]{x1D6FE}],n_{2},\unicode[STIX]{x1D702}[L_{2},\unicode[STIX]{x1D6FE}])$
. Pour
$C(n_{1},\unicode[STIX]{x1D702}[L_{1},\unicode[STIX]{x1D6FE}],n_{2},\unicode[STIX]{x1D702}[L_{2},\unicode[STIX]{x1D6FE}])$
. Pour
![]() $j=1,2$
, on a des formules analogues pour
$j=1,2$
, on a des formules analogues pour
![]() $\unicode[STIX]{x1D6FE}_{\unicode[STIX]{x1D713}_{F}}(\mathfrak{g}_{n_{j},\unicode[STIX]{x1D702}[L_{j},\unicode[STIX]{x1D6FE}],\operatorname{iso}}(F))$
. On obtient les égalités
$\unicode[STIX]{x1D6FE}_{\unicode[STIX]{x1D713}_{F}}(\mathfrak{g}_{n_{j},\unicode[STIX]{x1D702}[L_{j},\unicode[STIX]{x1D6FE}],\operatorname{iso}}(F))$
. On obtient les égalités
 $$\begin{eqnarray}\displaystyle & & \displaystyle C(n_{1},\unicode[STIX]{x1D702}[L_{1},\unicode[STIX]{x1D6FE}],n_{2},\unicode[STIX]{x1D702}[L_{2},\unicode[STIX]{x1D6FE}])\nonumber\\ \displaystyle & & \displaystyle \quad =\left\{\begin{array}{@{}ll@{}}1, & \text{pour}\,~\operatorname{val}_{F}(\unicode[STIX]{x1D702}[L_{1},\unicode[STIX]{x1D6FE}])\,\,\operatorname{pair}\\ & \text{et}\,\,\operatorname{val}_{F}(\unicode[STIX]{x1D702}[L_{2},\unicode[STIX]{x1D6FE}])\,\,\operatorname{pair}\,;\\ \operatorname{sgn}(\unicode[STIX]{x1D702}[L_{1},\unicode[STIX]{x1D6FE}]\unicode[STIX]{x1D71B}^{-\operatorname{val}_{F}(\unicode[STIX]{x1D702}[L_{1},\unicode[STIX]{x1D6FE}])}), & \text{pour}\,~\operatorname{val}_{F}(\unicode[STIX]{x1D702}[L_{1},\unicode[STIX]{x1D6FE}])\,\,\operatorname{pair}\\ & \text{et}\,\,\operatorname{val}_{F}(\unicode[STIX]{x1D702}[L_{2},\unicode[STIX]{x1D6FE}])\,\,\operatorname{impair}\,;\\ \operatorname{sgn}(\unicode[STIX]{x1D702}[L_{2},\unicode[STIX]{x1D6FE}]\unicode[STIX]{x1D71B}^{-\operatorname{val}_{F}(\unicode[STIX]{x1D702}[L_{2},\unicode[STIX]{x1D6FE}])}), & \text{pour}\,~\operatorname{val}_{F}(\unicode[STIX]{x1D702}[L_{1},\unicode[STIX]{x1D6FE}])\,\,\operatorname{impair}\\ & \text{et}\,\,\operatorname{val}_{F}(\unicode[STIX]{x1D702}[L_{2},\unicode[STIX]{x1D6FE}])\,\,\operatorname{pair}\,;\\ \operatorname{sgn}(-\unicode[STIX]{x1D702}\unicode[STIX]{x1D71B}^{-\operatorname{val}_{F}(\unicode[STIX]{x1D702})}), & \text{pour}\,~\operatorname{val}_{F}(\unicode[STIX]{x1D702}[L_{1},\unicode[STIX]{x1D6FE}])\,\,\operatorname{impair}\\ & \text{et}\,\,\operatorname{val}_{F}(\unicode[STIX]{x1D702}[L_{2},\unicode[STIX]{x1D6FE}])\,\,\operatorname{impair}\!.\end{array}\right.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle C(n_{1},\unicode[STIX]{x1D702}[L_{1},\unicode[STIX]{x1D6FE}],n_{2},\unicode[STIX]{x1D702}[L_{2},\unicode[STIX]{x1D6FE}])\nonumber\\ \displaystyle & & \displaystyle \quad =\left\{\begin{array}{@{}ll@{}}1, & \text{pour}\,~\operatorname{val}_{F}(\unicode[STIX]{x1D702}[L_{1},\unicode[STIX]{x1D6FE}])\,\,\operatorname{pair}\\ & \text{et}\,\,\operatorname{val}_{F}(\unicode[STIX]{x1D702}[L_{2},\unicode[STIX]{x1D6FE}])\,\,\operatorname{pair}\,;\\ \operatorname{sgn}(\unicode[STIX]{x1D702}[L_{1},\unicode[STIX]{x1D6FE}]\unicode[STIX]{x1D71B}^{-\operatorname{val}_{F}(\unicode[STIX]{x1D702}[L_{1},\unicode[STIX]{x1D6FE}])}), & \text{pour}\,~\operatorname{val}_{F}(\unicode[STIX]{x1D702}[L_{1},\unicode[STIX]{x1D6FE}])\,\,\operatorname{pair}\\ & \text{et}\,\,\operatorname{val}_{F}(\unicode[STIX]{x1D702}[L_{2},\unicode[STIX]{x1D6FE}])\,\,\operatorname{impair}\,;\\ \operatorname{sgn}(\unicode[STIX]{x1D702}[L_{2},\unicode[STIX]{x1D6FE}]\unicode[STIX]{x1D71B}^{-\operatorname{val}_{F}(\unicode[STIX]{x1D702}[L_{2},\unicode[STIX]{x1D6FE}])}), & \text{pour}\,~\operatorname{val}_{F}(\unicode[STIX]{x1D702}[L_{1},\unicode[STIX]{x1D6FE}])\,\,\operatorname{impair}\\ & \text{et}\,\,\operatorname{val}_{F}(\unicode[STIX]{x1D702}[L_{2},\unicode[STIX]{x1D6FE}])\,\,\operatorname{pair}\,;\\ \operatorname{sgn}(-\unicode[STIX]{x1D702}\unicode[STIX]{x1D71B}^{-\operatorname{val}_{F}(\unicode[STIX]{x1D702})}), & \text{pour}\,~\operatorname{val}_{F}(\unicode[STIX]{x1D702}[L_{1},\unicode[STIX]{x1D6FE}])\,\,\operatorname{impair}\\ & \text{et}\,\,\operatorname{val}_{F}(\unicode[STIX]{x1D702}[L_{2},\unicode[STIX]{x1D6FE}])\,\,\operatorname{impair}\!.\end{array}\right.\nonumber\end{eqnarray}$$
Insérons l’égalité (4) dans la formule (3). Pour
![]() $j=1,2$
, posons
$j=1,2$
, posons
On obtient
 $$\begin{eqnarray}\displaystyle E_{\sharp }[a,L_{1},L_{2}](\bar{Y}_{1},\bar{Y}_{2}) & = & \displaystyle C(n_{1},\unicode[STIX]{x1D702}[L_{1},\unicode[STIX]{x1D6FE}],n_{2},\unicode[STIX]{x1D702}[L_{2},\unicode[STIX]{x1D6FE}])\nonumber\\ \displaystyle & & \displaystyle \times \,\mathop{\sum }_{e_{1}\in {\mathcal{E}}_{1},u_{1}\in {\mathcal{U}}_{1},e_{2}\in {\mathcal{E}}_{2},u_{2}\in {\mathcal{U}}_{2}}\mathop{\sum }_{Y_{1},Y_{2}}z_{\operatorname{iso}}(Y_{1})^{-1}z_{\operatorname{iso}}(Y_{2})^{-1}\nonumber\\ \displaystyle & & \displaystyle \times \,S_{\sharp ,L_{1},L_{2},\unicode[STIX]{x1D6FE}}(\bar{Y}_{1},\bar{Y}_{2},Y_{1},Y_{2})\hat{i} _{\operatorname{iso}}[a^{L_{1}},e_{1},u_{1}](Y_{1})\nonumber\\ \displaystyle & & \displaystyle \times \,\hat{i} _{\operatorname{iso}}[a^{L_{2}},e_{2},u_{2}](Y_{2}),\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle E_{\sharp }[a,L_{1},L_{2}](\bar{Y}_{1},\bar{Y}_{2}) & = & \displaystyle C(n_{1},\unicode[STIX]{x1D702}[L_{1},\unicode[STIX]{x1D6FE}],n_{2},\unicode[STIX]{x1D702}[L_{2},\unicode[STIX]{x1D6FE}])\nonumber\\ \displaystyle & & \displaystyle \times \,\mathop{\sum }_{e_{1}\in {\mathcal{E}}_{1},u_{1}\in {\mathcal{U}}_{1},e_{2}\in {\mathcal{E}}_{2},u_{2}\in {\mathcal{U}}_{2}}\mathop{\sum }_{Y_{1},Y_{2}}z_{\operatorname{iso}}(Y_{1})^{-1}z_{\operatorname{iso}}(Y_{2})^{-1}\nonumber\\ \displaystyle & & \displaystyle \times \,S_{\sharp ,L_{1},L_{2},\unicode[STIX]{x1D6FE}}(\bar{Y}_{1},\bar{Y}_{2},Y_{1},Y_{2})\hat{i} _{\operatorname{iso}}[a^{L_{1}},e_{1},u_{1}](Y_{1})\nonumber\\ \displaystyle & & \displaystyle \times \,\hat{i} _{\operatorname{iso}}[a^{L_{2}},e_{2},u_{2}](Y_{2}),\nonumber\end{eqnarray}$$
où
 $$\begin{eqnarray}\displaystyle S_{\sharp ,L_{1},L_{2},\unicode[STIX]{x1D6FE}}(\bar{Y}_{1},\bar{Y}_{2},Y_{1},Y_{2}) & = & \displaystyle \mathop{\sum }_{Y}\unicode[STIX]{x1D6E5}_{\bar{n}_{1},\unicode[STIX]{x1D702}_{1},\bar{n}_{2},\unicode[STIX]{x1D702}_{2}}((\bar{Y}_{1},\bar{Y}_{2}),Y)\nonumber\\ \displaystyle & & \displaystyle \times \,\unicode[STIX]{x1D6E5}_{n_{1},\unicode[STIX]{x1D702}[L_{1},\unicode[STIX]{x1D6FE}],n_{2},\unicode[STIX]{x1D702}[L_{2},\unicode[STIX]{x1D6FE}]}((Y_{1},Y_{2}),Y).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle S_{\sharp ,L_{1},L_{2},\unicode[STIX]{x1D6FE}}(\bar{Y}_{1},\bar{Y}_{2},Y_{1},Y_{2}) & = & \displaystyle \mathop{\sum }_{Y}\unicode[STIX]{x1D6E5}_{\bar{n}_{1},\unicode[STIX]{x1D702}_{1},\bar{n}_{2},\unicode[STIX]{x1D702}_{2}}((\bar{Y}_{1},\bar{Y}_{2}),Y)\nonumber\\ \displaystyle & & \displaystyle \times \,\unicode[STIX]{x1D6E5}_{n_{1},\unicode[STIX]{x1D702}[L_{1},\unicode[STIX]{x1D6FE}],n_{2},\unicode[STIX]{x1D702}[L_{2},\unicode[STIX]{x1D6FE}]}((Y_{1},Y_{2}),Y).\nonumber\end{eqnarray}$$
Rappelons que
![]() $Y$
décrit ici les éléments elliptiques réguliers de
$Y$
décrit ici les éléments elliptiques réguliers de
![]() $\mathfrak{g}_{\sharp }(F)$
, à conjugaison près par
$\mathfrak{g}_{\sharp }(F)$
, à conjugaison près par
![]() $G_{\sharp }(F)$
. Puisque
$G_{\sharp }(F)$
. Puisque
![]() $E[a,L_{1},L_{2}](\bar{Y}_{1},\bar{Y}_{2})$
est la somme de
$E[a,L_{1},L_{2}](\bar{Y}_{1},\bar{Y}_{2})$
est la somme de
![]() $E_{\operatorname{iso}}[a,L_{1},L_{2}](\bar{Y}_{1},\bar{Y}_{2})$
et de
$E_{\operatorname{iso}}[a,L_{1},L_{2}](\bar{Y}_{1},\bar{Y}_{2})$
et de
![]() $E_{\operatorname{an}}[a,L_{1},L_{2}](\bar{Y}_{1},\bar{Y}_{2})$
, on a
$E_{\operatorname{an}}[a,L_{1},L_{2}](\bar{Y}_{1},\bar{Y}_{2})$
, on a
 $$\begin{eqnarray}\displaystyle E[a,L_{1},L_{2}](\bar{Y}_{1},\bar{Y}_{2}) & = & \displaystyle C(n_{1},\unicode[STIX]{x1D702}[L_{1},\unicode[STIX]{x1D6FE}],n_{2},\unicode[STIX]{x1D702}[L_{2},\unicode[STIX]{x1D6FE}])\nonumber\\ \displaystyle & & \displaystyle \times \,\mathop{\sum }_{e_{1}\in {\mathcal{E}}_{1},u_{1}\in {\mathcal{U}}_{1},e_{2}\in {\mathcal{E}}_{2},u_{2}\in {\mathcal{U}}_{2}}\mathop{\sum }_{Y_{1},Y_{2}}z_{\operatorname{iso}}(Y_{1})^{-1}\nonumber\\ \displaystyle & & \displaystyle \times \,z_{\operatorname{iso}}(Y_{2})^{-1}S_{L_{1},L_{2},\unicode[STIX]{x1D6FE}}(\bar{Y}_{1},\bar{Y}_{2},Y_{1},Y_{2})\nonumber\\ \displaystyle & & \displaystyle \times \,\hat{i} _{\operatorname{iso}}[a^{L_{1}},e_{1},u_{1}](Y_{1})\hat{i} _{\operatorname{iso}}[a^{L_{2}},e_{2},u_{2}](Y_{2}),\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle E[a,L_{1},L_{2}](\bar{Y}_{1},\bar{Y}_{2}) & = & \displaystyle C(n_{1},\unicode[STIX]{x1D702}[L_{1},\unicode[STIX]{x1D6FE}],n_{2},\unicode[STIX]{x1D702}[L_{2},\unicode[STIX]{x1D6FE}])\nonumber\\ \displaystyle & & \displaystyle \times \,\mathop{\sum }_{e_{1}\in {\mathcal{E}}_{1},u_{1}\in {\mathcal{U}}_{1},e_{2}\in {\mathcal{E}}_{2},u_{2}\in {\mathcal{U}}_{2}}\mathop{\sum }_{Y_{1},Y_{2}}z_{\operatorname{iso}}(Y_{1})^{-1}\nonumber\\ \displaystyle & & \displaystyle \times \,z_{\operatorname{iso}}(Y_{2})^{-1}S_{L_{1},L_{2},\unicode[STIX]{x1D6FE}}(\bar{Y}_{1},\bar{Y}_{2},Y_{1},Y_{2})\nonumber\\ \displaystyle & & \displaystyle \times \,\hat{i} _{\operatorname{iso}}[a^{L_{1}},e_{1},u_{1}](Y_{1})\hat{i} _{\operatorname{iso}}[a^{L_{2}},e_{2},u_{2}](Y_{2}),\end{eqnarray}$$
où
On a supposé que
![]() $n_{1}\not =0$
et
$n_{1}\not =0$
et
![]() $n_{2}\not =0$
. Supposons que ces conditions ne sont pas vérifiées, par exemple que
$n_{2}\not =0$
. Supposons que ces conditions ne sont pas vérifiées, par exemple que
![]() $n_{2}=0$
. On reprend le calcul. Les seules différences résident dans le fait que les termes indexés par
$n_{2}=0$
. On reprend le calcul. Les seules différences résident dans le fait que les termes indexés par
![]() $2$
doivent disparaître. En particulier les
$2$
doivent disparaître. En particulier les
![]() $\unicode[STIX]{x1D701}_{2}$
. Les
$\unicode[STIX]{x1D701}_{2}$
. Les
![]() $\frac{1}{4}$
figurant dans les calculs sont remplacés par des
$\frac{1}{4}$
figurant dans les calculs sont remplacés par des
![]() $\frac{1}{2}$
. On obtient encore la formule (5), dont on fait disparaître les termes indexés par
$\frac{1}{2}$
. On obtient encore la formule (5), dont on fait disparaître les termes indexés par
![]() $2$
.
$2$
.
Les propriétés d’inversion des facteurs de transfert nous disent que
![]() $S_{L_{1},L_{2},\unicode[STIX]{x1D6FE}}(\bar{Y}_{1},\bar{Y}_{2},Y_{1},Y_{2})=0$
sauf si
$S_{L_{1},L_{2},\unicode[STIX]{x1D6FE}}(\bar{Y}_{1},\bar{Y}_{2},Y_{1},Y_{2})=0$
sauf si
![]() $\bar{n}_{1}=n_{1}$
,
$\bar{n}_{1}=n_{1}$
,
![]() $\unicode[STIX]{x1D702}_{1}=\unicode[STIX]{x1D702}[L_{1},\unicode[STIX]{x1D6FE}]$
,
$\unicode[STIX]{x1D702}_{1}=\unicode[STIX]{x1D702}[L_{1},\unicode[STIX]{x1D6FE}]$
,
![]() $\bar{n}_{2}=n_{2}$
et
$\bar{n}_{2}=n_{2}$
et
![]() $\unicode[STIX]{x1D702}_{2}=\unicode[STIX]{x1D702}[L_{2},\unicode[STIX]{x1D6FE}]$
.
$\unicode[STIX]{x1D702}_{2}=\unicode[STIX]{x1D702}[L_{2},\unicode[STIX]{x1D6FE}]$
.
Supposons que
![]() $(\bar{n}_{1},\bar{n}_{2})\not =(n_{1},n_{2})$
ou que
$(\bar{n}_{1},\bar{n}_{2})\not =(n_{1},n_{2})$
ou que
![]() $(\bar{n}_{1},\bar{n}_{2})=(n_{1},n_{2})$
mais que
$(\bar{n}_{1},\bar{n}_{2})=(n_{1},n_{2})$
mais que
![]() $(\unicode[STIX]{x1D702}_{1},\unicode[STIX]{x1D702}_{2})$
ne vérifie pas la condition (1) de 2.2 (c’est-à-dire
$(\unicode[STIX]{x1D702}_{1},\unicode[STIX]{x1D702}_{2})$
ne vérifie pas la condition (1) de 2.2 (c’est-à-dire
![]() $\operatorname{val}_{F}(\unicode[STIX]{x1D702}_{1})\equiv t_{1}^{\prime }=t_{1}^{\prime \prime }\,\,\text{mod}\,\,2\,\mathbb{Z}$
et
$\operatorname{val}_{F}(\unicode[STIX]{x1D702}_{1})\equiv t_{1}^{\prime }=t_{1}^{\prime \prime }\,\,\text{mod}\,\,2\,\mathbb{Z}$
et
![]() $\operatorname{val}_{F}(\unicode[STIX]{x1D702}_{2})\equiv t_{2}^{\prime }=t_{2}^{\prime \prime }\,\,\text{mod}\,\,2\,\mathbb{Z}$
). Remarquons que les couples
$\operatorname{val}_{F}(\unicode[STIX]{x1D702}_{2})\equiv t_{2}^{\prime }=t_{2}^{\prime \prime }\,\,\text{mod}\,\,2\,\mathbb{Z}$
). Remarquons que les couples
![]() $(\unicode[STIX]{x1D702}[L_{1},\unicode[STIX]{x1D6FE}],\unicode[STIX]{x1D702}[L_{2},\unicode[STIX]{x1D6FE}])$
dépendent de
$(\unicode[STIX]{x1D702}[L_{1},\unicode[STIX]{x1D6FE}],\unicode[STIX]{x1D702}[L_{2},\unicode[STIX]{x1D6FE}])$
dépendent de
![]() $L_{1}$
,
$L_{1}$
,
![]() $L_{2}$
et
$L_{2}$
et
![]() $\unicode[STIX]{x1D6FE}$
mais vérifient par construction cette condition. Alors
$\unicode[STIX]{x1D6FE}$
mais vérifient par construction cette condition. Alors
![]() $S_{L_{1},L_{2},\unicode[STIX]{x1D6FE}}(\bar{Y}_{1},\bar{Y}_{2},Y_{1},Y_{2})$
est toujours nulle. Donc
$S_{L_{1},L_{2},\unicode[STIX]{x1D6FE}}(\bar{Y}_{1},\bar{Y}_{2},Y_{1},Y_{2})$
est toujours nulle. Donc
![]() $E[a,L_{1},L_{2}](\bar{Y}_{1},\bar{Y}_{2})$
aussi. La formule (2) implique que
$E[a,L_{1},L_{2}](\bar{Y}_{1},\bar{Y}_{2})$
aussi. La formule (2) implique que
![]() $J^{\operatorname{endo}}(\bar{Y}_{1},\bar{Y}_{2},f)=0$
. Cela étant vrai pour tous
$J^{\operatorname{endo}}(\bar{Y}_{1},\bar{Y}_{2},f)=0$
. Cela étant vrai pour tous
![]() $\bar{Y}_{1},\bar{Y}_{2}$
, on a
$\bar{Y}_{1},\bar{Y}_{2}$
, on a
![]() $\text{transfert}_{\bar{n}_{1},\unicode[STIX]{x1D702}_{1},\bar{n}_{2},\unicode[STIX]{x1D702}_{2}}(f)=0$
. Cela démontre le (ii) du lemme 2.2.
$\text{transfert}_{\bar{n}_{1},\unicode[STIX]{x1D702}_{1},\bar{n}_{2},\unicode[STIX]{x1D702}_{2}}(f)=0$
. Cela démontre le (ii) du lemme 2.2.
2.8 Démonstration du (i) du lemme 2.2
On poursuit le calcul en supposant que
![]() $\bar{n}_{1}=n_{1}$
,
$\bar{n}_{1}=n_{1}$
,
![]() $\bar{n}_{2}=n_{2}$
et que
$\bar{n}_{2}=n_{2}$
et que
![]() $(\unicode[STIX]{x1D702}_{1},\unicode[STIX]{x1D702}_{2})$
vérifient la condition (1) de 2.2.
$(\unicode[STIX]{x1D702}_{1},\unicode[STIX]{x1D702}_{2})$
vérifient la condition (1) de 2.2.
Le terme
![]() $E[a,L_{1},L_{2}](\bar{Y}_{1},\bar{Y}_{2})$
n’est non nul que si
$E[a,L_{1},L_{2}](\bar{Y}_{1},\bar{Y}_{2})$
n’est non nul que si
![]() $\unicode[STIX]{x1D702}[L_{1},\unicode[STIX]{x1D6FE}]=\unicode[STIX]{x1D702}_{1}$
et
$\unicode[STIX]{x1D702}[L_{1},\unicode[STIX]{x1D6FE}]=\unicode[STIX]{x1D702}_{1}$
et
![]() $\unicode[STIX]{x1D702}[L_{2},\unicode[STIX]{x1D6FE}]=\unicode[STIX]{x1D702}_{2}$
. Le couple
$\unicode[STIX]{x1D702}[L_{2},\unicode[STIX]{x1D6FE}]=\unicode[STIX]{x1D702}_{2}$
. Le couple
![]() $(L_{1},L_{2})$
étant fixé, on note
$(L_{1},L_{2})$
étant fixé, on note
![]() $\unicode[STIX]{x1D6E4}[L_{1},L_{2}]$
l’ensemble des
$\unicode[STIX]{x1D6E4}[L_{1},L_{2}]$
l’ensemble des
![]() $\unicode[STIX]{x1D6FE}\in \unicode[STIX]{x1D6E4}$
pour lesquels cette condition est vérifiée. Supposons qu’elle le soit. Alors
$\unicode[STIX]{x1D6FE}\in \unicode[STIX]{x1D6E4}$
pour lesquels cette condition est vérifiée. Supposons qu’elle le soit. Alors
![]() $S_{L_{1},L_{2},\unicode[STIX]{x1D6FE}}(\bar{Y}_{1},\bar{Y}_{2},Y_{1},Y_{2})$
est non nulle si et seulement si
$S_{L_{1},L_{2},\unicode[STIX]{x1D6FE}}(\bar{Y}_{1},\bar{Y}_{2},Y_{1},Y_{2})$
est non nulle si et seulement si
![]() $(Y_{1},Y_{2})$
est stablement conjugué à un couple déduit de
$(Y_{1},Y_{2})$
est stablement conjugué à un couple déduit de
![]() $(\bar{Y}_{1},\bar{Y}_{2})$
par un automorphisme de la donnée endoscopique définie par
$(\bar{Y}_{1},\bar{Y}_{2})$
par un automorphisme de la donnée endoscopique définie par
![]() $(n_{1},n_{2})$
. Si
$(n_{1},n_{2})$
. Si
![]() $(Y_{1},Y_{2})$
est un tel élément,
$(Y_{1},Y_{2})$
est un tel élément,
![]() $S_{L_{1},L_{2},\unicode[STIX]{x1D6FE}}(\bar{Y}_{1},\bar{Y}_{2},Y_{1},Y_{2})$
est égal au nombre de termes de la sommation, c’est-à-dire au nombre
$S_{L_{1},L_{2},\unicode[STIX]{x1D6FE}}(\bar{Y}_{1},\bar{Y}_{2},Y_{1},Y_{2})$
est égal au nombre de termes de la sommation, c’est-à-dire au nombre
![]() $z(\bar{Y}_{1},\bar{Y}_{2})$
de classes de conjugaison dans la classe totale de conjugaison stable de
$z(\bar{Y}_{1},\bar{Y}_{2})$
de classes de conjugaison dans la classe totale de conjugaison stable de
![]() $\mathfrak{g}_{\operatorname{iso}}(F)\cup \mathfrak{g}_{\operatorname{an}}(F)$
correspondant à celle de
$\mathfrak{g}_{\operatorname{iso}}(F)\cup \mathfrak{g}_{\operatorname{an}}(F)$
correspondant à celle de
![]() $(\bar{Y}_{1},\bar{Y}_{2})$
.
$(\bar{Y}_{1},\bar{Y}_{2})$
.
Il faut faire attention ici. Parce que l’on travaille simultanément avec les deux groupes
![]() $G_{\operatorname{iso}}$
et
$G_{\operatorname{iso}}$
et
![]() $G_{\operatorname{an}}$
, on a raffiné la notion de donnée endoscopique. Il faut raffiner aussi celle d’automorphismes de cette donnée. On voit que, si
$G_{\operatorname{an}}$
, on a raffiné la notion de donnée endoscopique. Il faut raffiner aussi celle d’automorphismes de cette donnée. On voit que, si
![]() $n_{1}$
et
$n_{1}$
et
![]() $n_{2}$
sont tous deux non nuls, il y a deux automorphismes de notre donnée : outre l’identité, il y a l’action d’un élément de
$n_{2}$
sont tous deux non nuls, il y a deux automorphismes de notre donnée : outre l’identité, il y a l’action d’un élément de
![]() $O^{-}(Q_{n_{1},\unicode[STIX]{x1D702}_{1},\operatorname{iso}})\times O^{-}(Q_{n_{2},\unicode[STIX]{x1D702}_{2},\operatorname{iso}})$
.
$O^{-}(Q_{n_{1},\unicode[STIX]{x1D702}_{1},\operatorname{iso}})\times O^{-}(Q_{n_{2},\unicode[STIX]{x1D702}_{2},\operatorname{iso}})$
.
Remarque.
Dans le cas où
![]() $n_{1}=n_{2}$
et
$n_{1}=n_{2}$
et
![]() $\unicode[STIX]{x1D702}_{1}=\unicode[STIX]{x1D702}_{2}$
, la permutation des deux groupes
$\unicode[STIX]{x1D702}_{1}=\unicode[STIX]{x1D702}_{2}$
, la permutation des deux groupes
![]() $G_{n_{1},\unicode[STIX]{x1D702}_{1},\operatorname{iso}}$
et
$G_{n_{1},\unicode[STIX]{x1D702}_{1},\operatorname{iso}}$
et
![]() $G_{n_{2},\unicode[STIX]{x1D702}_{2},\operatorname{iso}}$
n’est pas un automorphisme pour notre notion de donnée endoscopique.
$G_{n_{2},\unicode[STIX]{x1D702}_{2},\operatorname{iso}}$
n’est pas un automorphisme pour notre notion de donnée endoscopique.
Soit
![]() $(Y_{1},Y_{2})$
un couple stablement conjugué à
$(Y_{1},Y_{2})$
un couple stablement conjugué à
![]() $(\bar{Y}_{1},\bar{Y}_{2})$
. Notons
$(\bar{Y}_{1},\bar{Y}_{2})$
. Notons
![]() $(\text{}\underline{Y}_{1},\text{}\underline{Y}_{2})$
le couple déduit de
$(\text{}\underline{Y}_{1},\text{}\underline{Y}_{2})$
le couple déduit de
![]() $(Y_{1},Y_{2})$
par l’automorphisme non trivial. Il n’est pas stablement conjugué à
$(Y_{1},Y_{2})$
par l’automorphisme non trivial. Il n’est pas stablement conjugué à
![]() $(\bar{Y}_{1},\bar{Y}_{2})$
. Cependant, les fonctions
$(\bar{Y}_{1},\bar{Y}_{2})$
. Cependant, les fonctions
![]() $\hat{i} _{\operatorname{iso}}[a^{L_{1}},e_{1},u_{1}]$
et
$\hat{i} _{\operatorname{iso}}[a^{L_{1}},e_{1},u_{1}]$
et
![]() $\hat{i} _{\operatorname{iso}}[a^{L_{2}},e_{2},u_{2}]$
sont invariantes par conjugaison non seulement par les groupes spéciaux orthogonaux, mais aussi par les groupes orthogonaux tout entiers. Cela vient de la définition de ces fonctions : par exemple,
$\hat{i} _{\operatorname{iso}}[a^{L_{2}},e_{2},u_{2}]$
sont invariantes par conjugaison non seulement par les groupes spéciaux orthogonaux, mais aussi par les groupes orthogonaux tout entiers. Cela vient de la définition de ces fonctions : par exemple,
![]() $\hat{i} _{\operatorname{iso}}[a^{L_{1}},e_{1},u_{1}]$
est la somme de deux fonctions associées à
$\hat{i} _{\operatorname{iso}}[a^{L_{1}},e_{1},u_{1}]$
est la somme de deux fonctions associées à
![]() $X^{+}(a^{L_{1}},e_{1},u_{1})$
et
$X^{+}(a^{L_{1}},e_{1},u_{1})$
et
![]() $X^{-}(a^{L_{1}},e_{1},u_{1})$
, et ces deux éléments sont justement conjugués par un élément du groupe orthogonal de déterminant
$X^{-}(a^{L_{1}},e_{1},u_{1})$
, et ces deux éléments sont justement conjugués par un élément du groupe orthogonal de déterminant
![]() $-1$
. On en déduit l’égalité
$-1$
. On en déduit l’égalité
Dans la formule (5) du paragraphe précédent, les couples
![]() $(Y_{1},Y_{2})$
sont simplement ceux qui sont stablement conjugués à
$(Y_{1},Y_{2})$
sont simplement ceux qui sont stablement conjugués à
![]() $(\bar{Y}_{1},\bar{Y}_{2})$
, ainsi que leurs images
$(\bar{Y}_{1},\bar{Y}_{2})$
, ainsi que leurs images
![]() $(\text{}\underline{Y}_{1},\text{}\underline{Y}_{2})$
par automorphisme. Ce qui précède montre que ces derniers donnent la même contribution que les premiers. On peut donc sommer seulement sur les premiers, en multipliant le tout par
$(\text{}\underline{Y}_{1},\text{}\underline{Y}_{2})$
par automorphisme. Ce qui précède montre que ces derniers donnent la même contribution que les premiers. On peut donc sommer seulement sur les premiers, en multipliant le tout par
![]() $2$
. On calcule facilement que
$2$
. On calcule facilement que
![]() $z(\bar{Y}_{1},\bar{Y}_{2})=4z_{\operatorname{iso}}(\bar{Y}_{1})z_{\operatorname{iso}}(\bar{Y}_{2})$
. En posant
$z(\bar{Y}_{1},\bar{Y}_{2})=4z_{\operatorname{iso}}(\bar{Y}_{1})z_{\operatorname{iso}}(\bar{Y}_{2})$
. En posant
![]() $\unicode[STIX]{x1D6FD}=1$
(sous notre hypothèse
$\unicode[STIX]{x1D6FD}=1$
(sous notre hypothèse
![]() $n_{1}\not =0$
,
$n_{1}\not =0$
,
![]() $n_{2}\not =0$
), la formule (5) devient
$n_{2}\not =0$
), la formule (5) devient
 $$\begin{eqnarray}\displaystyle E[a,L_{1},L_{2}](\bar{Y}_{1},\bar{Y}_{2}) & = & \displaystyle 2^{1+2\unicode[STIX]{x1D6FD}}C(n_{1},\unicode[STIX]{x1D702}_{1},n_{2},\unicode[STIX]{x1D702}_{2})\mathop{\sum }_{(Y_{1},Y_{2})}\nonumber\\ \displaystyle & & \displaystyle \times \,\mathop{\sum }_{e_{1}\in {\mathcal{E}}_{1},u_{1}\in {\mathcal{U}}_{1},e_{2}\in {\mathcal{E}}_{2},u_{2}\in {\mathcal{U}}_{2}}\nonumber\\ \displaystyle & & \displaystyle \times \,\hat{i} _{\operatorname{iso}}[a^{L_{1}},e_{1},u_{1}](Y_{1})\hat{i} _{\operatorname{iso}}[a^{L_{2}},e_{2},u_{2}](Y_{2}),\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle E[a,L_{1},L_{2}](\bar{Y}_{1},\bar{Y}_{2}) & = & \displaystyle 2^{1+2\unicode[STIX]{x1D6FD}}C(n_{1},\unicode[STIX]{x1D702}_{1},n_{2},\unicode[STIX]{x1D702}_{2})\mathop{\sum }_{(Y_{1},Y_{2})}\nonumber\\ \displaystyle & & \displaystyle \times \,\mathop{\sum }_{e_{1}\in {\mathcal{E}}_{1},u_{1}\in {\mathcal{U}}_{1},e_{2}\in {\mathcal{E}}_{2},u_{2}\in {\mathcal{U}}_{2}}\nonumber\\ \displaystyle & & \displaystyle \times \,\hat{i} _{\operatorname{iso}}[a^{L_{1}},e_{1},u_{1}](Y_{1})\hat{i} _{\operatorname{iso}}[a^{L_{2}},e_{2},u_{2}](Y_{2}),\nonumber\end{eqnarray}$$
où l’on somme sur les couples
![]() $(Y_{1},Y_{2})$
stablement conjugués à
$(Y_{1},Y_{2})$
stablement conjugués à
![]() $(\bar{Y}_{1},\bar{Y}_{2})$
, pris à conjugaison près.
$(\bar{Y}_{1},\bar{Y}_{2})$
, pris à conjugaison près.
Si par exemple
![]() $n_{2}=0$
, notre donnée endoscopique n’a pas d’autre automorphisme que l’identité. Mais on a cette fois l’égalité
$n_{2}=0$
, notre donnée endoscopique n’a pas d’autre automorphisme que l’identité. Mais on a cette fois l’égalité
![]() $z(\bar{Y}_{1})=2z_{\operatorname{iso}}(\bar{Y}_{1})$
. Le calcul conduit à la même égalité que ci-dessus, où
$z(\bar{Y}_{1})=2z_{\operatorname{iso}}(\bar{Y}_{1})$
. Le calcul conduit à la même égalité que ci-dessus, où
![]() $\unicode[STIX]{x1D6FD}=0$
maintenant.
$\unicode[STIX]{x1D6FD}=0$
maintenant.
La formule (2) de 2.7 devient
 $$\begin{eqnarray}\displaystyle J^{\operatorname{endo}}(\bar{Y}_{1},\bar{Y}_{2},f) & = & \displaystyle 2^{1+2\unicode[STIX]{x1D6FD}}C(n_{1},\unicode[STIX]{x1D702}_{1},n_{2},\unicode[STIX]{x1D702}_{2})|{\mathcal{L}}|^{-1}\mathop{\sum }_{(Y_{1},Y_{2})}\mathop{\sum }_{(L_{1},L_{2})\in {\mathcal{L}}}\mathop{\sum }_{\unicode[STIX]{x1D6FE}\in \unicode[STIX]{x1D6E4}[L_{1},L_{2}]}\nonumber\\ \displaystyle & & \displaystyle \times \,C(\unicode[STIX]{x1D6FE},L_{2})\int _{A(\unicode[STIX]{x1D6FE})}\mathop{\sum }_{e_{1}\in {\mathcal{E}}_{1},u_{1}\in {\mathcal{U}}_{1},e_{2}\in {\mathcal{E}}_{2},u_{2}\in {\mathcal{U}}_{2}}\nonumber\\ \displaystyle & & \displaystyle \times \,\hat{i} _{\operatorname{iso}}[a^{L_{1}},e_{1},u_{1}](Y_{1})\hat{i} _{\operatorname{iso}}[a^{L_{2}},e_{2},u_{2}](Y_{2})\,da,\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle J^{\operatorname{endo}}(\bar{Y}_{1},\bar{Y}_{2},f) & = & \displaystyle 2^{1+2\unicode[STIX]{x1D6FD}}C(n_{1},\unicode[STIX]{x1D702}_{1},n_{2},\unicode[STIX]{x1D702}_{2})|{\mathcal{L}}|^{-1}\mathop{\sum }_{(Y_{1},Y_{2})}\mathop{\sum }_{(L_{1},L_{2})\in {\mathcal{L}}}\mathop{\sum }_{\unicode[STIX]{x1D6FE}\in \unicode[STIX]{x1D6E4}[L_{1},L_{2}]}\nonumber\\ \displaystyle & & \displaystyle \times \,C(\unicode[STIX]{x1D6FE},L_{2})\int _{A(\unicode[STIX]{x1D6FE})}\mathop{\sum }_{e_{1}\in {\mathcal{E}}_{1},u_{1}\in {\mathcal{U}}_{1},e_{2}\in {\mathcal{E}}_{2},u_{2}\in {\mathcal{U}}_{2}}\nonumber\\ \displaystyle & & \displaystyle \times \,\hat{i} _{\operatorname{iso}}[a^{L_{1}},e_{1},u_{1}](Y_{1})\hat{i} _{\operatorname{iso}}[a^{L_{2}},e_{2},u_{2}](Y_{2})\,da,\end{eqnarray}$$
la somme en
![]() $(Y_{1},Y_{2})$
étant comme ci-dessus.
$(Y_{1},Y_{2})$
étant comme ci-dessus.
Rappelons qu’en 2.4, on a fixé des ensembles
![]() $\unicode[STIX]{x1D6E4}_{0}$
et
$\unicode[STIX]{x1D6E4}_{0}$
et
![]() $\unicode[STIX]{x1D6E4}_{j}$
pour
$\unicode[STIX]{x1D6E4}_{j}$
pour
![]() $j=(R-r)/2+1,\ldots ,R$
. Introduisons l’ensemble
$j=(R-r)/2+1,\ldots ,R$
. Introduisons l’ensemble
![]() $\boldsymbol{\unicode[STIX]{x1D6E4}}$
des familles
$\boldsymbol{\unicode[STIX]{x1D6E4}}$
des familles
![]() $\unicode[STIX]{x1D6E4}^{\ast }=((\unicode[STIX]{x1D6E4}_{1,j})_{j=1,\ldots ,t_{1}^{\prime }},(\unicode[STIX]{x1D6E4}_{2,j})_{j=1,\ldots ,t_{2}^{\prime }})$
qui vérifient les conditions suivantes :
$\unicode[STIX]{x1D6E4}^{\ast }=((\unicode[STIX]{x1D6E4}_{1,j})_{j=1,\ldots ,t_{1}^{\prime }},(\unicode[STIX]{x1D6E4}_{2,j})_{j=1,\ldots ,t_{2}^{\prime }})$
qui vérifient les conditions suivantes :
pour
![]() $j=t_{2}^{\prime }+1,\ldots ,t_{1}^{\prime }$
,
$j=t_{2}^{\prime }+1,\ldots ,t_{1}^{\prime }$
,
![]() $\unicode[STIX]{x1D6E4}_{1,j}=\unicode[STIX]{x1D6E4}_{j+(R-r)/2}$
;
$\unicode[STIX]{x1D6E4}_{1,j}=\unicode[STIX]{x1D6E4}_{j+(R-r)/2}$
;
pour
![]() $j=1,\ldots ,t_{2}^{\prime }$
,
$j=1,\ldots ,t_{2}^{\prime }$
,
![]() $\unicode[STIX]{x1D6E4}_{1,j}$
, respectivement
$\unicode[STIX]{x1D6E4}_{1,j}$
, respectivement
![]() $\unicode[STIX]{x1D6E4}_{2,j}$
, est un sous-ensemble de
$\unicode[STIX]{x1D6E4}_{2,j}$
, est un sous-ensemble de
![]() $\unicode[STIX]{x1D6E4}_{0}$
à deux éléments, qui est un ensemble de représentants de
$\unicode[STIX]{x1D6E4}_{0}$
à deux éléments, qui est un ensemble de représentants de
![]() $\mathfrak{o}^{\times }/\mathfrak{o}^{\times 2}$
; on impose
$\mathfrak{o}^{\times }/\mathfrak{o}^{\times 2}$
; on impose
![]() $\unicode[STIX]{x1D6E4}_{1,j}\cap \unicode[STIX]{x1D6E4}_{2,j}=\emptyset$
.
$\unicode[STIX]{x1D6E4}_{1,j}\cap \unicode[STIX]{x1D6E4}_{2,j}=\emptyset$
.
Pour une telle famille, on note
![]() $\unicode[STIX]{x1D6E4}_{\unicode[STIX]{x1D702}_{1}}^{\ast }$
l’ensemble des familles
$\unicode[STIX]{x1D6E4}_{\unicode[STIX]{x1D702}_{1}}^{\ast }$
l’ensemble des familles
![]() $\unicode[STIX]{x1D6FE}_{1}=(\unicode[STIX]{x1D6FE}_{1,j})_{j=1,\ldots ,t_{1}^{\prime }}\in \prod _{j=1,\ldots ,t_{1}^{\prime }}\unicode[STIX]{x1D6E4}_{1,j}$
qui vérifient la condition
$\unicode[STIX]{x1D6FE}_{1}=(\unicode[STIX]{x1D6FE}_{1,j})_{j=1,\ldots ,t_{1}^{\prime }}\in \prod _{j=1,\ldots ,t_{1}^{\prime }}\unicode[STIX]{x1D6E4}_{1,j}$
qui vérifient la condition
![]() $\operatorname{sgn}(\unicode[STIX]{x1D702}_{1}\unicode[STIX]{x1D71B}^{-\operatorname{val}_{F}(\unicode[STIX]{x1D702}_{1})}\prod _{j=1,\ldots ,t_{1}^{\prime }}\unicode[STIX]{x1D6FE}_{1,j})=\operatorname{sgn}_{CD}(w^{\prime })$
.
$\operatorname{sgn}(\unicode[STIX]{x1D702}_{1}\unicode[STIX]{x1D71B}^{-\operatorname{val}_{F}(\unicode[STIX]{x1D702}_{1})}\prod _{j=1,\ldots ,t_{1}^{\prime }}\unicode[STIX]{x1D6FE}_{1,j})=\operatorname{sgn}_{CD}(w^{\prime })$
.
On définit l’ensemble
![]() $\unicode[STIX]{x1D6E4}_{\unicode[STIX]{x1D702}_{2}}^{\ast }$
en changeant les indices
$\unicode[STIX]{x1D6E4}_{\unicode[STIX]{x1D702}_{2}}^{\ast }$
en changeant les indices
![]() $1$
en
$1$
en
![]() $2$
et
$2$
et
![]() $w^{\prime }$
en
$w^{\prime }$
en
![]() $w^{\prime \prime }$
.
$w^{\prime \prime }$
.
Fixons
![]() $(L_{1},L_{2})\in {\mathcal{L}}$
. Pour
$(L_{1},L_{2})\in {\mathcal{L}}$
. Pour
![]() $(\unicode[STIX]{x1D6FE}_{1},\unicode[STIX]{x1D6FE}_{2})\in \unicode[STIX]{x1D6E4}_{\unicode[STIX]{x1D702}_{1}}^{\ast }\times \unicode[STIX]{x1D6E4}_{\unicode[STIX]{x1D702}_{2}}^{\ast }$
, on définit une famille
$(\unicode[STIX]{x1D6FE}_{1},\unicode[STIX]{x1D6FE}_{2})\in \unicode[STIX]{x1D6E4}_{\unicode[STIX]{x1D702}_{1}}^{\ast }\times \unicode[STIX]{x1D6E4}_{\unicode[STIX]{x1D702}_{2}}^{\ast }$
, on définit une famille
![]() $\unicode[STIX]{x1D6FE}=(\unicode[STIX]{x1D6FE}_{l})_{l=1,\ldots ,R}$
de la façon suivante
$\unicode[STIX]{x1D6FE}=(\unicode[STIX]{x1D6FE}_{l})_{l=1,\ldots ,R}$
de la façon suivante
pour
![]() $j=t_{2}^{\prime }+1,\ldots ,t_{1}^{\prime }$
,
$j=t_{2}^{\prime }+1,\ldots ,t_{1}^{\prime }$
,
![]() $\unicode[STIX]{x1D6FE}_{j+(R-r)/2}=\unicode[STIX]{x1D6FE}_{1,j}$
;
$\unicode[STIX]{x1D6FE}_{j+(R-r)/2}=\unicode[STIX]{x1D6FE}_{1,j}$
;
pour
![]() $j=1,\ldots ,t_{2}^{\prime }$
,
$j=1,\ldots ,t_{2}^{\prime }$
,
![]() $\unicode[STIX]{x1D6FE}_{l_{1}(j)}=\unicode[STIX]{x1D6FE}_{1,j}$
et
$\unicode[STIX]{x1D6FE}_{l_{1}(j)}=\unicode[STIX]{x1D6FE}_{1,j}$
et
![]() $\unicode[STIX]{x1D6FE}_{l_{2}(j)}=\unicode[STIX]{x1D6FE}_{2,j}$
.
$\unicode[STIX]{x1D6FE}_{l_{2}(j)}=\unicode[STIX]{x1D6FE}_{2,j}$
.
On vérifie que cette famille appartient à
![]() $\unicode[STIX]{x1D6E4}$
. Cela définit une application
$\unicode[STIX]{x1D6E4}$
. Cela définit une application
Montrons que
(2) l’image de
![]() $\unicode[STIX]{x1D70B}_{L_{1},L_{2}}$
est égale à
$\unicode[STIX]{x1D70B}_{L_{1},L_{2}}$
est égale à
![]() $\unicode[STIX]{x1D6E4}[L_{1},L_{2}]$
; pour
$\unicode[STIX]{x1D6E4}[L_{1},L_{2}]$
; pour
![]() $\unicode[STIX]{x1D6FE}=(\unicode[STIX]{x1D6FE}_{l})_{l=1,\ldots ,R}\in \unicode[STIX]{x1D6E4}[L_{1},L_{2}]$
, la fibre de
$\unicode[STIX]{x1D6FE}=(\unicode[STIX]{x1D6FE}_{l})_{l=1,\ldots ,R}\in \unicode[STIX]{x1D6E4}[L_{1},L_{2}]$
, la fibre de
![]() $\unicode[STIX]{x1D70B}_{L_{1},L_{2}}$
au-dessus de
$\unicode[STIX]{x1D70B}_{L_{1},L_{2}}$
au-dessus de
![]() $\unicode[STIX]{x1D6FE}$
a pour nombre d’éléments
$\unicode[STIX]{x1D6FE}$
a pour nombre d’éléments
Soit
![]() $\unicode[STIX]{x1D6E4}^{\ast }\in \boldsymbol{\unicode[STIX]{x1D6E4}}$
et
$\unicode[STIX]{x1D6E4}^{\ast }\in \boldsymbol{\unicode[STIX]{x1D6E4}}$
et
![]() $(\unicode[STIX]{x1D6FE}_{1},\unicode[STIX]{x1D6FE}_{2})\in \unicode[STIX]{x1D6E4}_{\unicode[STIX]{x1D702}_{1}}^{\ast }\times \unicode[STIX]{x1D6E4}_{\unicode[STIX]{x1D702}_{2}}^{\ast }$
. Posons
$(\unicode[STIX]{x1D6FE}_{1},\unicode[STIX]{x1D6FE}_{2})\in \unicode[STIX]{x1D6E4}_{\unicode[STIX]{x1D702}_{1}}^{\ast }\times \unicode[STIX]{x1D6E4}_{\unicode[STIX]{x1D702}_{2}}^{\ast }$
. Posons
![]() $\unicode[STIX]{x1D6FE}=\unicode[STIX]{x1D70B}_{L_{1},L_{2}}(\unicode[STIX]{x1D6FE}_{1},\unicode[STIX]{x1D6FE}_{2})$
. On a défini en 2.6 des éléments
$\unicode[STIX]{x1D6FE}=\unicode[STIX]{x1D70B}_{L_{1},L_{2}}(\unicode[STIX]{x1D6FE}_{1},\unicode[STIX]{x1D6FE}_{2})$
. On a défini en 2.6 des éléments
![]() $\unicode[STIX]{x1D6FE}^{L_{1}}$
et
$\unicode[STIX]{x1D6FE}^{L_{1}}$
et
![]() $\unicode[STIX]{x1D6FE}^{L_{2}}$
. Ils ne sont autres que
$\unicode[STIX]{x1D6FE}^{L_{2}}$
. Ils ne sont autres que
![]() $\unicode[STIX]{x1D6FE}_{1}$
et
$\unicode[STIX]{x1D6FE}_{1}$
et
![]() $\unicode[STIX]{x1D6FE}_{2}$
. Le terme
$\unicode[STIX]{x1D6FE}_{2}$
. Le terme
![]() $\unicode[STIX]{x1D702}[L_{2},\unicode[STIX]{x1D6FE}]$
défini en 2.6 est caractérisé par les relations
$\unicode[STIX]{x1D702}[L_{2},\unicode[STIX]{x1D6FE}]$
défini en 2.6 est caractérisé par les relations
![]() $\operatorname{val}_{F}(\unicode[STIX]{x1D702}[L_{2},\unicode[STIX]{x1D6FE}])\equiv t_{2}^{\prime }\,\,\text{mod}\,\,2\,\mathbb{Z}$
et
$\operatorname{val}_{F}(\unicode[STIX]{x1D702}[L_{2},\unicode[STIX]{x1D6FE}])\equiv t_{2}^{\prime }\,\,\text{mod}\,\,2\,\mathbb{Z}$
et
![]() $\operatorname{sgn}(\unicode[STIX]{x1D702}[L_{2},\unicode[STIX]{x1D6FE}]\unicode[STIX]{x1D71B}^{-\operatorname{val}_{F}(\unicode[STIX]{x1D702}[L_{2},\unicode[STIX]{x1D6FE}])}\prod _{j=1,\ldots ,t_{2}^{\prime }}\unicode[STIX]{x1D6FE}_{2,j})=\operatorname{sgn}_{CD}(w^{\prime \prime })$
. Par hypothèse,
$\operatorname{sgn}(\unicode[STIX]{x1D702}[L_{2},\unicode[STIX]{x1D6FE}]\unicode[STIX]{x1D71B}^{-\operatorname{val}_{F}(\unicode[STIX]{x1D702}[L_{2},\unicode[STIX]{x1D6FE}])}\prod _{j=1,\ldots ,t_{2}^{\prime }}\unicode[STIX]{x1D6FE}_{2,j})=\operatorname{sgn}_{CD}(w^{\prime \prime })$
. Par hypothèse,
![]() $\unicode[STIX]{x1D702}_{2}$
vérifie la première relation. Par définition de
$\unicode[STIX]{x1D702}_{2}$
vérifie la première relation. Par définition de
![]() $\unicode[STIX]{x1D6E4}_{\unicode[STIX]{x1D702}_{2}}^{\ast }$
,
$\unicode[STIX]{x1D6E4}_{\unicode[STIX]{x1D702}_{2}}^{\ast }$
,
![]() $\unicode[STIX]{x1D702}_{2}$
vérifie aussi la seconde. Donc
$\unicode[STIX]{x1D702}_{2}$
vérifie aussi la seconde. Donc
![]() $\unicode[STIX]{x1D702}[L_{2},\unicode[STIX]{x1D6FE}]=\unicode[STIX]{x1D702}_{2}$
, puis
$\unicode[STIX]{x1D702}[L_{2},\unicode[STIX]{x1D6FE}]=\unicode[STIX]{x1D702}_{2}$
, puis
![]() $\unicode[STIX]{x1D702}[L_{1},\unicode[STIX]{x1D6FE}]=\unicode[STIX]{x1D702}_{1}$
puisque
$\unicode[STIX]{x1D702}[L_{1},\unicode[STIX]{x1D6FE}]=\unicode[STIX]{x1D702}_{1}$
puisque
![]() $\unicode[STIX]{x1D702}[L_{1},\unicode[STIX]{x1D6FE}]\unicode[STIX]{x1D702}[L_{2},\unicode[STIX]{x1D6FE}]=\unicode[STIX]{x1D702}=\unicode[STIX]{x1D702}_{1}\unicode[STIX]{x1D702}_{2}$
. Par définition de
$\unicode[STIX]{x1D702}[L_{1},\unicode[STIX]{x1D6FE}]\unicode[STIX]{x1D702}[L_{2},\unicode[STIX]{x1D6FE}]=\unicode[STIX]{x1D702}=\unicode[STIX]{x1D702}_{1}\unicode[STIX]{x1D702}_{2}$
. Par définition de
![]() $\unicode[STIX]{x1D6E4}[L_{1},L_{2}]$
,
$\unicode[STIX]{x1D6E4}[L_{1},L_{2}]$
,
![]() $\unicode[STIX]{x1D6FE}$
appartient donc à cet ensemble, ce qui prouve la première assertion. Soit maintenant
$\unicode[STIX]{x1D6FE}$
appartient donc à cet ensemble, ce qui prouve la première assertion. Soit maintenant
![]() $\unicode[STIX]{x1D6FE}\in \unicode[STIX]{x1D6E4}[L_{1},L_{2}]$
. La première partie de la preuve montre que le nombre d’éléments de la fibre de
$\unicode[STIX]{x1D6FE}\in \unicode[STIX]{x1D6E4}[L_{1},L_{2}]$
. La première partie de la preuve montre que le nombre d’éléments de la fibre de
![]() $\unicode[STIX]{x1D70B}_{L_{1},L_{2}}$
au-dessus de
$\unicode[STIX]{x1D70B}_{L_{1},L_{2}}$
au-dessus de
![]() $\unicode[STIX]{x1D6FE}$
est égal au nombre d’éléments
$\unicode[STIX]{x1D6FE}$
est égal au nombre d’éléments
![]() $\unicode[STIX]{x1D6E4}^{\ast }\in \boldsymbol{\unicode[STIX]{x1D6E4}}$
tels que
$\unicode[STIX]{x1D6E4}^{\ast }\in \boldsymbol{\unicode[STIX]{x1D6E4}}$
tels que
![]() $(\unicode[STIX]{x1D6FE}^{L_{1}},\unicode[STIX]{x1D6FE}^{L_{2}})$
appartiennent à
$(\unicode[STIX]{x1D6FE}^{L_{1}},\unicode[STIX]{x1D6FE}^{L_{2}})$
appartiennent à
![]() $(\prod _{j=1,\ldots ,t_{1}^{\prime }}\unicode[STIX]{x1D6E4}_{1,j})\times (\prod _{j=1,\ldots ,t_{2}^{\prime }}\unicode[STIX]{x1D6E4}_{2,j})$
. Ce nombre est le produit sur
$(\prod _{j=1,\ldots ,t_{1}^{\prime }}\unicode[STIX]{x1D6E4}_{1,j})\times (\prod _{j=1,\ldots ,t_{2}^{\prime }}\unicode[STIX]{x1D6E4}_{2,j})$
. Ce nombre est le produit sur
![]() $j=1,\ldots ,t_{2}^{\prime }$
du nombre des paires
$j=1,\ldots ,t_{2}^{\prime }$
du nombre des paires
![]() $(\unicode[STIX]{x1D6E4}_{1,j},\unicode[STIX]{x1D6E4}_{2,j})$
possibles dont le produit contient
$(\unicode[STIX]{x1D6E4}_{1,j},\unicode[STIX]{x1D6E4}_{2,j})$
possibles dont le produit contient
![]() $(\unicode[STIX]{x1D6FE}_{1,j},\unicode[STIX]{x1D6FE}_{2,j})$
. Pour simplifier la notation, posons
$(\unicode[STIX]{x1D6FE}_{1,j},\unicode[STIX]{x1D6FE}_{2,j})$
. Pour simplifier la notation, posons
![]() $x=\unicode[STIX]{x1D6FE}_{1,j}$
,
$x=\unicode[STIX]{x1D6FE}_{1,j}$
,
![]() $y=\unicode[STIX]{x1D6FE}_{2,j}$
. Les éléments
$y=\unicode[STIX]{x1D6FE}_{2,j}$
. Les éléments
![]() $x$
et
$x$
et
![]() $y$
appartiennent à
$y$
appartiennent à
![]() $\unicode[STIX]{x1D6E4}_{0}$
et sont distincts puisqu’ils proviennent de
$\unicode[STIX]{x1D6E4}_{0}$
et sont distincts puisqu’ils proviennent de
![]() $\unicode[STIX]{x1D6FE}\in \unicode[STIX]{x1D6E4}$
. Les paires
$\unicode[STIX]{x1D6FE}\in \unicode[STIX]{x1D6E4}$
. Les paires
![]() $(\unicode[STIX]{x1D6E4}_{1,j},\unicode[STIX]{x1D6E4}_{2,j})$
possibles sont de la forme
$(\unicode[STIX]{x1D6E4}_{1,j},\unicode[STIX]{x1D6E4}_{2,j})$
possibles sont de la forme
![]() $\unicode[STIX]{x1D6E4}_{1,j}=\{x,x^{\prime }\}$
,
$\unicode[STIX]{x1D6E4}_{1,j}=\{x,x^{\prime }\}$
,
![]() $\unicode[STIX]{x1D6E4}_{2,j}=\{y,y^{\prime }\}$
, où
$\unicode[STIX]{x1D6E4}_{2,j}=\{y,y^{\prime }\}$
, où
![]() $x^{\prime }$
et
$x^{\prime }$
et
![]() $y^{\prime }$
sont deux éléments de
$y^{\prime }$
sont deux éléments de
![]() $\unicode[STIX]{x1D6E4}_{0}$
qui vérifient les conditions suivantes :
$\unicode[STIX]{x1D6E4}_{0}$
qui vérifient les conditions suivantes :
![]() $x^{\prime }\not \in x\mathfrak{o}^{\times 2}$
,
$x^{\prime }\not \in x\mathfrak{o}^{\times 2}$
,
![]() $y^{\prime }\not \in y\mathfrak{o}^{\times 2}$
,
$y^{\prime }\not \in y\mathfrak{o}^{\times 2}$
,
![]() $x^{\prime }\not =y$
,
$x^{\prime }\not =y$
,
![]() $y^{\prime }\not =x$
et
$y^{\prime }\not =x$
et
![]() $x^{\prime }\not =y^{\prime }$
.
$x^{\prime }\not =y^{\prime }$
.
Notons
![]() $C_{x}^{\prime }$
l’ensemble des
$C_{x}^{\prime }$
l’ensemble des
![]() $x^{\prime }\in \unicode[STIX]{x1D6E4}_{0}$
tels que
$x^{\prime }\in \unicode[STIX]{x1D6E4}_{0}$
tels que
![]() $x^{\prime }\not \in x\mathfrak{o}^{\times 2}$
et définissons de même
$x^{\prime }\not \in x\mathfrak{o}^{\times 2}$
et définissons de même
![]() $C_{y}^{\prime }$
. Supposons
$C_{y}^{\prime }$
. Supposons
![]() $y\in x\mathfrak{o}^{\times 2}$
, autrement dit
$y\in x\mathfrak{o}^{\times 2}$
, autrement dit
![]() $\operatorname{sgn}(xy)=1$
. On a
$\operatorname{sgn}(xy)=1$
. On a
![]() $C_{x}^{\prime }=C_{y}^{\prime }$
. Les deux premières relations signifient que
$C_{x}^{\prime }=C_{y}^{\prime }$
. Les deux premières relations signifient que
![]() $x^{\prime },y^{\prime }\in C_{x}^{\prime }$
. Cela entraîne les deux relations suivantes :
$x^{\prime },y^{\prime }\in C_{x}^{\prime }$
. Cela entraîne les deux relations suivantes :
![]() $x^{\prime }\not =y$
et
$x^{\prime }\not =y$
et
![]() $y^{\prime }\not =x$
. La dernière relation signifie que
$y^{\prime }\not =x$
. La dernière relation signifie que
![]() $(x^{\prime },y^{\prime })$
n’appartient pas à la diagonale de
$(x^{\prime },y^{\prime })$
n’appartient pas à la diagonale de
![]() $C_{x}^{\prime }\times C_{x}^{\prime }$
. Le nombre de
$C_{x}^{\prime }\times C_{x}^{\prime }$
. Le nombre de
![]() $(x^{\prime },y^{\prime })$
possibles est donc
$(x^{\prime },y^{\prime })$
possibles est donc
![]() $|C_{x}^{\prime }|^{2}-|C_{x}^{\prime }|$
. On a
$|C_{x}^{\prime }|^{2}-|C_{x}^{\prime }|$
. On a
![]() $|C_{x}^{\prime }|=(q-1)/2$
. Le nombre de couples possibles est donc
$|C_{x}^{\prime }|=(q-1)/2$
. Le nombre de couples possibles est donc
![]() $(q-1)(q-3)/4$
, ou encore
$(q-1)(q-3)/4$
, ou encore
![]() $(q-2+\operatorname{sgn}(xy))(q-3)/4$
. Supposons maintenant que
$(q-2+\operatorname{sgn}(xy))(q-3)/4$
. Supposons maintenant que
![]() $y\not \in x\mathfrak{o}^{\times 2}$
, autrement dit que
$y\not \in x\mathfrak{o}^{\times 2}$
, autrement dit que
![]() $\operatorname{sgn}(xy)=-1$
. On a
$\operatorname{sgn}(xy)=-1$
. On a
![]() $C_{x}^{\prime }\not =C_{y}^{\prime }$
. Les première et troisième conditions signifient que
$C_{x}^{\prime }\not =C_{y}^{\prime }$
. Les première et troisième conditions signifient que
![]() $x^{\prime }\in C_{x}^{\prime }-\{y\}$
. De même, les deuxième et quatrième conditions signifient que
$x^{\prime }\in C_{x}^{\prime }-\{y\}$
. De même, les deuxième et quatrième conditions signifient que
![]() $y^{\prime }\in C_{y}^{\prime }-\{x\}$
. La cinquième condition est automatique. Le nombre de
$y^{\prime }\in C_{y}^{\prime }-\{x\}$
. La cinquième condition est automatique. Le nombre de
![]() $(x^{\prime },y^{\prime })$
possibles est donc
$(x^{\prime },y^{\prime })$
possibles est donc
![]() $(|C_{x}^{\prime }|-1)(|C_{y}^{\prime }|-1)=((q-3)/2)^{2}$
, ou encore
$(|C_{x}^{\prime }|-1)(|C_{y}^{\prime }|-1)=((q-3)/2)^{2}$
, ou encore
![]() $(q-2+\operatorname{sgn}(xy))(q-3)/4$
. L’assertion (2) en résulte.
$(q-2+\operatorname{sgn}(xy))(q-3)/4$
. L’assertion (2) en résulte.
Un calcul similaire démontre la relation suivante
(3) le nombre d’éléments de
![]() $\boldsymbol{\unicode[STIX]{x1D6E4}}$
est égal à
$\boldsymbol{\unicode[STIX]{x1D6E4}}$
est égal à
![]() $2^{-4t_{2}^{\prime }}(q-1)^{2t_{2}^{\prime }}(q-3)^{2t_{2}^{\prime }}$
.
$2^{-4t_{2}^{\prime }}(q-1)^{2t_{2}^{\prime }}(q-3)^{2t_{2}^{\prime }}$
.
Pour
![]() $\unicode[STIX]{x1D6E4}^{\ast }\in \boldsymbol{\unicode[STIX]{x1D6E4}}$
,
$\unicode[STIX]{x1D6E4}^{\ast }\in \boldsymbol{\unicode[STIX]{x1D6E4}}$
,
![]() $(L_{1},L_{2})\in {\mathcal{L}}$
et
$(L_{1},L_{2})\in {\mathcal{L}}$
et
![]() $(Y_{1},Y_{2})$
stablement conjugué à
$(Y_{1},Y_{2})$
stablement conjugué à
![]() $(\bar{Y}_{1},\bar{Y}_{2})$
, posons
$(\bar{Y}_{1},\bar{Y}_{2})$
, posons
 $$\begin{eqnarray}\displaystyle {\mathcal{J}}_{\unicode[STIX]{x1D6E4}^{\ast },L_{1},L_{2}}(Y_{1},Y_{2}) & = & \displaystyle 2^{1+2\unicode[STIX]{x1D6FD}}C(n_{1},\unicode[STIX]{x1D702}_{1},n_{2},\unicode[STIX]{x1D702}_{2})\mathop{\sum }_{\unicode[STIX]{x1D6FE}_{1}\in \unicode[STIX]{x1D6E4}_{\unicode[STIX]{x1D702}_{1}}^{\ast }}\mathop{\sum }_{\unicode[STIX]{x1D6FE}_{2}\in \unicode[STIX]{x1D6E4}_{\unicode[STIX]{x1D702}_{2}}^{\ast }}\unicode[STIX]{x1D70E}^{\ast }(\unicode[STIX]{x1D6FE})^{-1}C(\unicode[STIX]{x1D6FE},L_{2})\nonumber\\ \displaystyle & & \displaystyle \times \,\int _{A(\unicode[STIX]{x1D6FE})}\mathop{\sum }_{e_{1}\in {\mathcal{E}}_{1},u_{1}\in {\mathcal{U}}_{1},e_{2}\in {\mathcal{E}}_{2},u_{2}\in {\mathcal{U}}_{2}}\nonumber\\ \displaystyle & & \displaystyle \times \,\hat{i} _{\operatorname{iso}}[a^{L_{1}},e_{1},u_{1}](Y_{1})\hat{i} _{\operatorname{iso}}[a^{L_{2}},e_{2},u_{2}](Y_{2})\,da\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle {\mathcal{J}}_{\unicode[STIX]{x1D6E4}^{\ast },L_{1},L_{2}}(Y_{1},Y_{2}) & = & \displaystyle 2^{1+2\unicode[STIX]{x1D6FD}}C(n_{1},\unicode[STIX]{x1D702}_{1},n_{2},\unicode[STIX]{x1D702}_{2})\mathop{\sum }_{\unicode[STIX]{x1D6FE}_{1}\in \unicode[STIX]{x1D6E4}_{\unicode[STIX]{x1D702}_{1}}^{\ast }}\mathop{\sum }_{\unicode[STIX]{x1D6FE}_{2}\in \unicode[STIX]{x1D6E4}_{\unicode[STIX]{x1D702}_{2}}^{\ast }}\unicode[STIX]{x1D70E}^{\ast }(\unicode[STIX]{x1D6FE})^{-1}C(\unicode[STIX]{x1D6FE},L_{2})\nonumber\\ \displaystyle & & \displaystyle \times \,\int _{A(\unicode[STIX]{x1D6FE})}\mathop{\sum }_{e_{1}\in {\mathcal{E}}_{1},u_{1}\in {\mathcal{U}}_{1},e_{2}\in {\mathcal{E}}_{2},u_{2}\in {\mathcal{U}}_{2}}\nonumber\\ \displaystyle & & \displaystyle \times \,\hat{i} _{\operatorname{iso}}[a^{L_{1}},e_{1},u_{1}](Y_{1})\hat{i} _{\operatorname{iso}}[a^{L_{2}},e_{2},u_{2}](Y_{2})\,da\end{eqnarray}$$
où, pour simplifier, on a posé
![]() $\unicode[STIX]{x1D6FE}=\unicode[STIX]{x1D70B}_{L_{1},L_{2}}(\unicode[STIX]{x1D6FE}_{1},\unicode[STIX]{x1D6FE}_{2})$
. En utilisant (2), on obtient l’égalité
$\unicode[STIX]{x1D6FE}=\unicode[STIX]{x1D70B}_{L_{1},L_{2}}(\unicode[STIX]{x1D6FE}_{1},\unicode[STIX]{x1D6FE}_{2})$
. En utilisant (2), on obtient l’égalité
Fixons
![]() $\unicode[STIX]{x1D6E4}^{\ast }\in \boldsymbol{\unicode[STIX]{x1D6E4}}$
,
$\unicode[STIX]{x1D6E4}^{\ast }\in \boldsymbol{\unicode[STIX]{x1D6E4}}$
,
![]() $(L_{1},L_{2})\in {\mathcal{L}}$
et
$(L_{1},L_{2})\in {\mathcal{L}}$
et
![]() $(Y_{1},Y_{2})$
stablement conjugué à
$(Y_{1},Y_{2})$
stablement conjugué à
![]() $(\bar{Y}_{1},\bar{Y}_{2})$
. Les fonctions
$(\bar{Y}_{1},\bar{Y}_{2})$
. Les fonctions
![]() $f_{1,\unicode[STIX]{x1D702}_{1}}$
et
$f_{1,\unicode[STIX]{x1D702}_{1}}$
et
![]() $f_{2,\unicode[STIX]{x1D702}_{2}}$
qui interviennent dans le lemme 2.2 sont des cas particuliers de notre fonction
$f_{2,\unicode[STIX]{x1D702}_{2}}$
qui interviennent dans le lemme 2.2 sont des cas particuliers de notre fonction
![]() $f$
. Considérons par exemple le cas de l’indice
$f$
. Considérons par exemple le cas de l’indice
![]() $1$
. On passe de
$1$
. On passe de
![]() $f$
à
$f$
à
![]() $f_{1,\unicode[STIX]{x1D702}_{1}}$
en remplaçant
$f_{1,\unicode[STIX]{x1D702}_{1}}$
en remplaçant
![]() $n$
,
$n$
,
![]() $\unicode[STIX]{x1D702}$
,
$\unicode[STIX]{x1D702}$
,
![]() $r^{\prime }$
,
$r^{\prime }$
,
![]() $r^{\prime \prime }$
,
$r^{\prime \prime }$
,
![]() $N^{\prime }$
,
$N^{\prime }$
,
![]() $N^{\prime \prime }$
et
$N^{\prime \prime }$
et
![]() $w^{\prime }$
par
$w^{\prime }$
par
![]() $n_{1}$
,
$n_{1}$
,
![]() $\unicode[STIX]{x1D702}_{1}$
,
$\unicode[STIX]{x1D702}_{1}$
,
![]() $t_{1}^{\prime }$
,
$t_{1}^{\prime }$
,
![]() $t_{1}^{\prime \prime }$
,
$t_{1}^{\prime \prime }$
,
![]() $N^{\prime }$
,
$N^{\prime }$
,
![]() $0$
et
$0$
et
![]() $w^{\prime }$
. Le terme correspondant à
$w^{\prime }$
. Le terme correspondant à
![]() $w^{\prime \prime }$
disparaît. L’intégrale orbitale
$w^{\prime \prime }$
disparaît. L’intégrale orbitale
![]() $J(Y_{1},f_{1,\unicode[STIX]{x1D702}_{1},\operatorname{iso}})$
est calculée par une formule analogue à celle du lemme 2.4. On peut choisir l’ensemble
$J(Y_{1},f_{1,\unicode[STIX]{x1D702}_{1},\operatorname{iso}})$
est calculée par une formule analogue à celle du lemme 2.4. On peut choisir l’ensemble
![]() $\unicode[STIX]{x1D6E4}_{\unicode[STIX]{x1D702}_{1}}^{\ast }$
comme analogue de
$\unicode[STIX]{x1D6E4}_{\unicode[STIX]{x1D702}_{1}}^{\ast }$
comme analogue de
![]() $\unicode[STIX]{x1D6E4}$
. Puisque
$\unicode[STIX]{x1D6E4}$
. Puisque
![]() $t_{1}^{\prime }=t_{1}^{\prime \prime }$
, l’analogue de
$t_{1}^{\prime }=t_{1}^{\prime \prime }$
, l’analogue de
![]() ${\hat{J}}$
est vide. Les analogues de
${\hat{J}}$
est vide. Les analogues de
![]() ${\mathcal{E}}^{0}$
et
${\mathcal{E}}^{0}$
et
![]() ${\mathcal{U}}$
ne sont autres que les ensembles
${\mathcal{U}}$
ne sont autres que les ensembles
![]() ${\mathcal{E}}_{1}$
et
${\mathcal{E}}_{1}$
et
![]() ${\mathcal{U}}_{1}$
déjà introduits. L’analogue de
${\mathcal{U}}_{1}$
déjà introduits. L’analogue de
![]() $\unicode[STIX]{x1D705}^{0}$
est trivial. Parce que
$\unicode[STIX]{x1D705}^{0}$
est trivial. Parce que
![]() $w^{\prime \prime }$
disparaît, l’analogue de
$w^{\prime \prime }$
disparaît, l’analogue de
![]() $\unicode[STIX]{x1D705}^{{\mathcal{U}}}$
est trivial. L’analogue de la constante
$\unicode[STIX]{x1D705}^{{\mathcal{U}}}$
est trivial. L’analogue de la constante
![]() $C(r^{\prime },r^{\prime \prime })$
vaut
$C(r^{\prime },r^{\prime \prime })$
vaut
![]() $2^{1-2t_{1}^{\prime }}$
. On note
$2^{1-2t_{1}^{\prime }}$
. On note
![]() $\unicode[STIX]{x1D6FC}(t_{1}^{\prime },w^{\prime },\unicode[STIX]{x1D702}_{1})$
l’analogue de la constante
$\unicode[STIX]{x1D6FC}(t_{1}^{\prime },w^{\prime },\unicode[STIX]{x1D702}_{1})$
l’analogue de la constante
![]() $\unicode[STIX]{x1D6FC}(r^{\prime },r^{\prime \prime },w^{\prime },w^{\prime \prime })$
. On a donc
$\unicode[STIX]{x1D6FC}(r^{\prime },r^{\prime \prime },w^{\prime },w^{\prime \prime })$
. On a donc
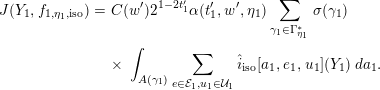 $$\begin{eqnarray}\displaystyle J(Y_{1},f_{1,\unicode[STIX]{x1D702}_{1},\operatorname{iso}}) & = & \displaystyle C(w^{\prime })2^{1-2t_{1}^{\prime }}\unicode[STIX]{x1D6FC}(t_{1}^{\prime },w^{\prime },\unicode[STIX]{x1D702}_{1})\mathop{\sum }_{\unicode[STIX]{x1D6FE}_{1}\in \unicode[STIX]{x1D6E4}_{\unicode[STIX]{x1D702}_{1}}^{\ast }}\unicode[STIX]{x1D70E}(\unicode[STIX]{x1D6FE}_{1})\nonumber\\ \displaystyle & & \displaystyle \times \,\int _{A(\unicode[STIX]{x1D6FE}_{1})}\mathop{\sum }_{e\in {\mathcal{E}}_{1},u_{1}\in {\mathcal{U}}_{1}}\hat{i} _{\operatorname{iso}}[a_{1},e_{1},u_{1}](Y_{1})\,da_{1}.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle J(Y_{1},f_{1,\unicode[STIX]{x1D702}_{1},\operatorname{iso}}) & = & \displaystyle C(w^{\prime })2^{1-2t_{1}^{\prime }}\unicode[STIX]{x1D6FC}(t_{1}^{\prime },w^{\prime },\unicode[STIX]{x1D702}_{1})\mathop{\sum }_{\unicode[STIX]{x1D6FE}_{1}\in \unicode[STIX]{x1D6E4}_{\unicode[STIX]{x1D702}_{1}}^{\ast }}\unicode[STIX]{x1D70E}(\unicode[STIX]{x1D6FE}_{1})\nonumber\\ \displaystyle & & \displaystyle \times \,\int _{A(\unicode[STIX]{x1D6FE}_{1})}\mathop{\sum }_{e\in {\mathcal{E}}_{1},u_{1}\in {\mathcal{U}}_{1}}\hat{i} _{\operatorname{iso}}[a_{1},e_{1},u_{1}](Y_{1})\,da_{1}.\end{eqnarray}$$
Il faut toutefois faire attention : cette formule n’est valable que si
![]() $n_{1}>0$
. En effet, si
$n_{1}>0$
. En effet, si
![]() $n_{1}=0$
, le terme de gauche doit disparaître des calculs qui suivent, autrement dit on doit considérer qu’il vaut
$n_{1}=0$
, le terme de gauche doit disparaître des calculs qui suivent, autrement dit on doit considérer qu’il vaut
![]() $1$
. Les sommes de droite disparaissent, autrement dit valent
$1$
. Les sommes de droite disparaissent, autrement dit valent
![]() $1$
. Les deux constantes
$1$
. Les deux constantes
![]() $C(w^{\prime })$
et
$C(w^{\prime })$
et
![]() $\unicode[STIX]{x1D6FC}(t_{1}^{\prime },w^{\prime },\unicode[STIX]{x1D702}_{1})$
valent aussi
$\unicode[STIX]{x1D6FC}(t_{1}^{\prime },w^{\prime },\unicode[STIX]{x1D702}_{1})$
valent aussi
![]() $1$
. Mais
$1$
. Mais
![]() $2^{1-t_{1}^{\prime }}$
vaut
$2^{1-t_{1}^{\prime }}$
vaut
![]() $2$
et l’égalité n’est pas vérifiée. Bien sûr, c’est le produit des constantes pour les indices
$2$
et l’égalité n’est pas vérifiée. Bien sûr, c’est le produit des constantes pour les indices
![]() $1$
et
$1$
et
![]() $2$
qui va intervenir. La puissance de
$2$
qui va intervenir. La puissance de
![]() $2$
qui intervient dans ce produit est donc
$2$
qui intervient dans ce produit est donc
![]() $2^{2-2t_{1}^{\prime }-2t_{2}^{\prime }}$
si
$2^{2-2t_{1}^{\prime }-2t_{2}^{\prime }}$
si
![]() $n_{1}\not =0$
et
$n_{1}\not =0$
et
![]() $n_{2}\not =0$
et
$n_{2}\not =0$
et
![]() $2^{1-2t_{1}^{\prime }-2t_{2}^{\prime }}$
sinon. Autrement dit, c’est
$2^{1-2t_{1}^{\prime }-2t_{2}^{\prime }}$
sinon. Autrement dit, c’est
![]() $2^{1+\unicode[STIX]{x1D6FD}+2t_{1}^{\prime }+2t_{2}^{\prime }}$
.
$2^{1+\unicode[STIX]{x1D6FD}+2t_{1}^{\prime }+2t_{2}^{\prime }}$
.
Soit
![]() $\unicode[STIX]{x1D6FE}_{1}\in \unicode[STIX]{x1D6E4}_{\unicode[STIX]{x1D702}_{1}}^{\ast }$
,
$\unicode[STIX]{x1D6FE}_{1}\in \unicode[STIX]{x1D6E4}_{\unicode[STIX]{x1D702}_{1}}^{\ast }$
,
![]() $\unicode[STIX]{x1D6FE}_{2}\in \unicode[STIX]{x1D6E4}_{\unicode[STIX]{x1D702}_{2}}^{\ast }$
. Posons
$\unicode[STIX]{x1D6FE}_{2}\in \unicode[STIX]{x1D6E4}_{\unicode[STIX]{x1D702}_{2}}^{\ast }$
. Posons
![]() $\unicode[STIX]{x1D6FE}=\unicode[STIX]{x1D70B}_{L_{1},L_{2}}(\unicode[STIX]{x1D6FE}_{1},\unicode[STIX]{x1D6FE}_{2})$
. Montrons que l’on a l’égalité
$\unicode[STIX]{x1D6FE}=\unicode[STIX]{x1D70B}_{L_{1},L_{2}}(\unicode[STIX]{x1D6FE}_{1},\unicode[STIX]{x1D6FE}_{2})$
. Montrons que l’on a l’égalité
où
 $$\begin{eqnarray}\displaystyle C_{3} & = & \displaystyle \operatorname{sgn}(-1)^{r(R-r)/2}\operatorname{sgn}(\unicode[STIX]{x1D702}\unicode[STIX]{x1D71B}^{-\operatorname{val}_{F}(\unicode[STIX]{x1D702})})^{(R-r)/2}\operatorname{sgn}_{CD}(w^{\prime })^{(R-r)/2}\nonumber\\ \displaystyle & & \displaystyle \times \,\operatorname{sgn}_{CD}(w^{\prime \prime })^{(R-r)/2+\operatorname{val}_{F}(\unicode[STIX]{x1D702})}\nonumber\\ \displaystyle & & \displaystyle \times \,\biggl(\frac{q-3}{4}\biggr)^{-t_{2}^{\prime }}\operatorname{sgn}(-1)^{\operatorname{val}_{F}(\unicode[STIX]{x1D702}_{2})B}\operatorname{sgn}(\unicode[STIX]{x1D702}_{2}\unicode[STIX]{x1D71B}^{-\operatorname{val}_{F}(\unicode[STIX]{x1D702}_{2})})^{B}\operatorname{sgn}_{CD}(w^{\prime \prime })^{B}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle C_{3} & = & \displaystyle \operatorname{sgn}(-1)^{r(R-r)/2}\operatorname{sgn}(\unicode[STIX]{x1D702}\unicode[STIX]{x1D71B}^{-\operatorname{val}_{F}(\unicode[STIX]{x1D702})})^{(R-r)/2}\operatorname{sgn}_{CD}(w^{\prime })^{(R-r)/2}\nonumber\\ \displaystyle & & \displaystyle \times \,\operatorname{sgn}_{CD}(w^{\prime \prime })^{(R-r)/2+\operatorname{val}_{F}(\unicode[STIX]{x1D702})}\nonumber\\ \displaystyle & & \displaystyle \times \,\biggl(\frac{q-3}{4}\biggr)^{-t_{2}^{\prime }}\operatorname{sgn}(-1)^{\operatorname{val}_{F}(\unicode[STIX]{x1D702}_{2})B}\operatorname{sgn}(\unicode[STIX]{x1D702}_{2}\unicode[STIX]{x1D71B}^{-\operatorname{val}_{F}(\unicode[STIX]{x1D702}_{2})})^{B}\operatorname{sgn}_{CD}(w^{\prime \prime })^{B}.\nonumber\end{eqnarray}$$
Rappelons les définitions :
 $$\begin{eqnarray}\displaystyle d(r^{\prime },r^{\prime \prime },\unicode[STIX]{x1D6FE},L_{2}) & = & \displaystyle \operatorname{sgn}(\unicode[STIX]{x1D702}\unicode[STIX]{x1D71B}^{-\operatorname{val}_{F}(\unicode[STIX]{x1D702})})^{(R-r)/2}\operatorname{sgn}_{CD}(w^{\prime })^{(R-r)/2}\nonumber\\ \displaystyle & & \displaystyle \times \,\operatorname{sgn}_{CD}(w^{\prime \prime })^{(R-r)/2+\operatorname{val}_{F}(\unicode[STIX]{x1D702})}\nonumber\\ \displaystyle & & \displaystyle \times \,\left(\displaystyle \mathop{\prod }_{j\in {\hat{J}}}\operatorname{sgn}(\unicode[STIX]{x1D6FE}_{j-1}\unicode[STIX]{x1D6FE}_{j})^{j/2-1}\operatorname{sgn}(\unicode[STIX]{x1D6FE}_{j-1}-\unicode[STIX]{x1D6FE}_{j})\right)\nonumber\\ \displaystyle & & \displaystyle \times \,\left(\displaystyle \mathop{\prod }_{j=R-r+1,\ldots ,R}\operatorname{sgn}(\unicode[STIX]{x1D6FE}_{j})^{(R-r)/2}\right)\nonumber\\ \displaystyle & & \displaystyle \times \,\operatorname{sgn}(-1)^{\operatorname{val}_{F}(\unicode[STIX]{x1D702}_{2})B}\operatorname{sgn}(\unicode[STIX]{x1D702}_{2}\unicode[STIX]{x1D71B}^{-\operatorname{val}_{F}(\unicode[STIX]{x1D702}_{2})})^{B}\operatorname{sgn}_{CD}(w^{\prime \prime })^{B};\nonumber\\ \displaystyle \unicode[STIX]{x1D70E}(\unicode[STIX]{x1D6FE}) & = & \displaystyle \left(\displaystyle \mathop{\prod }_{j\in {\hat{J}}}(q-2+\operatorname{sgn}(\unicode[STIX]{x1D6FE}_{j-1}\unicode[STIX]{x1D6FE}_{j}))\operatorname{sgn}(\unicode[STIX]{x1D6FE}_{j-1}\unicode[STIX]{x1D6FE}_{j}(\unicode[STIX]{x1D6FE}_{j-1}-\unicode[STIX]{x1D6FE}_{j}))\right)\nonumber\\ \displaystyle & & \displaystyle \times \,\displaystyle \mathop{\prod }_{j=R-r+1,\ldots ,R;\,j\,\,\operatorname{impair}}\operatorname{sgn}(-\unicode[STIX]{x1D6FE}_{j});\nonumber\\ \displaystyle \unicode[STIX]{x1D70E}^{\ast }(\unicode[STIX]{x1D6FE}) & = & \displaystyle \biggl(\frac{q-3}{4}\biggr)^{t_{2}^{\prime }}\displaystyle \mathop{\prod }_{l\in {\hat{J}}}(q-2+\operatorname{sgn}(\unicode[STIX]{x1D6FE}_{l-1}\unicode[STIX]{x1D6FE}_{l})).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle d(r^{\prime },r^{\prime \prime },\unicode[STIX]{x1D6FE},L_{2}) & = & \displaystyle \operatorname{sgn}(\unicode[STIX]{x1D702}\unicode[STIX]{x1D71B}^{-\operatorname{val}_{F}(\unicode[STIX]{x1D702})})^{(R-r)/2}\operatorname{sgn}_{CD}(w^{\prime })^{(R-r)/2}\nonumber\\ \displaystyle & & \displaystyle \times \,\operatorname{sgn}_{CD}(w^{\prime \prime })^{(R-r)/2+\operatorname{val}_{F}(\unicode[STIX]{x1D702})}\nonumber\\ \displaystyle & & \displaystyle \times \,\left(\displaystyle \mathop{\prod }_{j\in {\hat{J}}}\operatorname{sgn}(\unicode[STIX]{x1D6FE}_{j-1}\unicode[STIX]{x1D6FE}_{j})^{j/2-1}\operatorname{sgn}(\unicode[STIX]{x1D6FE}_{j-1}-\unicode[STIX]{x1D6FE}_{j})\right)\nonumber\\ \displaystyle & & \displaystyle \times \,\left(\displaystyle \mathop{\prod }_{j=R-r+1,\ldots ,R}\operatorname{sgn}(\unicode[STIX]{x1D6FE}_{j})^{(R-r)/2}\right)\nonumber\\ \displaystyle & & \displaystyle \times \,\operatorname{sgn}(-1)^{\operatorname{val}_{F}(\unicode[STIX]{x1D702}_{2})B}\operatorname{sgn}(\unicode[STIX]{x1D702}_{2}\unicode[STIX]{x1D71B}^{-\operatorname{val}_{F}(\unicode[STIX]{x1D702}_{2})})^{B}\operatorname{sgn}_{CD}(w^{\prime \prime })^{B};\nonumber\\ \displaystyle \unicode[STIX]{x1D70E}(\unicode[STIX]{x1D6FE}) & = & \displaystyle \left(\displaystyle \mathop{\prod }_{j\in {\hat{J}}}(q-2+\operatorname{sgn}(\unicode[STIX]{x1D6FE}_{j-1}\unicode[STIX]{x1D6FE}_{j}))\operatorname{sgn}(\unicode[STIX]{x1D6FE}_{j-1}\unicode[STIX]{x1D6FE}_{j}(\unicode[STIX]{x1D6FE}_{j-1}-\unicode[STIX]{x1D6FE}_{j}))\right)\nonumber\\ \displaystyle & & \displaystyle \times \,\displaystyle \mathop{\prod }_{j=R-r+1,\ldots ,R;\,j\,\,\operatorname{impair}}\operatorname{sgn}(-\unicode[STIX]{x1D6FE}_{j});\nonumber\\ \displaystyle \unicode[STIX]{x1D70E}^{\ast }(\unicode[STIX]{x1D6FE}) & = & \displaystyle \biggl(\frac{q-3}{4}\biggr)^{t_{2}^{\prime }}\displaystyle \mathop{\prod }_{l\in {\hat{J}}}(q-2+\operatorname{sgn}(\unicode[STIX]{x1D6FE}_{l-1}\unicode[STIX]{x1D6FE}_{l})).\nonumber\end{eqnarray}$$
Les formules pour
![]() $\unicode[STIX]{x1D70E}(\unicode[STIX]{x1D6FE}_{1})$
et
$\unicode[STIX]{x1D70E}(\unicode[STIX]{x1D6FE}_{1})$
et
![]() $\unicode[STIX]{x1D70E}(\unicode[STIX]{x1D6FE}_{2})$
se simplifient puisque
$\unicode[STIX]{x1D70E}(\unicode[STIX]{x1D6FE}_{2})$
se simplifient puisque
![]() $t_{1}^{\prime }=t_{1}^{\prime \prime }$
et
$t_{1}^{\prime }=t_{1}^{\prime \prime }$
et
![]() $t_{2}^{\prime }=t_{2}^{\prime \prime }$
:
$t_{2}^{\prime }=t_{2}^{\prime \prime }$
:
 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D70E}(\unicode[STIX]{x1D6FE}_{1}) & = & \displaystyle \displaystyle \mathop{\prod }_{j=1,\ldots ,t_{1}^{\prime };\,j\,\,\operatorname{impair}}\operatorname{sgn}(-\unicode[STIX]{x1D6FE}_{1,j}),\nonumber\\ \displaystyle \unicode[STIX]{x1D70E}(\unicode[STIX]{x1D6FE}_{2}) & = & \displaystyle \displaystyle \mathop{\prod }_{j=1,\ldots ,t_{2}^{\prime };\,j\,\,\operatorname{impair}}\operatorname{sgn}(-\unicode[STIX]{x1D6FE}_{2,j}).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D70E}(\unicode[STIX]{x1D6FE}_{1}) & = & \displaystyle \displaystyle \mathop{\prod }_{j=1,\ldots ,t_{1}^{\prime };\,j\,\,\operatorname{impair}}\operatorname{sgn}(-\unicode[STIX]{x1D6FE}_{1,j}),\nonumber\\ \displaystyle \unicode[STIX]{x1D70E}(\unicode[STIX]{x1D6FE}_{2}) & = & \displaystyle \displaystyle \mathop{\prod }_{j=1,\ldots ,t_{2}^{\prime };\,j\,\,\operatorname{impair}}\operatorname{sgn}(-\unicode[STIX]{x1D6FE}_{2,j}).\nonumber\end{eqnarray}$$
Les restrictions
![]() $j$
impair figurant dans les différents produits peuvent être levées en élevant le terme correspondant (qui est un signe) à la puissance
$j$
impair figurant dans les différents produits peuvent être levées en élevant le terme correspondant (qui est un signe) à la puissance
![]() $j$
. Considérons l’intervention dans le membre de gauche de (6) d’un terme
$j$
. Considérons l’intervention dans le membre de gauche de (6) d’un terme
![]() $\unicode[STIX]{x1D6FE}_{j}$
pour
$\unicode[STIX]{x1D6FE}_{j}$
pour
![]() $j=R-r+1,\ldots ,R$
. Il intervient dans
$j=R-r+1,\ldots ,R$
. Il intervient dans
![]() $d(r^{\prime },r^{\prime \prime },\unicode[STIX]{x1D6FE},L_{2})$
par un facteur
$d(r^{\prime },r^{\prime \prime },\unicode[STIX]{x1D6FE},L_{2})$
par un facteur
![]() $\operatorname{sgn}(\unicode[STIX]{x1D6FE}_{j})^{(R-r)/2}$
et dans
$\operatorname{sgn}(\unicode[STIX]{x1D6FE}_{j})^{(R-r)/2}$
et dans
![]() $\unicode[STIX]{x1D70E}(\unicode[STIX]{x1D6FE})$
par un facteur
$\unicode[STIX]{x1D70E}(\unicode[STIX]{x1D6FE})$
par un facteur
![]() $\operatorname{sgn}(-\unicode[STIX]{x1D6FE}_{j})^{j}$
. Puisque
$\operatorname{sgn}(-\unicode[STIX]{x1D6FE}_{j})^{j}$
. Puisque
![]() $\unicode[STIX]{x1D6FE}_{1,j-(R-r)/2}=\unicode[STIX]{x1D6FE}_{1,j}$
, il intervient dans
$\unicode[STIX]{x1D6FE}_{1,j-(R-r)/2}=\unicode[STIX]{x1D6FE}_{1,j}$
, il intervient dans
![]() $\unicode[STIX]{x1D70E}(\unicode[STIX]{x1D6FE}_{1})$
par un facteur
$\unicode[STIX]{x1D70E}(\unicode[STIX]{x1D6FE}_{1})$
par un facteur
![]() $\operatorname{sgn}(-\unicode[STIX]{x1D6FE}_{j})^{j-(R-r)/2}$
. Le produit de ces contributions est
$\operatorname{sgn}(-\unicode[STIX]{x1D6FE}_{j})^{j-(R-r)/2}$
. Le produit de ces contributions est
![]() $\operatorname{sgn}(-1)^{(R-r)/2}$
. Leur produit sur tous les
$\operatorname{sgn}(-1)^{(R-r)/2}$
. Leur produit sur tous les
![]() $j=R-r+1,\ldots ,R$
est
$j=R-r+1,\ldots ,R$
est
![]() $\operatorname{sgn}(-1)^{r(R-r)/2}$
. Considérons maintenant l’intervention des termes
$\operatorname{sgn}(-1)^{r(R-r)/2}$
. Considérons maintenant l’intervention des termes
![]() $\unicode[STIX]{x1D6FE}_{j-1}$
et
$\unicode[STIX]{x1D6FE}_{j-1}$
et
![]() $\unicode[STIX]{x1D6FE}_{j}$
pour un
$\unicode[STIX]{x1D6FE}_{j}$
pour un
![]() $j\in {\hat{J}}$
. Le terme
$j\in {\hat{J}}$
. Le terme
![]() $\operatorname{sgn}(\unicode[STIX]{x1D6FE}_{j-1}-\unicode[STIX]{x1D6FE}_{j})$
intervient dans
$\operatorname{sgn}(\unicode[STIX]{x1D6FE}_{j-1}-\unicode[STIX]{x1D6FE}_{j})$
intervient dans
![]() $d(r^{\prime },r^{\prime \prime },\unicode[STIX]{x1D6FE},L_{2})$
et dans
$d(r^{\prime },r^{\prime \prime },\unicode[STIX]{x1D6FE},L_{2})$
et dans
![]() $\unicode[STIX]{x1D70E}(\unicode[STIX]{x1D6FE})$
. Il disparaît. Le terme
$\unicode[STIX]{x1D70E}(\unicode[STIX]{x1D6FE})$
. Il disparaît. Le terme
![]() $q-2+\operatorname{sgn}(\unicode[STIX]{x1D6FE}_{j-1}\unicode[STIX]{x1D6FE}_{j})$
intervient dans
$q-2+\operatorname{sgn}(\unicode[STIX]{x1D6FE}_{j-1}\unicode[STIX]{x1D6FE}_{j})$
intervient dans
![]() $\unicode[STIX]{x1D70E}(\unicode[STIX]{x1D6FE})$
et son inverse intervient dans
$\unicode[STIX]{x1D70E}(\unicode[STIX]{x1D6FE})$
et son inverse intervient dans
![]() $\unicode[STIX]{x1D70E}^{\ast }(\unicode[STIX]{x1D6FE})^{-1}$
. Il disparaît. Interviennent
$\unicode[STIX]{x1D70E}^{\ast }(\unicode[STIX]{x1D6FE})^{-1}$
. Il disparaît. Interviennent
![]() $\operatorname{sgn}(\unicode[STIX]{x1D6FE}_{j-1}\unicode[STIX]{x1D6FE}_{j})^{j/2-1}$
dans
$\operatorname{sgn}(\unicode[STIX]{x1D6FE}_{j-1}\unicode[STIX]{x1D6FE}_{j})^{j/2-1}$
dans
![]() $d(r^{\prime },r^{\prime \prime },\unicode[STIX]{x1D6FE},L_{2})$
et
$d(r^{\prime },r^{\prime \prime },\unicode[STIX]{x1D6FE},L_{2})$
et
![]() $\operatorname{sgn}(\unicode[STIX]{x1D6FE}_{j-1}\unicode[STIX]{x1D6FE}_{j})$
dans
$\operatorname{sgn}(\unicode[STIX]{x1D6FE}_{j-1}\unicode[STIX]{x1D6FE}_{j})$
dans
![]() $\unicode[STIX]{x1D70E}(\unicode[STIX]{x1D6FE})$
. Puisque
$\unicode[STIX]{x1D70E}(\unicode[STIX]{x1D6FE})$
. Puisque
![]() $\{\unicode[STIX]{x1D6FE}_{j-1},\unicode[STIX]{x1D6FE}_{j}\}=\{\unicode[STIX]{x1D6FE}_{1,j/2},\unicode[STIX]{x1D6FE}_{2,j/2}\}$
, intervient aussi dans
$\{\unicode[STIX]{x1D6FE}_{j-1},\unicode[STIX]{x1D6FE}_{j}\}=\{\unicode[STIX]{x1D6FE}_{1,j/2},\unicode[STIX]{x1D6FE}_{2,j/2}\}$
, intervient aussi dans
![]() $\unicode[STIX]{x1D70E}(\unicode[STIX]{x1D6FE}_{1})\unicode[STIX]{x1D70E}(\unicode[STIX]{x1D6FE}_{2})$
le terme
$\unicode[STIX]{x1D70E}(\unicode[STIX]{x1D6FE}_{1})\unicode[STIX]{x1D70E}(\unicode[STIX]{x1D6FE}_{2})$
le terme
![]() $\operatorname{sgn}(\unicode[STIX]{x1D6FE}_{j-1}\unicode[STIX]{x1D6FE}_{j})^{j/2}$
. Le produit de ces termes vaut
$\operatorname{sgn}(\unicode[STIX]{x1D6FE}_{j-1}\unicode[STIX]{x1D6FE}_{j})^{j/2}$
. Le produit de ces termes vaut
![]() $1$
. En résumé, la contribution des termes dépendant des
$1$
. En résumé, la contribution des termes dépendant des
![]() $\unicode[STIX]{x1D6FE}_{j}$
est
$\unicode[STIX]{x1D6FE}_{j}$
est
![]() $\operatorname{sgn}(-1)^{r(R-r)/2}$
. Outre ce terme, il reste le produit des constantes. Le tout donne la formule (7).
$\operatorname{sgn}(-1)^{r(R-r)/2}$
. Outre ce terme, il reste le produit des constantes. Le tout donne la formule (7).
Dans la formule (4) interviennent des termes
![]() $\unicode[STIX]{x1D6FE}$
,
$\unicode[STIX]{x1D6FE}$
,
![]() $a$
,
$a$
,
![]() $a^{L_{1}}$
et
$a^{L_{1}}$
et
![]() $a^{L_{2}}$
. On a vu dans la preuve de (2) que
$a^{L_{2}}$
. On a vu dans la preuve de (2) que
![]() $\unicode[STIX]{x1D6FE}^{L_{1}}=\unicode[STIX]{x1D6FE}_{1}$
et
$\unicode[STIX]{x1D6FE}^{L_{1}}=\unicode[STIX]{x1D6FE}_{1}$
et
![]() $\unicode[STIX]{x1D6FE}^{L_{2}}=\unicode[STIX]{x1D6FE}_{2}$
. On voit que, quand
$\unicode[STIX]{x1D6FE}^{L_{2}}=\unicode[STIX]{x1D6FE}_{2}$
. On voit que, quand
![]() $a$
décrit
$a$
décrit
![]() $A(\unicode[STIX]{x1D6FE})$
, le couple
$A(\unicode[STIX]{x1D6FE})$
, le couple
![]() $(a^{L_{1}},a^{L_{2}})$
décrit
$(a^{L_{1}},a^{L_{2}})$
décrit
![]() $A(\unicode[STIX]{x1D6FE}_{1})\times A(\unicode[STIX]{x1D6FE}_{2})$
. La formule (4) se récrit
$A(\unicode[STIX]{x1D6FE}_{1})\times A(\unicode[STIX]{x1D6FE}_{2})$
. La formule (4) se récrit
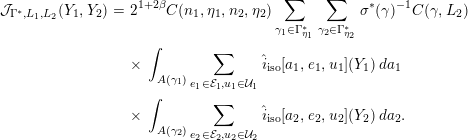 $$\begin{eqnarray}\displaystyle {\mathcal{J}}_{\unicode[STIX]{x1D6E4}^{\ast },L_{1},L_{2}}(Y_{1},Y_{2}) & = & \displaystyle 2^{1+2\unicode[STIX]{x1D6FD}}C(n_{1},\unicode[STIX]{x1D702}_{1},n_{2},\unicode[STIX]{x1D702}_{2})\mathop{\sum }_{\unicode[STIX]{x1D6FE}_{1}\in \unicode[STIX]{x1D6E4}_{\unicode[STIX]{x1D702}_{1}}^{\ast }}\mathop{\sum }_{\unicode[STIX]{x1D6FE}_{2}\in \unicode[STIX]{x1D6E4}_{\unicode[STIX]{x1D702}_{2}}^{\ast }}\unicode[STIX]{x1D70E}^{\ast }(\unicode[STIX]{x1D6FE})^{-1}C(\unicode[STIX]{x1D6FE},L_{2})\nonumber\\ \displaystyle & & \displaystyle \times \,\int _{A(\unicode[STIX]{x1D6FE}_{1})}\mathop{\sum }_{e_{1}\in {\mathcal{E}}_{1},u_{1}\in {\mathcal{U}}_{1}}\hat{i} _{\operatorname{iso}}[a_{1},e_{1},u_{1}](Y_{1})\,da_{1}\nonumber\\ \displaystyle & & \displaystyle \times \,\int _{A(\unicode[STIX]{x1D6FE}_{2})}\mathop{\sum }_{e_{2}\in {\mathcal{E}}_{2},u_{2}\in {\mathcal{U}}_{2}}\hat{i} _{\operatorname{iso}}[a_{2},e_{2},u_{2}](Y_{2})\,da_{2}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle {\mathcal{J}}_{\unicode[STIX]{x1D6E4}^{\ast },L_{1},L_{2}}(Y_{1},Y_{2}) & = & \displaystyle 2^{1+2\unicode[STIX]{x1D6FD}}C(n_{1},\unicode[STIX]{x1D702}_{1},n_{2},\unicode[STIX]{x1D702}_{2})\mathop{\sum }_{\unicode[STIX]{x1D6FE}_{1}\in \unicode[STIX]{x1D6E4}_{\unicode[STIX]{x1D702}_{1}}^{\ast }}\mathop{\sum }_{\unicode[STIX]{x1D6FE}_{2}\in \unicode[STIX]{x1D6E4}_{\unicode[STIX]{x1D702}_{2}}^{\ast }}\unicode[STIX]{x1D70E}^{\ast }(\unicode[STIX]{x1D6FE})^{-1}C(\unicode[STIX]{x1D6FE},L_{2})\nonumber\\ \displaystyle & & \displaystyle \times \,\int _{A(\unicode[STIX]{x1D6FE}_{1})}\mathop{\sum }_{e_{1}\in {\mathcal{E}}_{1},u_{1}\in {\mathcal{U}}_{1}}\hat{i} _{\operatorname{iso}}[a_{1},e_{1},u_{1}](Y_{1})\,da_{1}\nonumber\\ \displaystyle & & \displaystyle \times \,\int _{A(\unicode[STIX]{x1D6FE}_{2})}\mathop{\sum }_{e_{2}\in {\mathcal{E}}_{2},u_{2}\in {\mathcal{U}}_{2}}\hat{i} _{\operatorname{iso}}[a_{2},e_{2},u_{2}](Y_{2})\,da_{2}.\nonumber\end{eqnarray}$$
Soit
![]() $\unicode[STIX]{x1D6FE}_{1}$
,
$\unicode[STIX]{x1D6FE}_{1}$
,
![]() $\unicode[STIX]{x1D6FE}_{2}$
et
$\unicode[STIX]{x1D6FE}_{2}$
et
![]() $\unicode[STIX]{x1D6FE}$
intervenant dans cette formule. Rappelons la définition
$\unicode[STIX]{x1D6FE}$
intervenant dans cette formule. Rappelons la définition
Posons
En vertu de (7), on a
Alors la formule précédente devient
 $$\begin{eqnarray}\displaystyle {\mathcal{J}}_{\unicode[STIX]{x1D6E4}^{\ast },L_{1},L_{2}}(Y_{1},Y_{2}) & = & \displaystyle C_{4}2^{1+\unicode[STIX]{x1D6FD}-2t_{1}^{\prime }-2t_{2}^{\prime }}C(w^{\prime })C(w^{\prime \prime })\unicode[STIX]{x1D6FC}(t_{1}^{\prime },w^{\prime },\unicode[STIX]{x1D702}_{1})\unicode[STIX]{x1D6FC}(t_{2}^{\prime },w^{\prime \prime },\unicode[STIX]{x1D702}_{2})\nonumber\\ \displaystyle & & \displaystyle \times \,\mathop{\sum }_{\unicode[STIX]{x1D6FE}_{1}\in \unicode[STIX]{x1D6E4}_{\unicode[STIX]{x1D702}_{1}}^{\ast }}\unicode[STIX]{x1D70E}(\unicode[STIX]{x1D6FE}_{1})\int _{A(\unicode[STIX]{x1D6FE}_{1})}\mathop{\sum }_{e_{1}\in {\mathcal{E}}_{1},u_{1}\in {\mathcal{U}}_{1}}\hat{i} _{\operatorname{iso}}[a_{1},e_{1},u_{1}](Y_{1})\,da_{1}\nonumber\\ \displaystyle & & \displaystyle \times \,\mathop{\sum }_{\unicode[STIX]{x1D6FE}_{2}\in \unicode[STIX]{x1D6E4}_{\unicode[STIX]{x1D702}_{2}}^{\ast }}\unicode[STIX]{x1D70E}(\unicode[STIX]{x1D6FE}_{2})\int _{A(\unicode[STIX]{x1D6FE}_{2})}\mathop{\sum }_{e_{2}\in {\mathcal{E}}_{2},u_{2}\in {\mathcal{U}}_{2}}\hat{i} _{\operatorname{iso}}[a_{2},e_{2},u_{2}](Y_{2})\,da_{2}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle {\mathcal{J}}_{\unicode[STIX]{x1D6E4}^{\ast },L_{1},L_{2}}(Y_{1},Y_{2}) & = & \displaystyle C_{4}2^{1+\unicode[STIX]{x1D6FD}-2t_{1}^{\prime }-2t_{2}^{\prime }}C(w^{\prime })C(w^{\prime \prime })\unicode[STIX]{x1D6FC}(t_{1}^{\prime },w^{\prime },\unicode[STIX]{x1D702}_{1})\unicode[STIX]{x1D6FC}(t_{2}^{\prime },w^{\prime \prime },\unicode[STIX]{x1D702}_{2})\nonumber\\ \displaystyle & & \displaystyle \times \,\mathop{\sum }_{\unicode[STIX]{x1D6FE}_{1}\in \unicode[STIX]{x1D6E4}_{\unicode[STIX]{x1D702}_{1}}^{\ast }}\unicode[STIX]{x1D70E}(\unicode[STIX]{x1D6FE}_{1})\int _{A(\unicode[STIX]{x1D6FE}_{1})}\mathop{\sum }_{e_{1}\in {\mathcal{E}}_{1},u_{1}\in {\mathcal{U}}_{1}}\hat{i} _{\operatorname{iso}}[a_{1},e_{1},u_{1}](Y_{1})\,da_{1}\nonumber\\ \displaystyle & & \displaystyle \times \,\mathop{\sum }_{\unicode[STIX]{x1D6FE}_{2}\in \unicode[STIX]{x1D6E4}_{\unicode[STIX]{x1D702}_{2}}^{\ast }}\unicode[STIX]{x1D70E}(\unicode[STIX]{x1D6FE}_{2})\int _{A(\unicode[STIX]{x1D6FE}_{2})}\mathop{\sum }_{e_{2}\in {\mathcal{E}}_{2},u_{2}\in {\mathcal{U}}_{2}}\hat{i} _{\operatorname{iso}}[a_{2},e_{2},u_{2}](Y_{2})\,da_{2}.\nonumber\end{eqnarray}$$
Autrement dit, en utilisant (6) et son analogue pour l’indice
![]() $2$
:
$2$
:
Cette expression ne dépend ni de
![]() $\unicode[STIX]{x1D6E4}^{\ast }$
, ni de
$\unicode[STIX]{x1D6E4}^{\ast }$
, ni de
![]() $L_{1}$
et
$L_{1}$
et
![]() $L_{2}$
. Reportons cette valeur dans l’égalité (5). La somme en
$L_{2}$
. Reportons cette valeur dans l’égalité (5). La somme en
![]() $(L_{1},L_{2})$
, pondérée par
$(L_{1},L_{2})$
, pondérée par
![]() $|{\mathcal{L}}|^{-1}$
, disparaît. La somme en
$|{\mathcal{L}}|^{-1}$
, disparaît. La somme en
![]() $\unicode[STIX]{x1D6E4}^{\ast }$
se transforme en la multiplication par
$\unicode[STIX]{x1D6E4}^{\ast }$
se transforme en la multiplication par
![]() $|\boldsymbol{\unicode[STIX]{x1D6E4}}|$
. Enfin, la somme en
$|\boldsymbol{\unicode[STIX]{x1D6E4}}|$
. Enfin, la somme en
![]() $(Y_{1},Y_{2})$
remplace les intégrales orbitales par leurs versions stables. D’où
$(Y_{1},Y_{2})$
remplace les intégrales orbitales par leurs versions stables. D’où
Considérons le cas de l’indice
![]() $1$
. Le quadruplet
$1$
. Le quadruplet
![]() $(t_{1}^{\prime },t_{1}^{\prime \prime },N^{\prime },0)$
vérifie l’hypothèse du (i) du théorème 3.20 de [Reference Moeglin and Waldspurger6]. Donc
$(t_{1}^{\prime },t_{1}^{\prime \prime },N^{\prime },0)$
vérifie l’hypothèse du (i) du théorème 3.20 de [Reference Moeglin and Waldspurger6]. Donc
![]() $f_{1}$
est stable au sens de cette référence. On sait de plus que le nombre de classes de conjugaison dans la classe de conjugaison stable de
$f_{1}$
est stable au sens de cette référence. On sait de plus que le nombre de classes de conjugaison dans la classe de conjugaison stable de
![]() $\bar{Y}_{1}$
est égal à celui des classes de conjugaison dans la classe de conjugaison stable dans
$\bar{Y}_{1}$
est égal à celui des classes de conjugaison dans la classe de conjugaison stable dans
![]() $\mathfrak{g}_{n_{1},\unicode[STIX]{x1D702}_{1},\operatorname{an}}(F)$
correspondant à celle de
$\mathfrak{g}_{n_{1},\unicode[STIX]{x1D702}_{1},\operatorname{an}}(F)$
correspondant à celle de
![]() $\bar{Y}_{1}$
. D’où
$\bar{Y}_{1}$
. D’où
Une fois de plus, cette égalité n’est vraie que si
![]() $n_{1}\not =0$
. Si
$n_{1}\not =0$
. Si
![]() $n_{1}=0$
, le terme
$n_{1}=0$
, le terme
![]() $\frac{1}{2}$
disparaît. Le produit de ces constantes sur les indices
$\frac{1}{2}$
disparaît. Le produit de ces constantes sur les indices
![]() $1$
et
$1$
et
![]() $2$
vaut donc
$2$
vaut donc
![]() $2^{-1-\unicode[STIX]{x1D6FD}}$
. D’où l’égalité
$2^{-1-\unicode[STIX]{x1D6FD}}$
. D’où l’égalité
Cela étant vrai pour tout couple
![]() $(\bar{Y}_{1},\bar{Y}_{2})$
, cela démontre que
$(\bar{Y}_{1},\bar{Y}_{2})$
, cela démontre que
Pour obtenir l’assertion (i) du lemme 2.2, il reste à démontrer l’égalité
Il suffit pour cela de reprendre les définitions de toutes nos constantes. On laisse ce calcul pénible mais sans mystère au lecteur. ◻
3 Démonstration de la proposition 1.2
3.1 Descente du facteur de transfert
On revient à nos deux groupes
![]() $G_{\operatorname{iso}}$
et
$G_{\operatorname{iso}}$
et
![]() $G_{\operatorname{an}}$
du paragraphe 1. On dit qu’un élément
$G_{\operatorname{an}}$
du paragraphe 1. On dit qu’un élément
![]() $u\in G_{\sharp }(F)$
est topologiquement unipotent si ses valeurs propres, qui appartiennent à une certaine extension finie
$u\in G_{\sharp }(F)$
est topologiquement unipotent si ses valeurs propres, qui appartiennent à une certaine extension finie
![]() $F^{\prime }$
de
$F^{\prime }$
de
![]() $F$
, sont congrues à
$F$
, sont congrues à
![]() $1$
modulo l’idéal maximal de l’anneau des entiers de
$1$
modulo l’idéal maximal de l’anneau des entiers de
![]() $F^{\prime }$
. L’application
$F^{\prime }$
. L’application
![]() $E:X\mapsto E(X)=(1+X/2)(1-X/2)$
est une bijection entre l’ensemble des éléments
$E:X\mapsto E(X)=(1+X/2)(1-X/2)$
est une bijection entre l’ensemble des éléments
![]() $X\in \mathfrak{g}_{\sharp }(F)$
topologiquement nilpotents et l’ensemble des éléments topologiquement unipotents de
$X\in \mathfrak{g}_{\sharp }(F)$
topologiquement nilpotents et l’ensemble des éléments topologiquement unipotents de
![]() $G_{\sharp }(F)$
.
$G_{\sharp }(F)$
.
Soit
![]() $\sharp =\operatorname{iso}$
ou
$\sharp =\operatorname{iso}$
ou
![]() $\operatorname{an}$
et soit
$\operatorname{an}$
et soit
![]() $x\in G_{\sharp }(F)$
un élément elliptique et fortement régulier. On peut décomposer
$x\in G_{\sharp }(F)$
un élément elliptique et fortement régulier. On peut décomposer
![]() $x$
en un unique produit
$x$
en un unique produit
![]() $x=su$
, où
$x=su$
, où
![]() $s$
et
$s$
et
![]() $u$
commutent entre eux,
$u$
commutent entre eux,
![]() $s$
est un élément dont toutes les valeurs propres sont des racines de l’unité d’ordre premier à
$s$
est un élément dont toutes les valeurs propres sont des racines de l’unité d’ordre premier à
![]() $p$
et
$p$
et
![]() $u$
est topologiquement unipotent. Au lieu de
$u$
est topologiquement unipotent. Au lieu de
![]() $u$
, on considère plutôt l’élément topologiquement nilpotent de
$u$
, on considère plutôt l’élément topologiquement nilpotent de
![]() $X\in \mathfrak{g}_{\sharp }(F)$
tel que
$X\in \mathfrak{g}_{\sharp }(F)$
tel que
![]() $u=E(X)$
. On écrit donc
$u=E(X)$
. On écrit donc
![]() $x=sE(X)$
. Parmi les valeurs propres de
$x=sE(X)$
. Parmi les valeurs propres de
![]() $s$
, on distingue le nombre
$s$
, on distingue le nombre
![]() $1$
qui intervient avec une multiplicité impaire notée
$1$
qui intervient avec une multiplicité impaire notée
![]() $1+2n_{+}$
et le nombre
$1+2n_{+}$
et le nombre
![]() $-1$
qui intervient avec une multiplicité paire notée
$-1$
qui intervient avec une multiplicité paire notée
![]() $2n_{-}$
(qui peut être nulle). On note
$2n_{-}$
(qui peut être nulle). On note
![]() $V_{+}$
et
$V_{+}$
et
![]() $V_{-}$
les espaces propres associés,
$V_{-}$
les espaces propres associés,
![]() $Q_{+}$
et
$Q_{+}$
et
![]() $Q_{-}$
les restrictions de
$Q_{-}$
les restrictions de
![]() $Q_{\sharp }$
à ces espaces et on pose
$Q_{\sharp }$
à ces espaces et on pose
![]() $\unicode[STIX]{x1D702}_{+}=\unicode[STIX]{x1D702}(Q_{+})$
et
$\unicode[STIX]{x1D702}_{+}=\unicode[STIX]{x1D702}(Q_{+})$
et
![]() $\unicode[STIX]{x1D702}_{-}=\unicode[STIX]{x1D702}(Q_{-})$
. On note
$\unicode[STIX]{x1D702}_{-}=\unicode[STIX]{x1D702}(Q_{-})$
. On note
![]() $G_{+}=\operatorname{SO}(Q_{+})$
,
$G_{+}=\operatorname{SO}(Q_{+})$
,
![]() $G_{-}=\operatorname{SO}(Q_{-})$
. Le groupe de Galois
$G_{-}=\operatorname{SO}(Q_{-})$
. Le groupe de Galois
![]() $\operatorname{Gal}(\bar{F}/F)$
agit sur l’ensemble des valeurs propres de
$\operatorname{Gal}(\bar{F}/F)$
agit sur l’ensemble des valeurs propres de
![]() $s$
différentes de
$s$
différentes de
![]() $\pm 1$
, en préservant leurs multiplicités. Notons
$\pm 1$
, en préservant leurs multiplicités. Notons
![]() $I$
l’ensemble des orbites. Soit
$I$
l’ensemble des orbites. Soit
![]() $i\in I$
, fixons un élément
$i\in I$
, fixons un élément
![]() $s_{i}$
de cette orbite et notons
$s_{i}$
de cette orbite et notons
![]() $d_{i}$
sa multiplicité. Posons
$d_{i}$
sa multiplicité. Posons
![]() $E_{i}=F[s_{i}]$
. C’est une extension non ramifiée de
$E_{i}=F[s_{i}]$
. C’est une extension non ramifiée de
![]() $F$
. Parce que
$F$
. Parce que
![]() $s$
appartient à un groupe orthogonal, il existe une sous-extension
$s$
appartient à un groupe orthogonal, il existe une sous-extension
![]() $E_{i}^{\natural }$
de
$E_{i}^{\natural }$
de
![]() $F$
telle que
$F$
telle que
![]() $[E_{i}:E_{i}^{\natural }]=2$
et
$[E_{i}:E_{i}^{\natural }]=2$
et
![]() $\operatorname{norme}_{E_{i}/E_{i}^{\natural }}(s_{i})=1$
. Notons
$\operatorname{norme}_{E_{i}/E_{i}^{\natural }}(s_{i})=1$
. Notons
![]() $V_{i}$
la somme des espaces propres associés à des valeurs propres conjuguées de
$V_{i}$
la somme des espaces propres associés à des valeurs propres conjuguées de
![]() $s_{i}$
et notons
$s_{i}$
et notons
![]() $s_{|V_{i}}$
la restriction de
$s_{|V_{i}}$
la restriction de
![]() $s$
à cet espace. L’algèbre
$s$
à cet espace. L’algèbre
![]() $F[s_{|V_{i}}]$
s’identifie à
$F[s_{|V_{i}}]$
s’identifie à
![]() $E_{i}$
par
$E_{i}$
par
![]() $s_{|V_{i}}\mapsto s_{i}$
. Puisque
$s_{|V_{i}}\mapsto s_{i}$
. Puisque
![]() $V_{i}$
est naturellement un
$V_{i}$
est naturellement un
![]() $F[s_{|V_{i}}]$
-module, il devient un
$F[s_{|V_{i}}]$
-module, il devient un
![]() $E_{i}$
-espace vectoriel, dont la dimension est
$E_{i}$
-espace vectoriel, dont la dimension est
![]() $d_{i}$
. On montre qu’il existe une unique forme hermitienne non dégénérée
$d_{i}$
. On montre qu’il existe une unique forme hermitienne non dégénérée
![]() $Q_{i}$
sur
$Q_{i}$
sur
![]() $V_{i}$
(relative à l’extension
$V_{i}$
(relative à l’extension
![]() $E_{i}/E_{i}^{\natural }$
) de sorte que, pour tous
$E_{i}/E_{i}^{\natural }$
) de sorte que, pour tous
![]() $v,v^{\prime }\in V_{i}$
, on ait l’égalité
$v,v^{\prime }\in V_{i}$
, on ait l’égalité
Notons
![]() $G_{i}$
le groupe unitaire de
$G_{i}$
le groupe unitaire de
![]() $Q_{i}$
. La composante neutre
$Q_{i}$
. La composante neutre
![]() $G_{s}$
du commutant de
$G_{s}$
du commutant de
![]() $s$
dans
$s$
dans
![]() $G_{\sharp }$
est le groupe
$G_{\sharp }$
est le groupe
On a
![]() $X\in \mathfrak{g}_{s}(F)$
. C’est un élément elliptique régulier.
$X\in \mathfrak{g}_{s}(F)$
. C’est un élément elliptique régulier.
Remarques.
(1) La condition d’ellipticité empêche le couple
 $(n_{-},\unicode[STIX]{x1D702}_{-})$
d’être égal à
$(n_{-},\unicode[STIX]{x1D702}_{-})$
d’être égal à
 $(1,1)$
.
$(1,1)$
.(2) Fixons un élément
 $\unicode[STIX]{x1D709}\in \mathfrak{o}^{\times }-\mathfrak{o}^{\times 2}$
. Pour
$\unicode[STIX]{x1D709}\in \mathfrak{o}^{\times }-\mathfrak{o}^{\times 2}$
. Pour
 $i\in I$
, notons
$i\in I$
, notons
 $Q_{\sharp ,|V_{i}}$
la restriction de
$Q_{\sharp ,|V_{i}}$
la restriction de
 $Q_{\sharp }$
à
$Q_{\sharp }$
à
 $V_{i}$
. On calcule facilement
$V_{i}$
. On calcule facilement
 $\unicode[STIX]{x1D702}(Q_{\sharp ,|V_{i}})=\unicode[STIX]{x1D709}^{d_{i}}$
. Parce que l’on a supposé que
$\unicode[STIX]{x1D702}(Q_{\sharp ,|V_{i}})=\unicode[STIX]{x1D709}^{d_{i}}$
. Parce que l’on a supposé que
 $\unicode[STIX]{x1D702}(Q_{\sharp })=1$
, on en déduit l’égalité où
$\unicode[STIX]{x1D702}(Q_{\sharp })=1$
, on en déduit l’égalité où $$\begin{eqnarray}\unicode[STIX]{x1D702}_{+}\unicode[STIX]{x1D702}_{-}\unicode[STIX]{x1D709}^{d}=1,\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D702}_{+}\unicode[STIX]{x1D702}_{-}\unicode[STIX]{x1D709}^{d}=1,\end{eqnarray}$$
 $d=\sum _{i\in I}d_{i}$
.
$d=\sum _{i\in I}d_{i}$
.
Si l’on écrit
![]() $X=(X_{+},X_{-},(X_{i})_{i\in I})$
, on définit la classe totale de conjugaison stable de
$X=(X_{+},X_{-},(X_{i})_{i\in I})$
, on définit la classe totale de conjugaison stable de
![]() $X_{+}$
,
$X_{+}$
,
![]() $X_{-}$
et
$X_{-}$
et
![]() $X_{i}$
pour
$X_{i}$
pour
![]() $i\in I$
de la même façon qu’en 1.2. On définit la classe totale de conjugaison stable de
$i\in I$
de la même façon qu’en 1.2. On définit la classe totale de conjugaison stable de
![]() $X$
comme le produit de ces classes.
$X$
comme le produit de ces classes.
Considérons maintenant un élément
![]() $x^{\prime }$
dans la classe totale de conjugaison stable de
$x^{\prime }$
dans la classe totale de conjugaison stable de
![]() $x$
. Il se décompose en
$x$
. Il se décompose en
![]() $x^{\prime }=s^{\prime }E(X^{\prime })$
. Les données
$x^{\prime }=s^{\prime }E(X^{\prime })$
. Les données
![]() $n_{+}$
,
$n_{+}$
,
![]() $\unicode[STIX]{x1D702}_{+}$
,
$\unicode[STIX]{x1D702}_{+}$
,
![]() $n_{-}$
,
$n_{-}$
,
![]() $\unicode[STIX]{x1D702}_{-}$
,
$\unicode[STIX]{x1D702}_{-}$
,
![]() $I$
et
$I$
et
![]() $d_{i}$
ne changent pas quand on remplace
$d_{i}$
ne changent pas quand on remplace
![]() $s$
par
$s$
par
![]() $s^{\prime }$
. Les formes
$s^{\prime }$
. Les formes
![]() $Q_{+}$
,
$Q_{+}$
,
![]() $Q_{-}$
et
$Q_{-}$
et
![]() $Q_{i}$
pour
$Q_{i}$
pour
![]() $i\in I$
peuvent changer. Par exemple, soit
$i\in I$
peuvent changer. Par exemple, soit
![]() $Q_{+}^{\prime }$
la forme remplaçant
$Q_{+}^{\prime }$
la forme remplaçant
![]() $Q_{+}$
. Ou bien
$Q_{+}$
. Ou bien
![]() $Q_{+}^{\prime }$
est isomorphe à
$Q_{+}^{\prime }$
est isomorphe à
![]() $Q_{+}$
, ou bien le couple
$Q_{+}$
, ou bien le couple
![]() $(Q_{+}^{\prime },Q_{+})$
est égal, à l’ordre près, à l’un de nos couples
$(Q_{+}^{\prime },Q_{+})$
est égal, à l’ordre près, à l’un de nos couples
![]() $(Q_{\operatorname{iso}},Q_{\operatorname{an}})$
du paragraphe 2.1. On voit qu’à la classe de conjugaison stable de
$(Q_{\operatorname{iso}},Q_{\operatorname{an}})$
du paragraphe 2.1. On voit qu’à la classe de conjugaison stable de
![]() $X$
dans
$X$
dans
![]() $\mathfrak{g}_{s}(F)$
correspond une classe de conjugaison stable dans
$\mathfrak{g}_{s}(F)$
correspond une classe de conjugaison stable dans
![]() $\mathfrak{g}_{s^{\prime }}(F)$
. L’élément
$\mathfrak{g}_{s^{\prime }}(F)$
. L’élément
![]() $X^{\prime }$
appartient à cette classe, autrement dit,
$X^{\prime }$
appartient à cette classe, autrement dit,
![]() $X^{\prime }$
appartient à la classe totale de conjugaison stable de
$X^{\prime }$
appartient à la classe totale de conjugaison stable de
![]() $X$
. Plus précisément, l’application
$X$
. Plus précisément, l’application
![]() $x^{\prime }\mapsto X^{\prime }$
se quotiente en une bijection entre l’ensemble des classes de conjugaison contenues dans la classe totale de conjugaison stable de
$x^{\prime }\mapsto X^{\prime }$
se quotiente en une bijection entre l’ensemble des classes de conjugaison contenues dans la classe totale de conjugaison stable de
![]() $x$
et l’ensemble des classes de conjugaison contenues dans la classe totale de conjugaison stable de
$x$
et l’ensemble des classes de conjugaison contenues dans la classe totale de conjugaison stable de
![]() $X$
.
$X$
.
Comme on vient de le dire,
![]() $Q_{+}$
est l’une des formes
$Q_{+}$
est l’une des formes
![]() $Q_{\operatorname{iso}}$
ou
$Q_{\operatorname{iso}}$
ou
![]() $Q_{\operatorname{an}}$
de 2.1. Posons
$Q_{\operatorname{an}}$
de 2.1. Posons
![]() $\operatorname{sgn}^{\ast }(X_{+})=1$
si c’est
$\operatorname{sgn}^{\ast }(X_{+})=1$
si c’est
![]() $Q_{\operatorname{iso}}$
et
$Q_{\operatorname{iso}}$
et
![]() $\operatorname{sgn}^{\ast }(X_{+})=-1$
si c’est
$\operatorname{sgn}^{\ast }(X_{+})=-1$
si c’est
![]() $Q_{\operatorname{an}}$
. On définit de même
$Q_{\operatorname{an}}$
. On définit de même
![]() $\operatorname{sgn}^{\ast }(X_{-})$
et
$\operatorname{sgn}^{\ast }(X_{-})$
et
![]() $\operatorname{sgn}^{\ast }(X_{i})$
pour
$\operatorname{sgn}^{\ast }(X_{i})$
pour
![]() $i\in I$
. On pose
$i\in I$
. On pose
On rappelle que, pour notre indice
![]() $\sharp$
fixé plus haut, on a défini
$\sharp$
fixé plus haut, on a défini
![]() $\operatorname{sgn}_{\sharp }=1$
si
$\operatorname{sgn}_{\sharp }=1$
si
![]() $\sharp =iso$
et
$\sharp =iso$
et
![]() $\operatorname{sgn}_{\sharp }=-1$
si
$\operatorname{sgn}_{\sharp }=-1$
si
![]() $\sharp =an$
. Montrons que
$\sharp =an$
. Montrons que
(3) on a l’égalité
Preuve.
Dans chacun de nos espaces
![]() $V_{+}$
,
$V_{+}$
,
![]() $V_{-}$
et
$V_{-}$
et
![]() $V_{i}$
pour
$V_{i}$
pour
![]() $i\in I$
, on fixe un réseau presque autodual (cf. [Reference Waldspurger11] 1.1) que l’on note respectivement
$i\in I$
, on fixe un réseau presque autodual (cf. [Reference Waldspurger11] 1.1) que l’on note respectivement
![]() $L_{+}$
,
$L_{+}$
,
![]() $L_{-}$
et
$L_{-}$
et
![]() $L_{i}$
. On note
$L_{i}$
. On note
![]() $L$
la somme directe de ces réseaux. C’est un réseau presque autodual de
$L$
la somme directe de ces réseaux. C’est un réseau presque autodual de
![]() $V_{\sharp }$
. On pose
$V_{\sharp }$
. On pose
![]() $l_{+}^{\prime \prime }=L_{+}^{\ast }/L_{+}$
et on définit de même
$l_{+}^{\prime \prime }=L_{+}^{\ast }/L_{+}$
et on définit de même
![]() $l_{-}^{\prime \prime }$
,
$l_{-}^{\prime \prime }$
,
![]() $l_{i}^{\prime \prime }$
et
$l_{i}^{\prime \prime }$
et
![]() $l^{\prime \prime }$
. Chacun de ces espaces est muni d’une forme quadratique dont l’on note les déterminants normalisés
$l^{\prime \prime }$
. Chacun de ces espaces est muni d’une forme quadratique dont l’on note les déterminants normalisés
![]() $\unicode[STIX]{x1D702}_{+}^{\prime \prime }$
,
$\unicode[STIX]{x1D702}_{+}^{\prime \prime }$
,
![]() $\unicode[STIX]{x1D702}_{-}^{\prime \prime }$
,
$\unicode[STIX]{x1D702}_{-}^{\prime \prime }$
,
![]() $\unicode[STIX]{x1D702}_{i}^{\prime \prime }$
et
$\unicode[STIX]{x1D702}_{i}^{\prime \prime }$
et
![]() $\unicode[STIX]{x1D702}^{\prime \prime }$
(rappelons que, par exemple,
$\unicode[STIX]{x1D702}^{\prime \prime }$
(rappelons que, par exemple,
![]() $\unicode[STIX]{x1D702}^{\prime \prime }$
est le produit du déterminant habituel par
$\unicode[STIX]{x1D702}^{\prime \prime }$
est le produit du déterminant habituel par
![]() $(-1)^{[\operatorname{dim}_{\mathbb{F}_{q}}(l^{\prime \prime })/2]}$
). Par définition de
$(-1)^{[\operatorname{dim}_{\mathbb{F}_{q}}(l^{\prime \prime })/2]}$
). Par définition de
![]() $V_{\sharp }$
, la dimension de
$V_{\sharp }$
, la dimension de
![]() $l^{\prime \prime }$
sur
$l^{\prime \prime }$
sur
![]() $\mathbb{F}_{q}$
est paire et l’on a
$\mathbb{F}_{q}$
est paire et l’on a
![]() $\operatorname{sgn}_{\sharp }=\operatorname{sgn}(\unicode[STIX]{x1D702}^{\prime \prime })$
. On vérifie facilement que, pour
$\operatorname{sgn}_{\sharp }=\operatorname{sgn}(\unicode[STIX]{x1D702}^{\prime \prime })$
. On vérifie facilement que, pour
![]() $i\in I$
, la dimension de
$i\in I$
, la dimension de
![]() $l_{i}^{\prime \prime }$
est paire. D’après la définition de [Reference Waldspurger11] 1.1, on a
$l_{i}^{\prime \prime }$
est paire. D’après la définition de [Reference Waldspurger11] 1.1, on a
![]() $\operatorname{sgn}^{\ast }(X_{i})=\operatorname{sgn}(\unicode[STIX]{x1D702}_{i}^{\prime \prime })$
. Supposons
$\operatorname{sgn}^{\ast }(X_{i})=\operatorname{sgn}(\unicode[STIX]{x1D702}_{i}^{\prime \prime })$
. Supposons
![]() $\operatorname{val}_{F}(\unicode[STIX]{x1D702}_{+})$
paire. Le terme
$\operatorname{val}_{F}(\unicode[STIX]{x1D702}_{+})$
paire. Le terme
![]() $\operatorname{val}_{F}(\unicode[STIX]{x1D702}_{-})$
est également pair d’après (2). Alors les dimensions de
$\operatorname{val}_{F}(\unicode[STIX]{x1D702}_{-})$
est également pair d’après (2). Alors les dimensions de
![]() $l_{+}^{\prime \prime }$
et
$l_{+}^{\prime \prime }$
et
![]() $l_{-}^{\prime \prime }$
sont paires et l’on a
$l_{-}^{\prime \prime }$
sont paires et l’on a
![]() $\operatorname{sgn}^{\ast }(X_{+})=\operatorname{sgn}(\unicode[STIX]{x1D702}_{+}^{\prime \prime })$
,
$\operatorname{sgn}^{\ast }(X_{+})=\operatorname{sgn}(\unicode[STIX]{x1D702}_{+}^{\prime \prime })$
,
![]() $\operatorname{sgn}^{\ast }(X_{-})=\operatorname{sgn}(\unicode[STIX]{x1D702}_{-}^{\prime \prime })$
. Le déterminant non normalisé de la forme sur
$\operatorname{sgn}^{\ast }(X_{-})=\operatorname{sgn}(\unicode[STIX]{x1D702}_{-}^{\prime \prime })$
. Le déterminant non normalisé de la forme sur
![]() $l^{\prime \prime }$
est le produit des déterminants non normalisés des formes sur
$l^{\prime \prime }$
est le produit des déterminants non normalisés des formes sur
![]() $l_{+}^{\prime \prime }$
,
$l_{+}^{\prime \prime }$
,
![]() $l_{-}^{\prime \prime }$
et
$l_{-}^{\prime \prime }$
et
![]() $l_{i}^{\prime \prime }$
pour
$l_{i}^{\prime \prime }$
pour
![]() $i\in I$
. Puisque toutes les dimensions sont paires, il en est de même des déterminants normalisés : on a
$i\in I$
. Puisque toutes les dimensions sont paires, il en est de même des déterminants normalisés : on a
![]() $\unicode[STIX]{x1D702}^{\prime \prime }=\unicode[STIX]{x1D702}_{+}^{\prime \prime }\unicode[STIX]{x1D702}_{-}^{\prime \prime }\prod _{i\in I}\unicode[STIX]{x1D702}_{i}^{\prime \prime }$
. Avec les formules ci-dessus, on obtient
$\unicode[STIX]{x1D702}^{\prime \prime }=\unicode[STIX]{x1D702}_{+}^{\prime \prime }\unicode[STIX]{x1D702}_{-}^{\prime \prime }\prod _{i\in I}\unicode[STIX]{x1D702}_{i}^{\prime \prime }$
. Avec les formules ci-dessus, on obtient
ce qui coïncide avec (3) puisque
![]() $\operatorname{val}_{F}(\unicode[STIX]{x1D702}_{-})$
est paire. Supposons maintenant
$\operatorname{val}_{F}(\unicode[STIX]{x1D702}_{-})$
est paire. Supposons maintenant
![]() $\operatorname{val}_{F}(\unicode[STIX]{x1D702}_{+})$
impaire, donc
$\operatorname{val}_{F}(\unicode[STIX]{x1D702}_{+})$
impaire, donc
![]() $\operatorname{val}_{F}(\unicode[STIX]{x1D702}_{-})$
aussi impaire. Alors les dimensions de
$\operatorname{val}_{F}(\unicode[STIX]{x1D702}_{-})$
aussi impaire. Alors les dimensions de
![]() $l_{+}^{\prime \prime }$
et
$l_{+}^{\prime \prime }$
et
![]() $l_{-}^{\prime \prime }$
sont impaires. D’après les définitions de [Reference Waldspurger11] 1.1, on a
$l_{-}^{\prime \prime }$
sont impaires. D’après les définitions de [Reference Waldspurger11] 1.1, on a
![]() $\operatorname{sgn}^{\ast }(X_{+})=\operatorname{sgn}(\unicode[STIX]{x1D702}_{+}^{\prime })$
et
$\operatorname{sgn}^{\ast }(X_{+})=\operatorname{sgn}(\unicode[STIX]{x1D702}_{+}^{\prime })$
et
![]() $\operatorname{sgn}^{\ast }(X_{-})=\operatorname{sgn}(\unicode[STIX]{x1D702}_{-}^{\prime })$
, où
$\operatorname{sgn}^{\ast }(X_{-})=\operatorname{sgn}(\unicode[STIX]{x1D702}_{-}^{\prime })$
, où
![]() $\unicode[STIX]{x1D702}_{+}^{\prime }$
et
$\unicode[STIX]{x1D702}_{+}^{\prime }$
et
![]() $\unicode[STIX]{x1D702}_{-}^{\prime }$
sont les déterminants normalisés des formes quadratiques sur
$\unicode[STIX]{x1D702}_{-}^{\prime }$
sont les déterminants normalisés des formes quadratiques sur
![]() $L_{+}/\unicode[STIX]{x1D71B}L_{+}^{\ast }$
et
$L_{+}/\unicode[STIX]{x1D71B}L_{+}^{\ast }$
et
![]() $L_{-}/\unicode[STIX]{x1D71B}L_{-}^{\ast }$
. Parce que la dimension de
$L_{-}/\unicode[STIX]{x1D71B}L_{-}^{\ast }$
. Parce que la dimension de
![]() $V_{+}$
est impaire et que celle de
$V_{+}$
est impaire et que celle de
![]() $V_{-}$
est paire, on a
$V_{-}$
est paire, on a
![]() $\unicode[STIX]{x1D702}_{+}^{\prime }\unicode[STIX]{x1D702}_{+}^{\prime \prime }=\unicode[STIX]{x1D702}_{+}\unicode[STIX]{x1D71B}^{-\operatorname{val}_{F}(\unicode[STIX]{x1D702}_{+})}$
et
$\unicode[STIX]{x1D702}_{+}^{\prime }\unicode[STIX]{x1D702}_{+}^{\prime \prime }=\unicode[STIX]{x1D702}_{+}\unicode[STIX]{x1D71B}^{-\operatorname{val}_{F}(\unicode[STIX]{x1D702}_{+})}$
et
![]() $\unicode[STIX]{x1D702}_{-}^{\prime }\unicode[STIX]{x1D702}_{-}^{\prime \prime }=-\unicode[STIX]{x1D702}_{-}\unicode[STIX]{x1D71B}^{-\operatorname{val}_{F}(\unicode[STIX]{x1D702}_{-})}$
. Parce que
$\unicode[STIX]{x1D702}_{-}^{\prime }\unicode[STIX]{x1D702}_{-}^{\prime \prime }=-\unicode[STIX]{x1D702}_{-}\unicode[STIX]{x1D71B}^{-\operatorname{val}_{F}(\unicode[STIX]{x1D702}_{-})}$
. Parce que
![]() $l_{+}^{\prime \prime }$
et
$l_{+}^{\prime \prime }$
et
![]() $l_{-}^{\prime \prime }$
sont de dimension impaire, on voit qu’un signe
$l_{-}^{\prime \prime }$
sont de dimension impaire, on voit qu’un signe
![]() $-$
se glisse dans le produit des déterminants normalisés. C’est-à-dire que
$-$
se glisse dans le produit des déterminants normalisés. C’est-à-dire que
![]() $\unicode[STIX]{x1D702}^{\prime \prime }=-\unicode[STIX]{x1D702}_{+}^{\prime \prime }\unicode[STIX]{x1D702}_{-}^{\prime \prime }\prod _{i\in I}\unicode[STIX]{x1D702}_{i}^{\prime \prime }$
. D’où
$\unicode[STIX]{x1D702}^{\prime \prime }=-\unicode[STIX]{x1D702}_{+}^{\prime \prime }\unicode[STIX]{x1D702}_{-}^{\prime \prime }\prod _{i\in I}\unicode[STIX]{x1D702}_{i}^{\prime \prime }$
. D’où
La somme
![]() $\operatorname{val}_{F}(\unicode[STIX]{x1D702}_{+})+\operatorname{val}_{F}(\unicode[STIX]{x1D702}_{-})$
est nulle d’après (2). Avec les formules ci-dessus, on obtient
$\operatorname{val}_{F}(\unicode[STIX]{x1D702}_{+})+\operatorname{val}_{F}(\unicode[STIX]{x1D702}_{-})$
est nulle d’après (2). Avec les formules ci-dessus, on obtient
Mais
![]() $\operatorname{sgn}(\unicode[STIX]{x1D702}_{+}\unicode[STIX]{x1D702}_{-})=(-1)^{d}$
d’après (2). D’où encore l’égalité (3) puisque
$\operatorname{sgn}(\unicode[STIX]{x1D702}_{+}\unicode[STIX]{x1D702}_{-})=(-1)^{d}$
d’après (2). D’où encore l’égalité (3) puisque
![]() $\operatorname{val}_{F}(\unicode[STIX]{x1D702}_{-})$
est impaire.◻
$\operatorname{val}_{F}(\unicode[STIX]{x1D702}_{-})$
est impaire.◻
Soit
![]() $(n_{1},n_{2})\in D(n)$
, auquel est associée une donnée endoscopique de
$(n_{1},n_{2})\in D(n)$
, auquel est associée une donnée endoscopique de
![]() $G_{\operatorname{iso}}$
et
$G_{\operatorname{iso}}$
et
![]() $G_{\operatorname{an}}$
, dont le groupe endoscopique est
$G_{\operatorname{an}}$
, dont le groupe endoscopique est
![]() $G_{n_{1},\operatorname{iso}}\times G_{n_{2},\operatorname{iso}}$
. Soit
$G_{n_{1},\operatorname{iso}}\times G_{n_{2},\operatorname{iso}}$
. Soit
![]() $(x_{1},x_{2})\in G_{n_{1},\operatorname{iso}}(F)\times G_{n_{2},\operatorname{iso}}(F)$
un couple
$(x_{1},x_{2})\in G_{n_{1},\operatorname{iso}}(F)\times G_{n_{2},\operatorname{iso}}(F)$
un couple
![]() $n$
-régulier formé d’éléments elliptiques. Pour
$n$
-régulier formé d’éléments elliptiques. Pour
![]() $\sharp =\operatorname{iso}$
ou
$\sharp =\operatorname{iso}$
ou
![]() $\operatorname{an}$
, soit
$\operatorname{an}$
, soit
![]() $x\in G_{\sharp }(F)$
un élément de la classe totale de conjugaison stable correspondant à
$x\in G_{\sharp }(F)$
un élément de la classe totale de conjugaison stable correspondant à
![]() $(x_{1},x_{2})$
. On lui associe les données
$(x_{1},x_{2})$
. On lui associe les données
![]() $\unicode[STIX]{x1D702}_{+}$
,
$\unicode[STIX]{x1D702}_{+}$
,
![]() $n_{+}$
,
$n_{+}$
,
![]() $\unicode[STIX]{x1D702}_{-}$
, etc., comme ci-dessus. Pour
$\unicode[STIX]{x1D702}_{-}$
, etc., comme ci-dessus. Pour
![]() $j=1,2$
, on pose
$j=1,2$
, on pose
![]() $x_{j}=s_{j}E(\text{}\underline{X}_{j})$
. On adopte la notation
$x_{j}=s_{j}E(\text{}\underline{X}_{j})$
. On adopte la notation
![]() $\text{}\underline{X}_{j}$
plutôt que
$\text{}\underline{X}_{j}$
plutôt que
![]() $X_{j}$
pour une raison qui apparaîtra plus loin. On définit de même les données
$X_{j}$
pour une raison qui apparaîtra plus loin. On définit de même les données
![]() $\unicode[STIX]{x1D702}_{j,+}$
,
$\unicode[STIX]{x1D702}_{j,+}$
,
![]() $n_{j,+}$
,
$n_{j,+}$
,
![]() $\unicode[STIX]{x1D702}_{j,-}$
, etc. On vérifie que
$\unicode[STIX]{x1D702}_{j,-}$
, etc. On vérifie que
![]() $n_{+}=n_{1,+}+n_{2,+}$
,
$n_{+}=n_{1,+}+n_{2,+}$
,
![]() $\unicode[STIX]{x1D702}_{+}=\unicode[STIX]{x1D702}_{1,+}\unicode[STIX]{x1D702}_{2,+}$
,
$\unicode[STIX]{x1D702}_{+}=\unicode[STIX]{x1D702}_{1,+}\unicode[STIX]{x1D702}_{2,+}$
,
![]() $n_{-}=n_{1,-}+n_{2,-}$
,
$n_{-}=n_{1,-}+n_{2,-}$
,
![]() $\unicode[STIX]{x1D702}_{-}=\unicode[STIX]{x1D702}_{1,-}\unicode[STIX]{x1D702}_{2,-}$
, que
$\unicode[STIX]{x1D702}_{-}=\unicode[STIX]{x1D702}_{1,-}\unicode[STIX]{x1D702}_{2,-}$
, que
![]() $I=I_{1}\cup I_{2}$
et que, pour
$I=I_{1}\cup I_{2}$
et que, pour
![]() $i\in I$
,
$i\in I$
,
![]() $d_{i}=d_{1,i}+d_{2,i}$
(avec
$d_{i}=d_{1,i}+d_{2,i}$
(avec
![]() $d_{j,i}=0$
si
$d_{j,i}=0$
si
![]() $i\not \in I_{j}$
). Le couple
$i\not \in I_{j}$
). Le couple
![]() $(n_{1,+},n_{2,+})$
, respectivement le quadruplet
$(n_{1,+},n_{2,+})$
, respectivement le quadruplet
![]() $(n_{1,-},\unicode[STIX]{x1D702}_{1,-},n_{2,-},\unicode[STIX]{x1D702}_{2,-})$
, respectivement le couple
$(n_{1,-},\unicode[STIX]{x1D702}_{1,-},n_{2,-},\unicode[STIX]{x1D702}_{2,-})$
, respectivement le couple
![]() $(d_{1,i},d_{2,i})$
pour
$(d_{1,i},d_{2,i})$
pour
![]() $i\in I$
, définit une donnée endoscopique de
$i\in I$
, définit une donnée endoscopique de
![]() $G_{+}$
, respectivement
$G_{+}$
, respectivement
![]() $G_{-}$
,
$G_{-}$
,
![]() $G_{i}$
. Avec les définitions que l’on a données, le couple
$G_{i}$
. Avec les définitions que l’on a données, le couple
![]() $(\text{}\underline{X}_{1,+},\text{}\underline{X}_{2,+})$
(par exemple) n’a pas de raison d’appartenir au groupe endoscopique associé à
$(\text{}\underline{X}_{1,+},\text{}\underline{X}_{2,+})$
(par exemple) n’a pas de raison d’appartenir au groupe endoscopique associé à
![]() $(n_{1,+},n_{2,+})$
car ce dernier est
$(n_{1,+},n_{2,+})$
car ce dernier est
![]() $G_{n_{1,+},\operatorname{iso}}\times G_{n_{2,+},\operatorname{iso}}$
tandis que
$G_{n_{1,+},\operatorname{iso}}\times G_{n_{2,+},\operatorname{iso}}$
tandis que
![]() $(\text{}\underline{X}_{1,+},\text{}\underline{X}_{2,+})$
appartient à un certain produit
$(\text{}\underline{X}_{1,+},\text{}\underline{X}_{2,+})$
appartient à un certain produit
![]() $G_{n_{1,+},\sharp _{1,+}}(F)\times G_{n_{2,+},\sharp _{2,+}}(F)$
. Mais seule la classe totale de conjugaison stable de
$G_{n_{1,+},\sharp _{1,+}}(F)\times G_{n_{2,+},\sharp _{2,+}}(F)$
. Mais seule la classe totale de conjugaison stable de
![]() $(\text{}\underline{X}_{1,+},\text{}\underline{X}_{2,+})$
interviendra dans la suite et on peut fixer un élément
$(\text{}\underline{X}_{1,+},\text{}\underline{X}_{2,+})$
interviendra dans la suite et on peut fixer un élément
![]() $(X_{1,+},X_{2,+})$
de cette classe qui appartient à
$(X_{1,+},X_{2,+})$
de cette classe qui appartient à
![]() $G_{n_{1,+},\operatorname{iso}}(F)\times G_{n_{2,+},\operatorname{iso}}(F)$
. On définit de même
$G_{n_{1,+},\operatorname{iso}}(F)\times G_{n_{2,+},\operatorname{iso}}(F)$
. On définit de même
![]() $(X_{1,-},X_{2,-})$
et
$(X_{1,-},X_{2,-})$
et
![]() $(X_{1,i},X_{2,i})$
pour
$(X_{1,i},X_{2,i})$
pour
![]() $i\in I$
. On pose
$i\in I$
. On pose
![]() $X_{1}=X_{1,+}\oplus {X_{1,-}\oplus \oplus }_{i\in I}X_{1,i}$
et on définit de même
$X_{1}=X_{1,+}\oplus {X_{1,-}\oplus \oplus }_{i\in I}X_{1,i}$
et on définit de même
![]() $X_{2}$
.
$X_{2}$
.
On dispose d’un facteur de transfert
![]() $\unicode[STIX]{x1D6E5}((x_{1},x_{2}),x)$
associé à la donnée endoscopique définie par
$\unicode[STIX]{x1D6E5}((x_{1},x_{2}),x)$
associé à la donnée endoscopique définie par
![]() $(n_{1},n_{2})$
. On dispose d’un facteur de transfert, que nous noterons simplement
$(n_{1},n_{2})$
. On dispose d’un facteur de transfert, que nous noterons simplement
![]() $\unicode[STIX]{x1D6E5}_{+}((X_{1,+},X_{2,+}),X_{+})$
, associé à la donnée endoscopique définie par
$\unicode[STIX]{x1D6E5}_{+}((X_{1,+},X_{2,+}),X_{+})$
, associé à la donnée endoscopique définie par
![]() $(n_{1,+},n_{2,+})$
et, de même, de facteurs de transfert
$(n_{1,+},n_{2,+})$
et, de même, de facteurs de transfert
![]() $\unicode[STIX]{x1D6E5}_{-}((X_{1,-},X_{2,-}),X_{-})$
et
$\unicode[STIX]{x1D6E5}_{-}((X_{1,-},X_{2,-}),X_{-})$
et
![]() $\unicode[STIX]{x1D6E5}_{i}((X_{1,i},X_{2,i}),X_{i})$
. Ces trois derniers facteurs sont normalisés comme dans les paragraphes 2.1, 2.2 et 2.3. On pose
$\unicode[STIX]{x1D6E5}_{i}((X_{1,i},X_{2,i}),X_{i})$
. Ces trois derniers facteurs sont normalisés comme dans les paragraphes 2.1, 2.2 et 2.3. On pose
 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6E5}((X_{1},X_{2}),X) & = & \displaystyle \unicode[STIX]{x1D6E5}_{+}((X_{1,+},X_{2,+}),X_{+})\unicode[STIX]{x1D6E5}_{-}((X_{1,-},X_{2,-}),X_{-})\nonumber\\ \displaystyle & & \displaystyle \times \,\displaystyle \mathop{\prod }_{i\in I}\unicode[STIX]{x1D6E5}_{i}((X_{1,i},X_{2,i}),X_{i})\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6E5}((X_{1},X_{2}),X) & = & \displaystyle \unicode[STIX]{x1D6E5}_{+}((X_{1,+},X_{2,+}),X_{+})\unicode[STIX]{x1D6E5}_{-}((X_{1,-},X_{2,-}),X_{-})\nonumber\\ \displaystyle & & \displaystyle \times \,\displaystyle \mathop{\prod }_{i\in I}\unicode[STIX]{x1D6E5}_{i}((X_{1,i},X_{2,i}),X_{i})\nonumber\end{eqnarray}$$
et
Lemme. On a l’égalité
Preuve.
Notons
![]() $K_{+}$
l’ensemble des orbites de l’action de
$K_{+}$
l’ensemble des orbites de l’action de
![]() $\operatorname{Gal}(\bar{F}/F)$
dans l’ensemble des valeurs propres de
$\operatorname{Gal}(\bar{F}/F)$
dans l’ensemble des valeurs propres de
![]() $X_{+}$
différentes de
$X_{+}$
différentes de
![]() $0$
(la valeur propre
$0$
(la valeur propre
![]() $0$
intervient avec multiplicité
$0$
intervient avec multiplicité
![]() $1$
),
$1$
),
![]() $K_{-}$
l’ensemble des orbites de l’action de
$K_{-}$
l’ensemble des orbites de l’action de
![]() $\operatorname{Gal}(\bar{F}/F)$
dans l’ensemble des valeurs propres de
$\operatorname{Gal}(\bar{F}/F)$
dans l’ensemble des valeurs propres de
![]() $X_{-}$
et, pour
$X_{-}$
et, pour
![]() $i\in I$
,
$i\in I$
,
![]() $K_{i}$
l’ensemble des orbites de l’action de
$K_{i}$
l’ensemble des orbites de l’action de
![]() $\operatorname{Gal}(\bar{F}/E_{i})$
dans l’ensemble des valeurs propres de
$\operatorname{Gal}(\bar{F}/E_{i})$
dans l’ensemble des valeurs propres de
![]() $X_{i}$
, vu comme un endomorphisme
$X_{i}$
, vu comme un endomorphisme
![]() $E_{i}$
-linéaire de
$E_{i}$
-linéaire de
![]() $V_{i}$
. Pour
$V_{i}$
. Pour
![]() $k\in K_{+}$
, respectivement
$k\in K_{+}$
, respectivement
![]() $k\in K_{-}$
,
$k\in K_{-}$
,
![]() $k\in K_{i}$
, on fixe
$k\in K_{i}$
, on fixe
![]() $\unicode[STIX]{x1D6EF}_{k}\in k$
. On pose
$\unicode[STIX]{x1D6EF}_{k}\in k$
. On pose
![]() $E(\unicode[STIX]{x1D6EF}_{k})=(1+\unicode[STIX]{x1D6EF}_{k}/2)(1-\unicode[STIX]{x1D6EF}_{k}/2)^{-1}$
. Pour
$E(\unicode[STIX]{x1D6EF}_{k})=(1+\unicode[STIX]{x1D6EF}_{k}/2)(1-\unicode[STIX]{x1D6EF}_{k}/2)^{-1}$
. Pour
![]() $k\in K_{+}\cup K_{-}$
, on pose
$k\in K_{+}\cup K_{-}$
, on pose
![]() $F_{k}=F[\unicode[STIX]{x1D6EF}_{k}]$
. Il existe une sous-extension
$F_{k}=F[\unicode[STIX]{x1D6EF}_{k}]$
. Il existe une sous-extension
![]() $F_{k}^{\natural }$
de
$F_{k}^{\natural }$
de
![]() $F$
telle que
$F$
telle que
![]() $[F_{k}:F_{k}^{\natural }]=2$
et que
$[F_{k}:F_{k}^{\natural }]=2$
et que
![]() $\operatorname{trace}_{F_{k}/F_{k}^{\natural }}(\unicode[STIX]{x1D6EF}_{k})=0$
. Pour
$\operatorname{trace}_{F_{k}/F_{k}^{\natural }}(\unicode[STIX]{x1D6EF}_{k})=0$
. Pour
![]() $i\in I$
et
$i\in I$
et
![]() $k\in K_{i}$
, on pose
$k\in K_{i}$
, on pose
![]() $F_{k}=E_{i}[\unicode[STIX]{x1D6EF}_{k}]$
. Il existe une extension
$F_{k}=E_{i}[\unicode[STIX]{x1D6EF}_{k}]$
. Il existe une extension
![]() $F_{k}^{\natural }$
de
$F_{k}^{\natural }$
de
![]() $E_{i}^{\natural }$
de sorte que
$E_{i}^{\natural }$
de sorte que
![]() $F_{k}$
soit le composé des extensions
$F_{k}$
soit le composé des extensions
![]() $E_{i}$
et
$E_{i}$
et
![]() $F_{k}^{\natural }$
de
$F_{k}^{\natural }$
de
![]() $E_{i}^{\natural }$
, et que
$E_{i}^{\natural }$
, et que
![]() $\operatorname{trace}_{F_{k}/F_{k}^{\natural }}(\unicode[STIX]{x1D6EF}_{k})=0$
. On note
$\operatorname{trace}_{F_{k}/F_{k}^{\natural }}(\unicode[STIX]{x1D6EF}_{k})=0$
. On note
![]() $K$
l’union disjointe de
$K$
l’union disjointe de
![]() $K_{+}$
,
$K_{+}$
,
![]() $K_{-}$
et des
$K_{-}$
et des
![]() $K_{i}$
pour
$K_{i}$
pour
![]() $i\in I$
. L’ensemble des valeurs propres de
$i\in I$
. L’ensemble des valeurs propres de
![]() $x$
différentes de
$x$
différentes de
![]() $1$
est l’ensemble des conjugués par
$1$
est l’ensemble des conjugués par
![]() $\operatorname{Gal}(\bar{F}/F)$
des éléments
$\operatorname{Gal}(\bar{F}/F)$
des éléments
![]() $\unicode[STIX]{x1D709}_{k}=E(\unicode[STIX]{x1D6EF}_{k})$
pour
$\unicode[STIX]{x1D709}_{k}=E(\unicode[STIX]{x1D6EF}_{k})$
pour
![]() $k\in K_{+}$
;
$k\in K_{+}$
;
![]() $\unicode[STIX]{x1D709}_{k}=-E(\unicode[STIX]{x1D6EF}_{k})$
pour
$\unicode[STIX]{x1D709}_{k}=-E(\unicode[STIX]{x1D6EF}_{k})$
pour
![]() $k\in K_{-}$
;
$k\in K_{-}$
;
![]() $\unicode[STIX]{x1D709}_{k}=s_{i}E(\unicode[STIX]{x1D6EF}_{k})$
pour
$\unicode[STIX]{x1D709}_{k}=s_{i}E(\unicode[STIX]{x1D6EF}_{k})$
pour
![]() $i\in I$
et
$i\in I$
et
![]() $k\in K_{i}$
.
$k\in K_{i}$
.
Pour
![]() $k\in K$
, notons
$k\in K$
, notons
![]() $V_{k}$
la somme des espaces propres de
$V_{k}$
la somme des espaces propres de
![]() $x$
associés à des conjugués de
$x$
associés à des conjugués de
![]() $\unicode[STIX]{x1D709}_{k}$
. On peut identifier
$\unicode[STIX]{x1D709}_{k}$
. On peut identifier
![]() $V_{k}$
à
$V_{k}$
à
![]() $F_{k}$
de sorte que l’action de
$F_{k}$
de sorte que l’action de
![]() $x$
dans
$x$
dans
![]() $V_{k}$
s’identifie à la multiplication par
$V_{k}$
s’identifie à la multiplication par
![]() $\unicode[STIX]{x1D709}_{k}$
. Il existe un élément
$\unicode[STIX]{x1D709}_{k}$
. Il existe un élément
![]() $c_{k}\in F_{k}^{\natural }$
de sorte que la restriction de
$c_{k}\in F_{k}^{\natural }$
de sorte que la restriction de
![]() $Q_{\sharp }$
à
$Q_{\sharp }$
à
![]() $V_{k}$
s’identifie à la forme quadratique
$V_{k}$
s’identifie à la forme quadratique
sur
![]() $F_{k}$
, où
$F_{k}$
, où
![]() $\unicode[STIX]{x1D70F}_{k}$
est l’élément non trivial de
$\unicode[STIX]{x1D70F}_{k}$
est l’élément non trivial de
![]() $\operatorname{Gal}(F_{k}/F_{k}^{\natural })$
. Seule compte la classe de
$\operatorname{Gal}(F_{k}/F_{k}^{\natural })$
. Seule compte la classe de
![]() $c_{k}$
modulo les normes de l’extension
$c_{k}$
modulo les normes de l’extension
![]() $F_{k}/F_{k}^{\natural }$
. On note
$F_{k}/F_{k}^{\natural }$
. On note
![]() $\operatorname{sgn}_{k}$
le caractère quadratique de
$\operatorname{sgn}_{k}$
le caractère quadratique de
![]() $F_{k}^{\natural ,\times }$
associé à cette extension. On note
$F_{k}^{\natural ,\times }$
associé à cette extension. On note
![]() $P_{k}$
le polynôme caractéristique de
$P_{k}$
le polynôme caractéristique de
![]() $\unicode[STIX]{x1D709}_{k}$
sur
$\unicode[STIX]{x1D709}_{k}$
sur
![]() $F$
. On note
$F$
. On note
![]() $P$
le produit de ces polynômes. Pour tout polynôme
$P$
le produit de ces polynômes. Pour tout polynôme
![]() $R$
, on note
$R$
, on note
![]() $R^{\prime }$
son polynôme dérivé. On pose
$R^{\prime }$
son polynôme dérivé. On pose
On définit
![]() $K_{1}$
et
$K_{1}$
et
![]() $K_{2}$
comme on a défini
$K_{2}$
comme on a défini
![]() $K$
. L’ensemble
$K$
. L’ensemble
![]() $K$
est l’union disjointe de
$K$
est l’union disjointe de
![]() $K_{1}$
et
$K_{1}$
et
![]() $K_{2}$
. L’union est disjointe car
$K_{2}$
. L’union est disjointe car
![]() $(x_{1},x_{2})$
est
$(x_{1},x_{2})$
est
![]() $n$
-régulier. D’après [Reference Waldspurger7] proposition 1.10, on a l’égalité
$n$
-régulier. D’après [Reference Waldspurger7] proposition 1.10, on a l’égalité
Remarque.
Dans la formule de [Reference Waldspurger7] définissant
![]() $C_{k}$
, il n’y a pas le facteur
$C_{k}$
, il n’y a pas le facteur
![]() $[F_{k}:F]$
. Mais le terme
$[F_{k}:F]$
. Mais le terme
![]() $c_{k}$
y est défini différemment : c’est notre
$c_{k}$
y est défini différemment : c’est notre
![]() $c_{k}$
multiplié par
$c_{k}$
multiplié par
![]() $[F_{k}:F]^{-1}$
.
$[F_{k}:F]^{-1}$
.
Pour
![]() $k\in K_{+}\cup K_{-}$
, on note
$k\in K_{+}\cup K_{-}$
, on note
![]() $\mathfrak{P}_{k}$
le polynôme caractéristique de
$\mathfrak{P}_{k}$
le polynôme caractéristique de
![]() $\unicode[STIX]{x1D6EF}_{k}$
sur
$\unicode[STIX]{x1D6EF}_{k}$
sur
![]() $F$
. On pose
$F$
. On pose
![]() $\mathfrak{C}_{k}=(-1)^{n_{+}}\unicode[STIX]{x1D702}_{+}[F_{k}:F]c_{k}\unicode[STIX]{x1D6EF}_{k}\mathfrak{P}_{k}^{\prime }(\unicode[STIX]{x1D6EF}_{k})\prod _{k^{\prime }\in K_{+},k^{\prime }\not =k}\mathfrak{P}_{k^{\prime }}(\unicode[STIX]{x1D6EF}_{k})$
, si
$\mathfrak{C}_{k}=(-1)^{n_{+}}\unicode[STIX]{x1D702}_{+}[F_{k}:F]c_{k}\unicode[STIX]{x1D6EF}_{k}\mathfrak{P}_{k}^{\prime }(\unicode[STIX]{x1D6EF}_{k})\prod _{k^{\prime }\in K_{+},k^{\prime }\not =k}\mathfrak{P}_{k^{\prime }}(\unicode[STIX]{x1D6EF}_{k})$
, si
![]() $k\in K_{+}$
;
$k\in K_{+}$
;
![]() $\mathfrak{C}_{k}=(-1)^{n_{-}}\unicode[STIX]{x1D702}_{-}[F_{k}:F]c_{k}\unicode[STIX]{x1D6EF}_{k}^{-1}\mathfrak{P}_{k}^{\prime }(\unicode[STIX]{x1D6EF}_{k})\prod _{k^{\prime }\in K_{-},k^{\prime }\not =k}\mathfrak{P}_{k^{\prime }}(\unicode[STIX]{x1D6EF}_{k})$
, si
$\mathfrak{C}_{k}=(-1)^{n_{-}}\unicode[STIX]{x1D702}_{-}[F_{k}:F]c_{k}\unicode[STIX]{x1D6EF}_{k}^{-1}\mathfrak{P}_{k}^{\prime }(\unicode[STIX]{x1D6EF}_{k})\prod _{k^{\prime }\in K_{-},k^{\prime }\not =k}\mathfrak{P}_{k^{\prime }}(\unicode[STIX]{x1D6EF}_{k})$
, si
![]() $k\in K_{-}$
.
$k\in K_{-}$
.
Pour
![]() $i\in I$
et
$i\in I$
et
![]() $k\in K_{i}$
, on note
$k\in K_{i}$
, on note
![]() $\mathfrak{P}_{i,k}$
le polynôme caractéristique de
$\mathfrak{P}_{i,k}$
le polynôme caractéristique de
![]() $\unicode[STIX]{x1D6EF}_{k}$
sur
$\unicode[STIX]{x1D6EF}_{k}$
sur
![]() $E_{i}$
. On fixe un élément
$E_{i}$
. On fixe un élément
![]() $\unicode[STIX]{x1D702}_{i}\in E_{i}$
qui est une unité et vérifie
$\unicode[STIX]{x1D702}_{i}\in E_{i}$
qui est une unité et vérifie
![]() $\unicode[STIX]{x1D70F}_{i}(\unicode[STIX]{x1D702}_{i})=(-1)^{d_{i}+1}\unicode[STIX]{x1D702}_{i}$
, où
$\unicode[STIX]{x1D70F}_{i}(\unicode[STIX]{x1D702}_{i})=(-1)^{d_{i}+1}\unicode[STIX]{x1D702}_{i}$
, où
![]() $\unicode[STIX]{x1D70F}_{i}$
est l’unique élément non trivial de
$\unicode[STIX]{x1D70F}_{i}$
est l’unique élément non trivial de
![]() $\operatorname{Gal}(E_{i}/E_{i}^{\natural })$
. On pose
$\operatorname{Gal}(E_{i}/E_{i}^{\natural })$
. On pose
![]() $\mathfrak{C}_{k}=\unicode[STIX]{x1D702}_{i}[F_{k}:E_{i}]c_{k}\mathfrak{P}_{i,k}^{\prime }(\unicode[STIX]{x1D6EF}_{k})\prod _{k^{\prime }\in K_{i},k^{\prime }\not =k}\mathfrak{P}_{i,k^{\prime }}(\unicode[STIX]{x1D6EF}_{k})$
.
$\mathfrak{C}_{k}=\unicode[STIX]{x1D702}_{i}[F_{k}:E_{i}]c_{k}\mathfrak{P}_{i,k}^{\prime }(\unicode[STIX]{x1D6EF}_{k})\prod _{k^{\prime }\in K_{i},k^{\prime }\not =k}\mathfrak{P}_{i,k^{\prime }}(\unicode[STIX]{x1D6EF}_{k})$
.
D’après [Reference Waldspurger9] lemme X.7, on a l’égalité
On va démontrer les propriétés suivantes :
(6) pour
![]() $k\in K_{+}\cup K_{-}$
,
$k\in K_{+}\cup K_{-}$
,
![]() $\operatorname{sgn}_{k}(C_{k})=\operatorname{sgn}_{k}(\mathfrak{C}_{k})$
;
$\operatorname{sgn}_{k}(C_{k})=\operatorname{sgn}_{k}(\mathfrak{C}_{k})$
;
(7) pour
![]() $i\in I$
et
$i\in I$
et
![]() $k\in K_{i}$
,
$k\in K_{i}$
,
![]() $\operatorname{sgn}_{k}(C_{k})=(-1)^{[F_{k}:E_{i}]\operatorname{val}_{F}(\unicode[STIX]{x1D702}_{-})}\operatorname{sgn}_{k}(\mathfrak{C}_{k})$
.
$\operatorname{sgn}_{k}(C_{k})=(-1)^{[F_{k}:E_{i}]\operatorname{val}_{F}(\unicode[STIX]{x1D702}_{-})}\operatorname{sgn}_{k}(\mathfrak{C}_{k})$
.
En les admettant, on voit que le rapport entre les membres de droite de (4) et (5) est
![]() $(-1)^{D\,\operatorname{val}_{F}(\unicode[STIX]{x1D702}_{-})}$
, où
$(-1)^{D\,\operatorname{val}_{F}(\unicode[STIX]{x1D702}_{-})}$
, où
![]() $D=\sum _{i\in I}\sum _{k\in K_{i}\cap K_{2}}[F_{k}:E_{i}]$
. La somme intérieure en
$D=\sum _{i\in I}\sum _{k\in K_{i}\cap K_{2}}[F_{k}:E_{i}]$
. La somme intérieure en
![]() $k$
vaut
$k$
vaut
![]() $d_{2,i}$
, donc
$d_{2,i}$
, donc
![]() $D=d_{2}$
. Alors les égalités (4) et (5) impliquent celle de l’énoncé.
$D=d_{2}$
. Alors les égalités (4) et (5) impliquent celle de l’énoncé.
Pour démontrer (6) et (7), on a besoin de quelques ingrédients. Soit
![]() $Z\in \bar{F}$
et
$Z\in \bar{F}$
et
![]() $\left(\!\begin{smallmatrix}a & b\\ c & d\end{smallmatrix}\!\right)\in \operatorname{GL}(2;F)$
. Supposons que
$\left(\!\begin{smallmatrix}a & b\\ c & d\end{smallmatrix}\!\right)\in \operatorname{GL}(2;F)$
. Supposons que
![]() $cZ+d\not =0$
et posons
$cZ+d\not =0$
et posons
![]() $z=\frac{az+b}{cz+d}$
. Notons
$z=\frac{az+b}{cz+d}$
. Notons
![]() $P_{z}(T)$
et
$P_{z}(T)$
et
![]() $P_{Z}(T)$
les polynômes caractéristiques de
$P_{Z}(T)$
les polynômes caractéristiques de
![]() $z$
et
$z$
et
![]() $Z$
, et notons
$Z$
, et notons
![]() $m$
leur degré. Alors on a les égalités
$m$
leur degré. Alors on a les égalités
Cf. [Reference Li3] lemme 7.4.1. D’autre part, pour
![]() $k\in K$
, on calcule facilement le déterminant non normalisé
$k\in K$
, on calcule facilement le déterminant non normalisé
![]() $\operatorname{det}_{k}\in F^{\times }/F^{\times 2}$
de la forme quadratique définie plus haut sur
$\operatorname{det}_{k}\in F^{\times }/F^{\times 2}$
de la forme quadratique définie plus haut sur
![]() $V_{k}$
: on a
$V_{k}$
: on a
Fixons une extension galoisienne finie
![]() $F^{\prime }$
de
$F^{\prime }$
de
![]() $F$
contenant tous les corps
$F$
contenant tous les corps
![]() $F_{k}$
. Notons
$F_{k}$
. Notons
![]() $\mathfrak{o}_{1}^{\prime }$
le groupe multiplicatif des unités de
$\mathfrak{o}_{1}^{\prime }$
le groupe multiplicatif des unités de
![]() $F^{\prime }$
congrues à
$F^{\prime }$
congrues à
![]() $1$
modulo l’idéal maximal
$1$
modulo l’idéal maximal
![]() $\mathfrak{p}^{\prime }$
de l’anneau des entiers de
$\mathfrak{p}^{\prime }$
de l’anneau des entiers de
![]() $F^{\prime }$
. Pour
$F^{\prime }$
. Pour
![]() $k\in K_{+}\cup K_{-}$
, introduisons la relation d’équivalence dans
$k\in K_{+}\cup K_{-}$
, introduisons la relation d’équivalence dans
![]() $F^{^{\prime }\times }$
:
$F^{^{\prime }\times }$
:
![]() $x\equiv _{k}y$
si et seulement s’il existe
$x\equiv _{k}y$
si et seulement s’il existe
![]() $x^{\prime }\in \mathfrak{o}_{1}^{\prime }$
et
$x^{\prime }\in \mathfrak{o}_{1}^{\prime }$
et
![]() $y^{\prime }\in F_{k}^{\times }$
tels que
$y^{\prime }\in F_{k}^{\times }$
tels que
![]() $xy^{-1}=x^{\prime }\,\operatorname{norme}_{F_{k}/F_{k}^{\natural }}(y^{\prime })$
. On peut remplacer la relation (6) par
$xy^{-1}=x^{\prime }\,\operatorname{norme}_{F_{k}/F_{k}^{\natural }}(y^{\prime })$
. On peut remplacer la relation (6) par
(11) pour
![]() $k\in K_{+}\cup K_{-}$
,
$k\in K_{+}\cup K_{-}$
,
![]() $C_{k}\equiv _{k}\mathfrak{C}_{k}$
.
$C_{k}\equiv _{k}\mathfrak{C}_{k}$
.
En effet, si cette relation est vérifiée, il existe
![]() $x\in \mathfrak{o}_{1}^{\prime }$
et
$x\in \mathfrak{o}_{1}^{\prime }$
et
![]() $y\in F_{k}^{\times }$
tels que
$y\in F_{k}^{\times }$
tels que
![]() $C_{k}=x\,\operatorname{norme}_{F_{k}/F_{k}^{\natural }}(y)\mathfrak{C}_{k}$
. On sait que les termes
$C_{k}=x\,\operatorname{norme}_{F_{k}/F_{k}^{\natural }}(y)\mathfrak{C}_{k}$
. On sait que les termes
![]() $C_{k}$
et
$C_{k}$
et
![]() $\mathfrak{C}_{k}$
appartiennent à
$\mathfrak{C}_{k}$
appartiennent à
![]() $F_{k}^{\natural ,\times }$
. Donc
$F_{k}^{\natural ,\times }$
. Donc
![]() $x\in \mathfrak{o}_{1}^{\prime }\cap F_{k}^{\natural ,\times }$
. Parce que
$x\in \mathfrak{o}_{1}^{\prime }\cap F_{k}^{\natural ,\times }$
. Parce que
![]() $p$
est grand, le caractère
$p$
est grand, le caractère
![]() $\operatorname{sgn}_{k}$
est modérément ramifié, donc
$\operatorname{sgn}_{k}$
est modérément ramifié, donc
![]() $\operatorname{sgn}_{k}(x)=1$
. On a aussi
$\operatorname{sgn}_{k}(x)=1$
. On a aussi
![]() $\operatorname{sgn}_{k}(\operatorname{norme}_{F_{k}/F_{k}^{\natural }}(y))=1$
. L’égalité
$\operatorname{sgn}_{k}(\operatorname{norme}_{F_{k}/F_{k}^{\natural }}(y))=1$
. L’égalité
![]() $\operatorname{sgn}_{k}(C_{k})=\operatorname{sgn}_{k}(\mathfrak{C}_{k})$
s’ensuit.
$\operatorname{sgn}_{k}(C_{k})=\operatorname{sgn}_{k}(\mathfrak{C}_{k})$
s’ensuit.
Soit
![]() $k\in K_{+}$
. Pour
$k\in K_{+}$
. Pour
![]() $k^{\prime }\in K_{-}$
ou
$k^{\prime }\in K_{-}$
ou
![]() $k^{\prime }\in K_{i}$
pour
$k^{\prime }\in K_{i}$
pour
![]() $i\in I$
, la contribution de
$i\in I$
, la contribution de
![]() $k^{\prime }$
à
$k^{\prime }$
à
![]() $C_{k}$
est
$C_{k}$
est
![]() $P_{k^{\prime }}(\unicode[STIX]{x1D709}_{k})P_{k^{\prime }}(-1)$
. On a
$P_{k^{\prime }}(\unicode[STIX]{x1D709}_{k})P_{k^{\prime }}(-1)$
. On a
![]() $\unicode[STIX]{x1D709}_{k}\in \mathfrak{o}_{1}^{\prime }$
tandis que les racines de
$\unicode[STIX]{x1D709}_{k}\in \mathfrak{o}_{1}^{\prime }$
tandis que les racines de
![]() $P_{k^{\prime }}$
n’appartiennent pas à ce groupe. On en déduit
$P_{k^{\prime }}$
n’appartiennent pas à ce groupe. On en déduit
![]() $P_{k^{\prime }}(\unicode[STIX]{x1D709}_{k})\equiv _{k}P_{k^{\prime }}(1)\equiv _{k}P_{k^{\prime }}(1)^{-1}$
. Le produit
$P_{k^{\prime }}(\unicode[STIX]{x1D709}_{k})\equiv _{k}P_{k^{\prime }}(1)\equiv _{k}P_{k^{\prime }}(1)^{-1}$
. Le produit
![]() $P_{k^{\prime }}(1)^{-1}P_{k^{\prime }}(-1)$
est égal à
$P_{k^{\prime }}(1)^{-1}P_{k^{\prime }}(-1)$
est égal à
![]() $\operatorname{norme}_{F_{k^{\prime }}/F}(1-\unicode[STIX]{x1D709}_{k^{\prime }})^{-1}(-1-\unicode[STIX]{x1D709}_{k^{\prime }})$
. Parce que
$\operatorname{norme}_{F_{k^{\prime }}/F}(1-\unicode[STIX]{x1D709}_{k^{\prime }})^{-1}(-1-\unicode[STIX]{x1D709}_{k^{\prime }})$
. Parce que
![]() $\operatorname{norme}_{F_{k^{\prime }}/F_{k^{\prime }}^{\natural }}(\unicode[STIX]{x1D709}_{k^{\prime }})=1$
, on voit que
$\operatorname{norme}_{F_{k^{\prime }}/F_{k^{\prime }}^{\natural }}(\unicode[STIX]{x1D709}_{k^{\prime }})=1$
, on voit que
![]() $(1-\unicode[STIX]{x1D709}_{k^{\prime }})^{-1}(-1-\unicode[STIX]{x1D709}_{k^{\prime }})$
est un élément de
$(1-\unicode[STIX]{x1D709}_{k^{\prime }})^{-1}(-1-\unicode[STIX]{x1D709}_{k^{\prime }})$
est un élément de
![]() $F_{k^{\prime }}$
dont la trace dans
$F_{k^{\prime }}$
dont la trace dans
![]() $F_{k^{\prime }}^{\natural }$
est nulle. Il existe donc
$F_{k^{\prime }}^{\natural }$
est nulle. Il existe donc
![]() $x\in F_{k^{\prime }}^{\natural ,\times }$
tel que
$x\in F_{k^{\prime }}^{\natural ,\times }$
tel que
![]() $(1-\unicode[STIX]{x1D709}_{k^{\prime }})^{-1}(-1-\unicode[STIX]{x1D709}_{k^{\prime }})=x\unicode[STIX]{x1D6EF}_{k^{\prime }}$
. D’après (10), on a donc
$(1-\unicode[STIX]{x1D709}_{k^{\prime }})^{-1}(-1-\unicode[STIX]{x1D709}_{k^{\prime }})=x\unicode[STIX]{x1D6EF}_{k^{\prime }}$
. D’après (10), on a donc
Remarque.
Le terme
![]() $\operatorname{det}_{k^{\prime }}$
n’est défini que modulo
$\operatorname{det}_{k^{\prime }}$
n’est défini que modulo
![]() $F^{\times 2}$
. Supposons que l’on en choisisse un représentant dans
$F^{\times 2}$
. Supposons que l’on en choisisse un représentant dans
![]() $F^{\times }$
. La classe d’équivalence de ce représentant pour la relation
$F^{\times }$
. La classe d’équivalence de ce représentant pour la relation
![]() $\equiv _{k}$
est bien définie.
$\equiv _{k}$
est bien définie.
Soit
![]() $k^{\prime }\in K_{+}$
avec
$k^{\prime }\in K_{+}$
avec
![]() $k^{\prime }\not =k$
. La contribution de
$k^{\prime }\not =k$
. La contribution de
![]() $k^{\prime }$
à
$k^{\prime }$
à
![]() $C_{k}$
est
$C_{k}$
est
![]() $P_{k^{\prime }}(\unicode[STIX]{x1D709}_{k})P_{k^{\prime }}(-1)$
. On utilise (8) avec
$P_{k^{\prime }}(\unicode[STIX]{x1D709}_{k})P_{k^{\prime }}(-1)$
. On utilise (8) avec
![]() $\left(\!\begin{smallmatrix}a & b\\ c & d\end{smallmatrix}\!\right)=\left(\begin{smallmatrix}-\frac{1}{2} & 1\\ -\frac{1}{2} & 1\end{smallmatrix}\right)$
,
$\left(\!\begin{smallmatrix}a & b\\ c & d\end{smallmatrix}\!\right)=\left(\begin{smallmatrix}-\frac{1}{2} & 1\\ -\frac{1}{2} & 1\end{smallmatrix}\right)$
,
![]() $Z=\unicode[STIX]{x1D6EF}_{k^{\prime }}$
et
$Z=\unicode[STIX]{x1D6EF}_{k^{\prime }}$
et
![]() $T=\unicode[STIX]{x1D6EF}_{k}$
. L’entier
$T=\unicode[STIX]{x1D6EF}_{k}$
. L’entier
![]() $m=[F_{k^{\prime }}:F]$
est pair. De plus,
$m=[F_{k^{\prime }}:F]$
est pair. De plus,
![]() $\unicode[STIX]{x1D6EF}_{k}\in \mathfrak{p}^{\prime }$
, donc
$\unicode[STIX]{x1D6EF}_{k}\in \mathfrak{p}^{\prime }$
, donc
![]() $c\unicode[STIX]{x1D6EF}_{k}+d\in \mathfrak{o}_{1}^{\prime }$
. On obtient
$c\unicode[STIX]{x1D6EF}_{k}+d\in \mathfrak{o}_{1}^{\prime }$
. On obtient
![]() $P_{k^{\prime }}(\unicode[STIX]{x1D709}_{k})\equiv _{k}P_{k^{\prime }}(-1)\mathfrak{P}_{k^{\prime }}(\unicode[STIX]{x1D6EF}_{k})$
. D’où
$P_{k^{\prime }}(\unicode[STIX]{x1D709}_{k})\equiv _{k}P_{k^{\prime }}(-1)\mathfrak{P}_{k^{\prime }}(\unicode[STIX]{x1D6EF}_{k})$
. D’où
Un calcul analogue s’applique au terme
![]() $P_{k}^{\prime }(\unicode[STIX]{x1D709}_{k})P_{k}(-1)$
, en utilisant cette fois la relation (9). On obtient
$P_{k}^{\prime }(\unicode[STIX]{x1D709}_{k})P_{k}(-1)$
, en utilisant cette fois la relation (9). On obtient
Évidemment,
![]() $\unicode[STIX]{x1D709}_{k}^{1-n}\equiv _{k}1$
et
$\unicode[STIX]{x1D709}_{k}^{1-n}\equiv _{k}1$
et
![]() $1+\unicode[STIX]{x1D709}_{k}\equiv _{k}2$
. On calcule
$1+\unicode[STIX]{x1D709}_{k}\equiv _{k}2$
. On calcule
 $$\begin{eqnarray}\displaystyle (\unicode[STIX]{x1D709}_{k}-1)^{-1} & = & \displaystyle (1-\unicode[STIX]{x1D6EF}_{k}/2)\unicode[STIX]{x1D6EF}_{k}^{-1}\equiv _{k}\unicode[STIX]{x1D6EF}_{k}^{-1}=-\unicode[STIX]{x1D6EF}_{k}(-\unicode[STIX]{x1D6EF}_{k}^{2})^{-1}\nonumber\\ \displaystyle & = & \displaystyle -\unicode[STIX]{x1D6EF}_{k}\operatorname{norme}_{F_{k}/F_{k}^{\natural }}(\unicode[STIX]{x1D6EF}_{k})^{-1}\equiv _{k}-\unicode[STIX]{x1D6EF}_{k}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle (\unicode[STIX]{x1D709}_{k}-1)^{-1} & = & \displaystyle (1-\unicode[STIX]{x1D6EF}_{k}/2)\unicode[STIX]{x1D6EF}_{k}^{-1}\equiv _{k}\unicode[STIX]{x1D6EF}_{k}^{-1}=-\unicode[STIX]{x1D6EF}_{k}(-\unicode[STIX]{x1D6EF}_{k}^{2})^{-1}\nonumber\\ \displaystyle & = & \displaystyle -\unicode[STIX]{x1D6EF}_{k}\operatorname{norme}_{F_{k}/F_{k}^{\natural }}(\unicode[STIX]{x1D6EF}_{k})^{-1}\equiv _{k}-\unicode[STIX]{x1D6EF}_{k}.\nonumber\end{eqnarray}$$
En rassemblant ces calculs, on obtient
où le produit porte sur les
![]() $k^{\prime }\in K_{-}$
et
$k^{\prime }\in K_{-}$
et
![]() $k^{\prime }\in K_{i}$
pour
$k^{\prime }\in K_{i}$
pour
![]() $i\in I$
. Le produit des
$i\in I$
. Le produit des
![]() $\operatorname{det}_{k^{\prime }}$
sur ces
$\operatorname{det}_{k^{\prime }}$
sur ces
![]() $k^{\prime }$
est le déterminant de la restriction de
$k^{\prime }$
est le déterminant de la restriction de
![]() $Q_{\sharp }$
à la somme de
$Q_{\sharp }$
à la somme de
![]() $V_{-}$
et des
$V_{-}$
et des
![]() $V_{i}$
pour
$V_{i}$
pour
![]() $i\in I$
. Il est égal au déterminant de
$i\in I$
. Il est égal au déterminant de
![]() $Q_{\sharp }$
divisé par le déterminant de la restriction de
$Q_{\sharp }$
divisé par le déterminant de la restriction de
![]() $Q_{\sharp }$
à
$Q_{\sharp }$
à
![]() $V_{+}$
. On a fixé le déterminant de
$V_{+}$
. On a fixé le déterminant de
![]() $Q_{\sharp }$
en [Reference Waldspurger11] 1.1 : c’est
$Q_{\sharp }$
en [Reference Waldspurger11] 1.1 : c’est
![]() $(-1)^{n}$
. Celui de la restriction de
$(-1)^{n}$
. Celui de la restriction de
![]() $Q_{\sharp }$
à
$Q_{\sharp }$
à
![]() $V_{+}$
est
$V_{+}$
est
![]() $(-1)^{n_{+}}\unicode[STIX]{x1D702}_{+}$
. L’équivalence ci-dessus entraîne alors (11).
$(-1)^{n_{+}}\unicode[STIX]{x1D702}_{+}$
. L’équivalence ci-dessus entraîne alors (11).
Soit
![]() $k\in K_{-}$
. Pour
$k\in K_{-}$
. Pour
![]() $k^{\prime }\in K_{+}$
ou
$k^{\prime }\in K_{+}$
ou
![]() $k^{\prime }\in K_{i}$
pour
$k^{\prime }\in K_{i}$
pour
![]() $i\in I$
, la contribution de
$i\in I$
, la contribution de
![]() $k^{\prime }$
à
$k^{\prime }$
à
![]() $C_{k}$
est
$C_{k}$
est
![]() $P_{k^{\prime }}(\unicode[STIX]{x1D709}_{k})P_{k^{\prime }}(-1)$
. On a
$P_{k^{\prime }}(\unicode[STIX]{x1D709}_{k})P_{k^{\prime }}(-1)$
. On a
![]() $\unicode[STIX]{x1D709}_{k}\in -\mathfrak{o}_{1}^{\prime }$
et les racines de
$\unicode[STIX]{x1D709}_{k}\in -\mathfrak{o}_{1}^{\prime }$
et les racines de
![]() $P_{k^{\prime }}$
ne sont pas congrues à
$P_{k^{\prime }}$
ne sont pas congrues à
![]() $-1$
modulo
$-1$
modulo
![]() $\mathfrak{p}^{\prime }$
. Donc
$\mathfrak{p}^{\prime }$
. Donc
![]() $P_{k^{\prime }}(\unicode[STIX]{x1D709}_{k})\equiv _{k}P_{k^{\prime }}(-1)$
, puis
$P_{k^{\prime }}(\unicode[STIX]{x1D709}_{k})\equiv _{k}P_{k^{\prime }}(-1)$
, puis
Pour
![]() $k^{\prime }\in K_{-}$
avec
$k^{\prime }\in K_{-}$
avec
![]() $k^{\prime }\not =k$
, la contribution de
$k^{\prime }\not =k$
, la contribution de
![]() $k^{\prime }$
à
$k^{\prime }$
à
![]() $C_{k}$
est
$C_{k}$
est
![]() $P_{k^{\prime }}(\unicode[STIX]{x1D709}_{k})P_{k^{\prime }}(-1)$
. On utilise (8) avec
$P_{k^{\prime }}(\unicode[STIX]{x1D709}_{k})P_{k^{\prime }}(-1)$
. On utilise (8) avec
![]() $\left(\!\begin{smallmatrix}a & b\\ c & d\end{smallmatrix}\!\right)=\left(\begin{smallmatrix}-\frac{1}{2} & -1\\ -\frac{1}{2} & 1\end{smallmatrix}\right)$
,
$\left(\!\begin{smallmatrix}a & b\\ c & d\end{smallmatrix}\!\right)=\left(\begin{smallmatrix}-\frac{1}{2} & -1\\ -\frac{1}{2} & 1\end{smallmatrix}\right)$
,
![]() $Z=\unicode[STIX]{x1D6EF}_{k^{\prime }}$
et
$Z=\unicode[STIX]{x1D6EF}_{k^{\prime }}$
et
![]() $T=\unicode[STIX]{x1D6EF}_{k}$
. De nouveau,
$T=\unicode[STIX]{x1D6EF}_{k}$
. De nouveau,
![]() $m$
est pair et
$m$
est pair et
![]() $c\unicode[STIX]{x1D6EF}_{k}+d\equiv _{k}1$
. D’où
$c\unicode[STIX]{x1D6EF}_{k}+d\equiv _{k}1$
. D’où
![]() $P_{k^{\prime }}(\unicode[STIX]{x1D709}_{k})\equiv _{k}P_{k^{\prime }}(1)\mathfrak{P}_{k^{\prime }}(\unicode[STIX]{x1D6EF}_{k})$
. Comme plus haut, on a
$P_{k^{\prime }}(\unicode[STIX]{x1D709}_{k})\equiv _{k}P_{k^{\prime }}(1)\mathfrak{P}_{k^{\prime }}(\unicode[STIX]{x1D6EF}_{k})$
. Comme plus haut, on a
D’où
Un même calcul s’applique au terme
![]() $P_{k}^{\prime }(\unicode[STIX]{x1D709}_{k})P_{k}(-1)$
, en utilisant cette fois la relation (9). Ici se glisse le déterminant
$P_{k}^{\prime }(\unicode[STIX]{x1D709}_{k})P_{k}(-1)$
, en utilisant cette fois la relation (9). Ici se glisse le déterminant
![]() $ad-bc$
qui vaut
$ad-bc$
qui vaut
![]() $-1$
. D’où
$-1$
. D’où
Évidemment,
![]() $\unicode[STIX]{x1D709}_{k}^{1-n}\equiv _{k}(-1)^{n-1}$
et
$\unicode[STIX]{x1D709}_{k}^{1-n}\equiv _{k}(-1)^{n-1}$
et
![]() $(\unicode[STIX]{x1D709}_{k}-1)^{-1}\equiv _{k}-2$
. On a
$(\unicode[STIX]{x1D709}_{k}-1)^{-1}\equiv _{k}-2$
. On a
En rassemblant ces calculs, on obtient
Le produit intervenant ici est le déterminant de la restriction de
![]() $Q_{\sharp }$
à
$Q_{\sharp }$
à
![]() $V_{-}$
, c’est-à-dire
$V_{-}$
, c’est-à-dire
![]() $(-1)^{n_{-}}\unicode[STIX]{x1D702}_{-}$
. D’où encore (11).
$(-1)^{n_{-}}\unicode[STIX]{x1D702}_{-}$
. D’où encore (11).
Soit
![]() $i\in I$
et
$i\in I$
et
![]() $k\in K_{i}$
. Cette fois, on définit dans
$k\in K_{i}$
. Cette fois, on définit dans
![]() $F^{^{\prime }\times }$
l’équivalence
$F^{^{\prime }\times }$
l’équivalence
![]() $x\equiv _{k}y$
si et seulement s’il existe
$x\equiv _{k}y$
si et seulement s’il existe
![]() $x^{\prime }\in F_{k}^{\times }$
tel que
$x^{\prime }\in F_{k}^{\times }$
tel que
![]() $xy^{-1}\operatorname{norme}_{F_{k}/F_{k}^{\natural }}(x^{\prime })$
soit une unité. Soit
$xy^{-1}\operatorname{norme}_{F_{k}/F_{k}^{\natural }}(x^{\prime })$
soit une unité. Soit
![]() $k^{\prime }\in K_{+}$
ou
$k^{\prime }\in K_{+}$
ou
![]() $k^{\prime }\in K_{i^{\prime }}$
pour un
$k^{\prime }\in K_{i^{\prime }}$
pour un
![]() $i^{\prime }\in I$
avec
$i^{\prime }\in I$
avec
![]() $i^{\prime }\not =i$
. Les racines du polynôme
$i^{\prime }\not =i$
. Les racines du polynôme
![]() $P_{k^{\prime }}$
ne sont congrues ni à
$P_{k^{\prime }}$
ne sont congrues ni à
![]() $-1$
, ni à
$-1$
, ni à
![]() $\unicode[STIX]{x1D709}_{k}$
modulo
$\unicode[STIX]{x1D709}_{k}$
modulo
![]() $\mathfrak{p}^{\prime }$
. On en déduit
$\mathfrak{p}^{\prime }$
. On en déduit
![]() $P_{k^{\prime }}(\unicode[STIX]{x1D709}_{k})P_{k^{\prime }}(-1)\equiv _{k}1$
. Soit
$P_{k^{\prime }}(\unicode[STIX]{x1D709}_{k})P_{k^{\prime }}(-1)\equiv _{k}1$
. Soit
![]() $k^{\prime }\in K_{-}$
. On a
$k^{\prime }\in K_{-}$
. On a
On a encore
![]() $P_{k^{\prime }}(\unicode[STIX]{x1D709}_{k})P_{k^{\prime }}(1)\equiv _{k}1$
et, par un calcul déjà effectué,
$P_{k^{\prime }}(\unicode[STIX]{x1D709}_{k})P_{k^{\prime }}(1)\equiv _{k}1$
et, par un calcul déjà effectué,
![]() $P_{k^{\prime }}(1)^{-1}P_{k^{\prime }}(-1)\equiv _{k}\operatorname{det}_{k^{\prime }}$
. Soit
$P_{k^{\prime }}(1)^{-1}P_{k^{\prime }}(-1)\equiv _{k}\operatorname{det}_{k^{\prime }}$
. Soit
![]() $k^{\prime }\in K_{i}$
avec
$k^{\prime }\in K_{i}$
avec
![]() $k^{\prime }\not =k$
. Comme précédemment,
$k^{\prime }\not =k$
. Comme précédemment,
![]() $P_{k^{\prime }}(-1)\equiv _{k}1$
. On a
$P_{k^{\prime }}(-1)\equiv _{k}1$
. On a
Pour
![]() $\unicode[STIX]{x1D70E}\in \operatorname{Gal}(F_{k^{\prime }}/F)$
,
$\unicode[STIX]{x1D70E}\in \operatorname{Gal}(F_{k^{\prime }}/F)$
,
![]() $\unicode[STIX]{x1D709}_{k}-\unicode[STIX]{x1D70E}(\unicode[STIX]{x1D709}_{k^{\prime }})$
est congru modulo
$\unicode[STIX]{x1D709}_{k}-\unicode[STIX]{x1D70E}(\unicode[STIX]{x1D709}_{k^{\prime }})$
est congru modulo
![]() $\mathfrak{p}^{\prime }$
à
$\mathfrak{p}^{\prime }$
à
![]() $s_{i}-\unicode[STIX]{x1D70E}(s_{i})$
. Si
$s_{i}-\unicode[STIX]{x1D70E}(s_{i})$
. Si
![]() $\unicode[STIX]{x1D70E}\not \in \operatorname{Gal}(F_{k}/E_{i})$
, ce terme est une unité. Si
$\unicode[STIX]{x1D70E}\not \in \operatorname{Gal}(F_{k}/E_{i})$
, ce terme est une unité. Si
![]() $\unicode[STIX]{x1D70E}\in \operatorname{Gal}(F_{k}/E_{i})$
, on a
$\unicode[STIX]{x1D70E}\in \operatorname{Gal}(F_{k}/E_{i})$
, on a
![]() $\unicode[STIX]{x1D709}_{k}-\unicode[STIX]{x1D70E}(\unicode[STIX]{x1D709}_{k^{\prime }})=s_{i}(E(\unicode[STIX]{x1D6EF}_{k})-\unicode[STIX]{x1D70E}(E(\unicode[STIX]{x1D6EF}_{k^{\prime }})))$
. Notons
$\unicode[STIX]{x1D709}_{k}-\unicode[STIX]{x1D70E}(\unicode[STIX]{x1D709}_{k^{\prime }})=s_{i}(E(\unicode[STIX]{x1D6EF}_{k})-\unicode[STIX]{x1D70E}(E(\unicode[STIX]{x1D6EF}_{k^{\prime }})))$
. Notons
![]() $P_{i,k^{\prime }}$
le polynôme caractéristique de
$P_{i,k^{\prime }}$
le polynôme caractéristique de
![]() $E(\unicode[STIX]{x1D6EF}_{k^{\prime }})$
sur
$E(\unicode[STIX]{x1D6EF}_{k^{\prime }})$
sur
![]() $E_{i}$
. On obtient
$E_{i}$
. On obtient
On calcule ce terme grâce à (8) où l’on remplace le corps
![]() $F$
par
$F$
par
![]() $E_{i}$
. On prend
$E_{i}$
. On prend
![]() $\left(\!\begin{smallmatrix}a & b\\ c & d\end{smallmatrix}\!\right)=\left(\begin{smallmatrix}\frac{1}{2} & 1\\ -\frac{1}{2} & 1\end{smallmatrix}\right)$
,
$\left(\!\begin{smallmatrix}a & b\\ c & d\end{smallmatrix}\!\right)=\left(\begin{smallmatrix}\frac{1}{2} & 1\\ -\frac{1}{2} & 1\end{smallmatrix}\right)$
,
![]() $Z=\unicode[STIX]{x1D6EF}_{k^{\prime }}$
,
$Z=\unicode[STIX]{x1D6EF}_{k^{\prime }}$
,
![]() $T=\unicode[STIX]{x1D6EF}_{k}$
. On obtient
$T=\unicode[STIX]{x1D6EF}_{k}$
. On obtient
d’où
Un même calcul s’applique à
![]() $P_{k}^{\prime }(\unicode[STIX]{x1D709}_{k})P_{k}(-1)$
, en utilisant cette fois la relation (9). D’où
$P_{k}^{\prime }(\unicode[STIX]{x1D709}_{k})P_{k}(-1)$
, en utilisant cette fois la relation (9). D’où
Évidemment,
![]() $(-1)^{n+1}2\unicode[STIX]{x1D709}_{k}^{1-n}(1+\unicode[STIX]{x1D709}_{k})(\unicode[STIX]{x1D709}_{k}-1)^{-1}\equiv _{k}1$
et
$(-1)^{n+1}2\unicode[STIX]{x1D709}_{k}^{1-n}(1+\unicode[STIX]{x1D709}_{k})(\unicode[STIX]{x1D709}_{k}-1)^{-1}\equiv _{k}1$
et
![]() $\unicode[STIX]{x1D702}_{i}\equiv _{k}1$
(tous les termes sont des unités). En rassemblant ces calculs, on obtient
$\unicode[STIX]{x1D702}_{i}\equiv _{k}1$
(tous les termes sont des unités). En rassemblant ces calculs, on obtient
Le produit intervenant ici vaut
![]() $(-1)^{n_{-}}\unicode[STIX]{x1D702}_{-}$
(comme plus haut, on fixe ici un représentant de
$(-1)^{n_{-}}\unicode[STIX]{x1D702}_{-}$
(comme plus haut, on fixe ici un représentant de
![]() $\unicode[STIX]{x1D702}^{-}$
dans
$\unicode[STIX]{x1D702}^{-}$
dans
![]() $F^{\times }$
). Il existe donc
$F^{\times }$
). Il existe donc
![]() $x\in F_{k}^{\times }$
et une unité
$x\in F_{k}^{\times }$
et une unité
![]() $y$
de
$y$
de
![]() $F^{^{\prime }\times }$
tels que
$F^{^{\prime }\times }$
tels que
![]() $C_{k}=y\,\operatorname{norme}_{F_{k}/F_{k}^{\natural }}(x)\unicode[STIX]{x1D702}_{-}\mathfrak{C}_{k}$
. Nécessairement,
$C_{k}=y\,\operatorname{norme}_{F_{k}/F_{k}^{\natural }}(x)\unicode[STIX]{x1D702}_{-}\mathfrak{C}_{k}$
. Nécessairement,
![]() $y$
appartient à
$y$
appartient à
![]() $F_{k}^{\natural ,\times }$
. L’extension
$F_{k}^{\natural ,\times }$
. L’extension
![]() $F_{k}/F_{k}^{\natural }$
est non ramifiée puisque
$F_{k}/F_{k}^{\natural }$
est non ramifiée puisque
![]() $F_{k}$
est le composé de
$F_{k}$
est le composé de
![]() $E_{i}$
et de
$E_{i}$
et de
![]() $F_{k}^{\natural }$
sur
$F_{k}^{\natural }$
sur
![]() $E_{i}^{\natural }$
. Donc
$E_{i}^{\natural }$
. Donc
![]() $\operatorname{sgn}_{k}(y)=1$
, puis
$\operatorname{sgn}_{k}(y)=1$
, puis
![]() $\operatorname{sgn}_{k}(C_{k})=\operatorname{sgn}_{k}(\unicode[STIX]{x1D702}_{-})\operatorname{sgn}_{k}(\mathfrak{C}_{k})$
. Notons
$\operatorname{sgn}_{k}(C_{k})=\operatorname{sgn}_{k}(\unicode[STIX]{x1D702}_{-})\operatorname{sgn}_{k}(\mathfrak{C}_{k})$
. Notons
![]() $\operatorname{val}_{F_{k}^{\natural }}$
la valuation usuelle de
$\operatorname{val}_{F_{k}^{\natural }}$
la valuation usuelle de
![]() $F_{k}^{\natural }$
. On a
$F_{k}^{\natural }$
. On a
![]() $\operatorname{sgn}_{k}(x)=(-1)^{\operatorname{val}_{F_{k}^{\natural }}(x)}$
pour tout
$\operatorname{sgn}_{k}(x)=(-1)^{\operatorname{val}_{F_{k}^{\natural }}(x)}$
pour tout
![]() $x\in F_{k}^{\natural ,\times }$
. En notant
$x\in F_{k}^{\natural ,\times }$
. En notant
![]() $e(F_{k}^{\natural }/F)$
l’indice de ramification de l’extension
$e(F_{k}^{\natural }/F)$
l’indice de ramification de l’extension
![]() $F_{k}^{\natural }/F$
, on a
$F_{k}^{\natural }/F$
, on a
![]() $\operatorname{val}_{F_{k}^{\natural }}(\unicode[STIX]{x1D702}_{-})=e(F_{k}^{\natural }/F)\operatorname{val}_{F}(\unicode[STIX]{x1D702}_{-})$
. Puisque
$\operatorname{val}_{F_{k}^{\natural }}(\unicode[STIX]{x1D702}_{-})=e(F_{k}^{\natural }/F)\operatorname{val}_{F}(\unicode[STIX]{x1D702}_{-})$
. Puisque
![]() $E_{i}^{\natural }/F$
est non ramifiée, on a
$E_{i}^{\natural }/F$
est non ramifiée, on a
où
![]() $f(F_{k}^{\natural }/E_{i}^{\natural })$
est le degré de l’extension résiduelle. Mais
$f(F_{k}^{\natural }/E_{i}^{\natural })$
est le degré de l’extension résiduelle. Mais
![]() $E_{i}$
est l’unique extension quadratique non ramifiée de
$E_{i}$
est l’unique extension quadratique non ramifiée de
![]() $E_{i}^{\natural }$
et elle n’est pas contenue dans
$E_{i}^{\natural }$
et elle n’est pas contenue dans
![]() $F_{k}^{\natural }$
puisque
$F_{k}^{\natural }$
puisque
![]() $F_{k}$
est composé de
$F_{k}$
est composé de
![]() $E_{i}$
et de
$E_{i}$
et de
![]() $F_{k}^{\natural }$
. Donc
$F_{k}^{\natural }$
. Donc
![]() $f(F_{k}^{\natural }/E_{i}^{\natural })$
est impair et
$f(F_{k}^{\natural }/E_{i}^{\natural })$
est impair et
![]() $e(F_{k}^{\natural }/F)$
est de la même parité que
$e(F_{k}^{\natural }/F)$
est de la même parité que
![]() $[F_{k}:E_{i}]$
. D’où
$[F_{k}:E_{i}]$
. D’où
D’où l’égalité (7), ce qui achève la démonstration. ◻
3.2 Calcul d’intégrales orbitales
Fixons
![]() $(r^{\prime },r^{\prime \prime },N^{\prime },N^{\prime \prime })\in \unicode[STIX]{x1D6E4}$
,
$(r^{\prime },r^{\prime \prime },N^{\prime },N^{\prime \prime })\in \unicode[STIX]{x1D6E4}$
,
![]() $w^{\prime }\in W_{N^{\prime }}$
et
$w^{\prime }\in W_{N^{\prime }}$
et
![]() $w^{\prime \prime }\in W_{N^{\prime \prime }}$
. Comme en 2.1, on note
$w^{\prime \prime }\in W_{N^{\prime \prime }}$
. Comme en 2.1, on note
![]() $\unicode[STIX]{x1D711}_{w^{\prime }}$
et
$\unicode[STIX]{x1D711}_{w^{\prime }}$
et
![]() $\unicode[STIX]{x1D711}_{w^{\prime \prime }}$
les fonctions caractéristiques des classes de conjugaison de
$\unicode[STIX]{x1D711}_{w^{\prime \prime }}$
les fonctions caractéristiques des classes de conjugaison de
![]() $w^{\prime }$
et
$w^{\prime }$
et
![]() $w^{\prime \prime }$
. On suppose que ces classes sont paramétrées par des couples de partitions de la forme
$w^{\prime \prime }$
. On suppose que ces classes sont paramétrées par des couples de partitions de la forme
![]() $(\emptyset ,\unicode[STIX]{x1D6FD}^{\prime })$
et
$(\emptyset ,\unicode[STIX]{x1D6FD}^{\prime })$
et
![]() $(\emptyset ,\unicode[STIX]{x1D6FD}^{\prime \prime })$
. On pose
$(\emptyset ,\unicode[STIX]{x1D6FD}^{\prime \prime })$
. On pose
![]() $f=\unicode[STIX]{x1D6F9}\circ k\circ \unicode[STIX]{x1D70C}\unicode[STIX]{x1D704}(\unicode[STIX]{x1D711}_{w^{\prime }}\,\otimes \,\unicode[STIX]{x1D711}_{w^{\prime \prime }})$
, cf. 1.2. On définit un couple d’entiers
$f=\unicode[STIX]{x1D6F9}\circ k\circ \unicode[STIX]{x1D70C}\unicode[STIX]{x1D704}(\unicode[STIX]{x1D711}_{w^{\prime }}\,\otimes \,\unicode[STIX]{x1D711}_{w^{\prime \prime }})$
, cf. 1.2. On définit un couple d’entiers
![]() $(r_{+}^{\prime },r_{-}^{\prime })$
par les égalités
$(r_{+}^{\prime },r_{-}^{\prime })$
par les égalités
![]() $(r_{+}^{\prime },r_{-}^{\prime })=(r^{\prime }+1,r^{\prime })$
, si
$(r_{+}^{\prime },r_{-}^{\prime })=(r^{\prime }+1,r^{\prime })$
, si
![]() $r^{\prime }\equiv r^{\prime \prime }\,\,\text{mod}\,\,2\,\mathbb{Z}$
;
$r^{\prime }\equiv r^{\prime \prime }\,\,\text{mod}\,\,2\,\mathbb{Z}$
;
![]() $(r_{+}^{\prime },r_{-}^{\prime })=(r^{\prime },r^{\prime }+1)$
, si
$(r_{+}^{\prime },r_{-}^{\prime })=(r^{\prime },r^{\prime }+1)$
, si
![]() $r^{\prime }\not \equiv r^{\prime \prime }\,\,\text{mod}\,\,2\,\mathbb{Z}$
.
$r^{\prime }\not \equiv r^{\prime \prime }\,\,\text{mod}\,\,2\,\mathbb{Z}$
.
Soit
![]() $\sharp =\operatorname{iso}$
ou
$\sharp =\operatorname{iso}$
ou
![]() $\operatorname{an}$
et soit
$\operatorname{an}$
et soit
![]() $x\in G_{\sharp }(F)$
un élément elliptique fortement régulier. On l’écrit
$x\in G_{\sharp }(F)$
un élément elliptique fortement régulier. On l’écrit
![]() $x=sE(X)$
et l’on associe à
$x=sE(X)$
et l’on associe à
![]() $s$
les données du paragraphe précédent. En particulier, on a
$s$
les données du paragraphe précédent. En particulier, on a
On considère les hypothèses
(1)(a)
![]() $\operatorname{val}_{F}(\unicode[STIX]{x1D702}_{-})\equiv r^{\prime \prime }\,\,\text{mod}\,\,2\,\mathbb{Z}$
;
$\operatorname{val}_{F}(\unicode[STIX]{x1D702}_{-})\equiv r^{\prime \prime }\,\,\text{mod}\,\,2\,\mathbb{Z}$
;
(1)(b)
![]() $2n_{+}+1\geqslant r_{+}^{\prime 2}+r^{\prime \prime 2}$
,
$2n_{+}+1\geqslant r_{+}^{\prime 2}+r^{\prime \prime 2}$
,
![]() $2n_{-}\geqslant r_{-}^{\prime 2}+r^{\prime \prime 2}$
.
$2n_{-}\geqslant r_{-}^{\prime 2}+r^{\prime \prime 2}$
.
Remarquons que, d’après 3.1(2), la condition (1)(a) équivaut à
![]() $\operatorname{val}_{F}(\unicode[STIX]{x1D702}_{+})\equiv r^{\prime \prime }\,\,\text{mod}\,\,2\,\mathbb{Z}$
.
$\operatorname{val}_{F}(\unicode[STIX]{x1D702}_{+})\equiv r^{\prime \prime }\,\,\text{mod}\,\,2\,\mathbb{Z}$
.
Supposons vérifiées ces conditions (1)(a) et (b). On pose
Notons
![]() $D$
l’ensemble des familles
$D$
l’ensemble des familles
![]() $\mathbf{d}=(N_{+}^{\prime },N_{-}^{\prime },N_{+}^{\prime \prime },N_{-}^{\prime \prime },(d_{i}^{\prime },d_{i}^{\prime \prime })_{i\in I})$
d’entiers positifs ou nuls vérifiant les conditions
$\mathbf{d}=(N_{+}^{\prime },N_{-}^{\prime },N_{+}^{\prime \prime },N_{-}^{\prime \prime },(d_{i}^{\prime },d_{i}^{\prime \prime })_{i\in I})$
d’entiers positifs ou nuls vérifiant les conditions
![]() $d_{i}^{\prime }+d_{i}^{\prime \prime }=d_{i}$
pour tout
$d_{i}^{\prime }+d_{i}^{\prime \prime }=d_{i}$
pour tout
![]() $i\in I$
;
$i\in I$
;
![]() $N_{+}^{\prime }+N_{-}^{\prime }+\sum _{i\in I}d_{i}^{\prime }f_{i}=N^{\prime }$
,
$N_{+}^{\prime }+N_{-}^{\prime }+\sum _{i\in I}d_{i}^{\prime }f_{i}=N^{\prime }$
,
![]() $N_{+}^{\prime \prime }+N_{-}^{\prime \prime }+\sum _{i\in I}d_{i}^{\prime \prime }f_{i}=N^{\prime \prime }$
,
$N_{+}^{\prime \prime }+N_{-}^{\prime \prime }+\sum _{i\in I}d_{i}^{\prime \prime }f_{i}=N^{\prime \prime }$
,
où l’on a posé
![]() $f_{i}=[E_{i}^{\natural }:F]$
. Pour une telle famille, posons
$f_{i}=[E_{i}^{\natural }:F]$
. Pour une telle famille, posons
Considérons l’ensemble des éléments
![]() $\mathbf{v}^{\prime }=(v_{+}^{\prime },v_{-}^{\prime },(v_{i}^{\prime })_{i\in I})\in W^{\prime }(\mathbf{d})$
vérifiant les conditions suivantes :
$\mathbf{v}^{\prime }=(v_{+}^{\prime },v_{-}^{\prime },(v_{i}^{\prime })_{i\in I})\in W^{\prime }(\mathbf{d})$
vérifiant les conditions suivantes :
les classes de conjugaison de
![]() $v_{+}^{\prime }$
et
$v_{+}^{\prime }$
et
![]() $v_{-}^{\prime }$
sont paramétrées par des couples de partitions
$v_{-}^{\prime }$
sont paramétrées par des couples de partitions
![]() $(\emptyset ,\unicode[STIX]{x1D6FD}_{+}^{\prime })$
et
$(\emptyset ,\unicode[STIX]{x1D6FD}_{+}^{\prime })$
et
![]() $(\emptyset ,\unicode[STIX]{x1D6FD}_{-}^{\prime })$
;
$(\emptyset ,\unicode[STIX]{x1D6FD}_{-}^{\prime })$
;
pour
![]() $i\in I$
, la classe de conjugaison de
$i\in I$
, la classe de conjugaison de
![]() $v_{i}^{\prime }$
est paramétrée par une partition
$v_{i}^{\prime }$
est paramétrée par une partition
![]() $\unicode[STIX]{x1D6FD}_{i}^{\prime }$
dont tous les termes non nuls sont impairs ; on note
$\unicode[STIX]{x1D6FD}_{i}^{\prime }$
dont tous les termes non nuls sont impairs ; on note
![]() $f_{i}\unicode[STIX]{x1D6FD}_{i}^{\prime }$
la partition dont les termes sont ceux de
$f_{i}\unicode[STIX]{x1D6FD}_{i}^{\prime }$
la partition dont les termes sont ceux de
![]() $\unicode[STIX]{x1D6FD}_{i}^{\prime }$
multipliés par
$\unicode[STIX]{x1D6FD}_{i}^{\prime }$
multipliés par
![]() $f_{i}$
;
$f_{i}$
;
![]() $\unicode[STIX]{x1D6FD}^{\prime }=\unicode[STIX]{x1D6FD}_{+}^{\prime }\cup \unicode[STIX]{x1D6FD}_{-}^{\prime }\cup \bigcup _{i\in I}f_{i}\unicode[STIX]{x1D6FD}_{i}^{\prime }$
.
$\unicode[STIX]{x1D6FD}^{\prime }=\unicode[STIX]{x1D6FD}_{+}^{\prime }\cup \unicode[STIX]{x1D6FD}_{-}^{\prime }\cup \bigcup _{i\in I}f_{i}\unicode[STIX]{x1D6FD}_{i}^{\prime }$
.
Cet ensemble est une réunion de classes de conjugaison par
![]() $W^{\prime }(\mathbf{d})$
et l’on fixe un ensemble de représentants
$W^{\prime }(\mathbf{d})$
et l’on fixe un ensemble de représentants
![]() ${\mathcal{V}}^{\prime }(\mathbf{d})$
de ces classes. Remarquons que
${\mathcal{V}}^{\prime }(\mathbf{d})$
de ces classes. Remarquons que
(2) pour
![]() $\mathbf{v}^{\prime }=(v_{+}^{\prime },v_{-}^{\prime },(v_{i})_{i\in I})\in W^{\prime }(\mathbf{d})$
, on a l’égalité
$\mathbf{v}^{\prime }=(v_{+}^{\prime },v_{-}^{\prime },(v_{i})_{i\in I})\in W^{\prime }(\mathbf{d})$
, on a l’égalité
En effet,
![]() $\operatorname{sgn}_{CD}(w^{\prime })=(-1)^{l(\unicode[STIX]{x1D6FD}^{\prime })}$
, où
$\operatorname{sgn}_{CD}(w^{\prime })=(-1)^{l(\unicode[STIX]{x1D6FD}^{\prime })}$
, où
![]() $l(\unicode[STIX]{x1D6FD}^{\prime })$
est le nombre de termes non nuls de
$l(\unicode[STIX]{x1D6FD}^{\prime })$
est le nombre de termes non nuls de
![]() $\unicode[STIX]{x1D6FD}^{\prime }$
. On a
$\unicode[STIX]{x1D6FD}^{\prime }$
. On a
![]() $l(\unicode[STIX]{x1D6FD}^{\prime })=l(\unicode[STIX]{x1D6FD}_{+}^{\prime })+l(\unicode[STIX]{x1D6FD}_{-}^{\prime })+\sum _{i\in I}l(\unicode[STIX]{x1D6FD}_{i}^{\prime })$
. Pour
$l(\unicode[STIX]{x1D6FD}^{\prime })=l(\unicode[STIX]{x1D6FD}_{+}^{\prime })+l(\unicode[STIX]{x1D6FD}_{-}^{\prime })+\sum _{i\in I}l(\unicode[STIX]{x1D6FD}_{i}^{\prime })$
. Pour
![]() $i\in I$
,
$i\in I$
,
![]() $\unicode[STIX]{x1D6FD}_{i}^{\prime }$
est une partition de
$\unicode[STIX]{x1D6FD}_{i}^{\prime }$
est une partition de
![]() $d_{i}^{\prime }$
dont tous les termes non nuls sont impairs. Donc
$d_{i}^{\prime }$
dont tous les termes non nuls sont impairs. Donc
![]() $l(\unicode[STIX]{x1D6FD}_{i}^{\prime })\equiv d_{i}^{\prime }\,\,\text{mod}\,\,2\,\mathbb{Z}$
. L’assertion (2) en résulte.
$l(\unicode[STIX]{x1D6FD}_{i}^{\prime })\equiv d_{i}^{\prime }\,\,\text{mod}\,\,2\,\mathbb{Z}$
. L’assertion (2) en résulte.
On pose les mêmes définitions en remplaçant les exposants
![]() $^{\prime }$
par
$^{\prime }$
par
![]() $^{\prime \prime }$
. On pose
$^{\prime \prime }$
. On pose
![]() ${\mathcal{V}}(\mathbf{d})={\mathcal{V}}^{\prime }(\mathbf{d})\times {\mathcal{V}}^{\prime \prime }(\mathbf{d})$
.
${\mathcal{V}}(\mathbf{d})={\mathcal{V}}^{\prime }(\mathbf{d})\times {\mathcal{V}}^{\prime \prime }(\mathbf{d})$
.
Soit
![]() $\mathbf{d}=(N_{+}^{\prime },N_{-}^{\prime },N_{+}^{\prime \prime },N_{-}^{\prime \prime },(d_{i}^{\prime },d_{i}^{\prime \prime })_{i\in I})\in D$
et
$\mathbf{d}=(N_{+}^{\prime },N_{-}^{\prime },N_{+}^{\prime \prime },N_{-}^{\prime \prime },(d_{i}^{\prime },d_{i}^{\prime \prime })_{i\in I})\in D$
et
![]() $\mathbf{v}=(v_{+}^{\prime },v_{-}^{\prime },(v_{i}^{\prime })_{i\in I};v_{+}^{\prime \prime },v_{-}^{\prime \prime },(v_{i}^{\prime \prime })_{i\in I})\in {\mathcal{V}}(\mathbf{d})$
. Supposons que
$\mathbf{v}=(v_{+}^{\prime },v_{-}^{\prime },(v_{i}^{\prime })_{i\in I};v_{+}^{\prime \prime },v_{-}^{\prime \prime },(v_{i}^{\prime \prime })_{i\in I})\in {\mathcal{V}}(\mathbf{d})$
. Supposons que
![]() $n_{+}\geqslant 1$
. Appliquons la construction de 2.1 à l’entier
$n_{+}\geqslant 1$
. Appliquons la construction de 2.1 à l’entier
![]() $n_{+}$
, à l’élément
$n_{+}$
, à l’élément
![]() $\unicode[STIX]{x1D702}_{+}$
et au quadruplet
$\unicode[STIX]{x1D702}_{+}$
et au quadruplet
![]() $(r_{+}^{\prime },|r^{\prime \prime }|,N_{+}^{\prime },N_{+}^{\prime \prime })$
. Les hypothèses de ce paragraphe sont vérifiées d’après (1)(a). On définit deux fonctions
$(r_{+}^{\prime },|r^{\prime \prime }|,N_{+}^{\prime },N_{+}^{\prime \prime })$
. Les hypothèses de ce paragraphe sont vérifiées d’après (1)(a). On définit deux fonctions
![]() $f_{+}^{0}={\mathcal{Q}}_{r_{+}^{\prime },|r^{\prime \prime }|}^{\operatorname{Lie}}\circ \unicode[STIX]{x1D70C}_{N_{+}}^{\ast }\circ \unicode[STIX]{x1D704}_{N_{+}^{\prime },N_{+}^{\prime \prime }}(\unicode[STIX]{x1D711}_{v_{+}^{\prime }}\,\otimes \,\unicode[STIX]{x1D711}_{v_{+}^{\prime \prime }})$
et
$f_{+}^{0}={\mathcal{Q}}_{r_{+}^{\prime },|r^{\prime \prime }|}^{\operatorname{Lie}}\circ \unicode[STIX]{x1D70C}_{N_{+}}^{\ast }\circ \unicode[STIX]{x1D704}_{N_{+}^{\prime },N_{+}^{\prime \prime }}(\unicode[STIX]{x1D711}_{v_{+}^{\prime }}\,\otimes \,\unicode[STIX]{x1D711}_{v_{+}^{\prime \prime }})$
et
![]() $f_{+}^{1}={\mathcal{Q}}_{r_{+}^{\prime },|r^{\prime \prime }|}^{\operatorname{Lie}}\circ \unicode[STIX]{x1D70C}_{N_{+}}^{\ast }\circ \unicode[STIX]{x1D704}_{N_{+}^{\prime \prime },N_{+}^{\prime }}(\unicode[STIX]{x1D711}_{v_{+}^{\prime \prime }}\,\otimes \,\unicode[STIX]{x1D711}_{v_{+}^{\prime }})$
. Elles vivent sur deux algèbres de Lie dont l’une est l’algèbre de Lie
$f_{+}^{1}={\mathcal{Q}}_{r_{+}^{\prime },|r^{\prime \prime }|}^{\operatorname{Lie}}\circ \unicode[STIX]{x1D70C}_{N_{+}}^{\ast }\circ \unicode[STIX]{x1D704}_{N_{+}^{\prime \prime },N_{+}^{\prime }}(\unicode[STIX]{x1D711}_{v_{+}^{\prime \prime }}\,\otimes \,\unicode[STIX]{x1D711}_{v_{+}^{\prime }})$
. Elles vivent sur deux algèbres de Lie dont l’une est l’algèbre de Lie
![]() $\mathfrak{g}_{+}$
de la première composante
$\mathfrak{g}_{+}$
de la première composante
![]() $G_{+}$
de
$G_{+}$
de
![]() $G_{s}$
. En particulier, les intégrales orbitales
$G_{s}$
. En particulier, les intégrales orbitales
![]() $J(X_{+},f_{+}^{0})$
et
$J(X_{+},f_{+}^{0})$
et
![]() $J(X_{+},f_{+}^{1})$
sont bien définies. Supposons que
$J(X_{+},f_{+}^{1})$
sont bien définies. Supposons que
![]() $n_{-}\geqslant 1$
. On applique cette fois la construction de 2.2 et on définit deux fonctions
$n_{-}\geqslant 1$
. On applique cette fois la construction de 2.2 et on définit deux fonctions
![]() $f_{-}^{0}={\mathcal{Q}}_{r_{-}^{\prime },|r^{\prime \prime }|}^{\operatorname{Lie}}\circ \unicode[STIX]{x1D70C}_{N_{-}}^{\ast }\circ \unicode[STIX]{x1D704}_{N_{-}^{\prime },N_{-}^{\prime \prime }}(\unicode[STIX]{x1D711}_{v_{-}^{\prime }}\,\otimes \,\unicode[STIX]{x1D711}_{v_{-}^{\prime \prime }})$
et
$f_{-}^{0}={\mathcal{Q}}_{r_{-}^{\prime },|r^{\prime \prime }|}^{\operatorname{Lie}}\circ \unicode[STIX]{x1D70C}_{N_{-}}^{\ast }\circ \unicode[STIX]{x1D704}_{N_{-}^{\prime },N_{-}^{\prime \prime }}(\unicode[STIX]{x1D711}_{v_{-}^{\prime }}\,\otimes \,\unicode[STIX]{x1D711}_{v_{-}^{\prime \prime }})$
et
![]() $f_{-}^{1}={\mathcal{Q}}_{r_{-}^{\prime },|r^{\prime \prime }|}^{\operatorname{Lie}}\circ \unicode[STIX]{x1D70C}_{N_{-}}^{\ast }\circ \unicode[STIX]{x1D704}_{N_{-}^{\prime \prime },N_{-}^{\prime }}(\unicode[STIX]{x1D711}_{v_{-}^{\prime \prime }}\,\otimes \,\unicode[STIX]{x1D711}_{v_{-}^{\prime }})$
. Les intégrales orbitales
$f_{-}^{1}={\mathcal{Q}}_{r_{-}^{\prime },|r^{\prime \prime }|}^{\operatorname{Lie}}\circ \unicode[STIX]{x1D70C}_{N_{-}}^{\ast }\circ \unicode[STIX]{x1D704}_{N_{-}^{\prime \prime },N_{-}^{\prime }}(\unicode[STIX]{x1D711}_{v_{-}^{\prime \prime }}\,\otimes \,\unicode[STIX]{x1D711}_{v_{-}^{\prime }})$
. Les intégrales orbitales
![]() $J(X_{-},f_{-}^{0})$
et
$J(X_{-},f_{-}^{0})$
et
![]() $J(X_{-},f_{-}^{1})$
sont bien définies. Enfin, pour
$J(X_{-},f_{-}^{1})$
sont bien définies. Enfin, pour
![]() $i\in I$
on utilise les constructions de 2.3. On définit les fonctions
$i\in I$
on utilise les constructions de 2.3. On définit les fonctions
![]() $f_{i}^{0}={\mathcal{Q}}(d_{i}^{\prime },d_{i}^{\prime \prime })^{\operatorname{Lie}}\circ \unicode[STIX]{x1D70C}_{i}^{\ast }\circ \unicode[STIX]{x1D704}_{d_{i}^{\prime },d_{i}^{\prime \prime }}(\unicode[STIX]{x1D711}_{v_{i}^{\prime }}\,\otimes \,\unicode[STIX]{x1D711}_{v_{i}^{\prime \prime }})$
et
$f_{i}^{0}={\mathcal{Q}}(d_{i}^{\prime },d_{i}^{\prime \prime })^{\operatorname{Lie}}\circ \unicode[STIX]{x1D70C}_{i}^{\ast }\circ \unicode[STIX]{x1D704}_{d_{i}^{\prime },d_{i}^{\prime \prime }}(\unicode[STIX]{x1D711}_{v_{i}^{\prime }}\,\otimes \,\unicode[STIX]{x1D711}_{v_{i}^{\prime \prime }})$
et
![]() $f_{i}^{1}={\mathcal{Q}}(d_{i}^{\prime },d_{i}^{\prime \prime })^{\operatorname{Lie}}\circ \unicode[STIX]{x1D70C}_{i}^{\ast }\circ \unicode[STIX]{x1D704}_{d_{i}^{\prime \prime },d_{i}^{\prime }}(\unicode[STIX]{x1D711}_{v_{i}^{\prime \prime }}\,\otimes \,\unicode[STIX]{x1D711}_{v_{i}^{\prime }})$
. Les intégrales orbitales
$f_{i}^{1}={\mathcal{Q}}(d_{i}^{\prime },d_{i}^{\prime \prime })^{\operatorname{Lie}}\circ \unicode[STIX]{x1D70C}_{i}^{\ast }\circ \unicode[STIX]{x1D704}_{d_{i}^{\prime \prime },d_{i}^{\prime }}(\unicode[STIX]{x1D711}_{v_{i}^{\prime \prime }}\,\otimes \,\unicode[STIX]{x1D711}_{v_{i}^{\prime }})$
. Les intégrales orbitales
![]() $J(X_{i},f_{i}^{0})$
et
$J(X_{i},f_{i}^{0})$
et
![]() $J(X_{i},f_{i}^{1})$
sont bien définies. On pose
$J(X_{i},f_{i}^{1})$
sont bien définies. On pose
![]() $f^{0}[\mathbf{d},\mathbf{v}]=f_{+}^{0}\,\otimes \,f_{-}^{0}\,\otimes \,\otimes _{i\in I}f_{i}^{0}$
et
$f^{0}[\mathbf{d},\mathbf{v}]=f_{+}^{0}\,\otimes \,f_{-}^{0}\,\otimes \,\otimes _{i\in I}f_{i}^{0}$
et
Dans ces formules, les termes indexés par
![]() $+$
ou
$+$
ou
![]() $-$
disparaissent si
$-$
disparaissent si
![]() $n_{+}=0$
ou
$n_{+}=0$
ou
![]() $n_{-}=0$
. On définit de même
$n_{-}=0$
. On définit de même
![]() $f^{1}[\mathbf{d},\mathbf{v}]$
et
$f^{1}[\mathbf{d},\mathbf{v}]$
et
![]() $J(X,f^{1}[\mathbf{d},\mathbf{v}])$
. On pose
$J(X,f^{1}[\mathbf{d},\mathbf{v}])$
. On pose
![]() $b=0$
si
$b=0$
si
![]() $r^{\prime \prime }>0$
ou si
$r^{\prime \prime }>0$
ou si
![]() $r^{\prime \prime }=0$
et
$r^{\prime \prime }=0$
et
![]() $r^{\prime }$
est pair ;
$r^{\prime }$
est pair ;
![]() $b=1$
si
$b=1$
si
![]() $r^{\prime \prime }<0$
ou si
$r^{\prime \prime }<0$
ou si
![]() $r^{\prime \prime }=0$
et
$r^{\prime \prime }=0$
et
![]() $r^{\prime }$
est impair.
$r^{\prime }$
est impair.
Posons
 $$\begin{eqnarray}\displaystyle & & \displaystyle c_{\sharp }(r^{\prime },r^{\prime \prime },w^{\prime },w^{\prime \prime })\nonumber\\ \displaystyle & & \displaystyle \quad =\left\{\begin{array}{@{}ll@{}}1, & \text{si}\,\,0<r^{\prime \prime }\leqslant r^{\prime }\,\,\text{ou}\,\,r^{\prime \prime }=0\,\,\text{et}\,\,r^{\prime }\,\,\text{est}\,\operatorname{pair},\\ \operatorname{sgn}_{CD}(w^{\prime \prime }), & \text{si}\,\,r^{\prime }<r^{\prime \prime },\\ \operatorname{sgn}_{\sharp } & \text{si}\,\,-r^{\prime }\leqslant r^{\prime \prime }<0\,\,\text{ou}\,\,r^{\prime \prime }=0\,\,\text{et}\,\,r^{\prime }\,\,\text{est}\,\operatorname{impair},\\ \operatorname{sgn}_{\sharp }\operatorname{sgn}_{CD}(w^{\prime }), & \text{si}\,\,r^{\prime \prime }<-r^{\prime }.\end{array}\right.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle c_{\sharp }(r^{\prime },r^{\prime \prime },w^{\prime },w^{\prime \prime })\nonumber\\ \displaystyle & & \displaystyle \quad =\left\{\begin{array}{@{}ll@{}}1, & \text{si}\,\,0<r^{\prime \prime }\leqslant r^{\prime }\,\,\text{ou}\,\,r^{\prime \prime }=0\,\,\text{et}\,\,r^{\prime }\,\,\text{est}\,\operatorname{pair},\\ \operatorname{sgn}_{CD}(w^{\prime \prime }), & \text{si}\,\,r^{\prime }<r^{\prime \prime },\\ \operatorname{sgn}_{\sharp } & \text{si}\,\,-r^{\prime }\leqslant r^{\prime \prime }<0\,\,\text{ou}\,\,r^{\prime \prime }=0\,\,\text{et}\,\,r^{\prime }\,\,\text{est}\,\operatorname{impair},\\ \operatorname{sgn}_{\sharp }\operatorname{sgn}_{CD}(w^{\prime }), & \text{si}\,\,r^{\prime \prime }<-r^{\prime }.\end{array}\right.\nonumber\end{eqnarray}$$
Proposition.
(i) Si les hypothèses (1)(a) et (1)(b) ne sont pas vérifiées,
 $J(x,f)=0$
.
$J(x,f)=0$
.(ii) Supposons ces hypothèses vérifiées. Alors on a l’égalité
 $$\begin{eqnarray}J(x,f)=c(r^{\prime },r^{\prime \prime })c_{\sharp }(r^{\prime },r^{\prime \prime },w^{\prime },w^{\prime \prime })\mathop{\sum }_{\mathbf{d}\in D}\mathop{\sum }_{\mathbf{v}\in {\mathcal{V}}(\mathbf{d})}J(X,f^{b}[\mathbf{d},\mathbf{v}]).\end{eqnarray}$$
$$\begin{eqnarray}J(x,f)=c(r^{\prime },r^{\prime \prime })c_{\sharp }(r^{\prime },r^{\prime \prime },w^{\prime },w^{\prime \prime })\mathop{\sum }_{\mathbf{d}\in D}\mathop{\sum }_{\mathbf{v}\in {\mathcal{V}}(\mathbf{d})}J(X,f^{b}[\mathbf{d},\mathbf{v}]).\end{eqnarray}$$
C’est la proposition 3.19 de [Reference Moeglin and Waldspurger6].
3.3 Démonstration du (ii) de la proposition 1.2
On conserve les données
![]() $(r^{\prime },r^{\prime \prime },N^{\prime },N^{\prime \prime })\in \unicode[STIX]{x1D6E4}$
,
$(r^{\prime },r^{\prime \prime },N^{\prime },N^{\prime \prime })\in \unicode[STIX]{x1D6E4}$
,
![]() $w^{\prime }\in W_{N^{\prime }}$
et
$w^{\prime }\in W_{N^{\prime }}$
et
![]() $w^{\prime \prime }\in W_{N^{\prime \prime }}$
. On définit
$w^{\prime \prime }\in W_{N^{\prime \prime }}$
. On définit
![]() $f$
comme dans le paragraphe précédent.
$f$
comme dans le paragraphe précédent.
Soit
![]() $(n_{1},n_{2})\in D(n)$
, auquel est associée une donnée endoscopique de
$(n_{1},n_{2})\in D(n)$
, auquel est associée une donnée endoscopique de
![]() $G_{\operatorname{iso}}$
et
$G_{\operatorname{iso}}$
et
![]() $G_{\operatorname{an}}$
dont le groupe endoscopique est
$G_{\operatorname{an}}$
dont le groupe endoscopique est
![]() $G_{n_{1},\operatorname{iso}}\times G_{n_{2},\operatorname{iso}}$
. Soit
$G_{n_{1},\operatorname{iso}}\times G_{n_{2},\operatorname{iso}}$
. Soit
![]() $(x_{1},x_{2})\in G_{n_{1},\operatorname{iso}}(F)\times G_{n_{2},\operatorname{iso}}(F)$
un couple
$(x_{1},x_{2})\in G_{n_{1},\operatorname{iso}}(F)\times G_{n_{2},\operatorname{iso}}(F)$
un couple
![]() $n$
-régulier formé d’éléments elliptiques. On lui associe les données du paragraphe 3.1 :
$n$
-régulier formé d’éléments elliptiques. On lui associe les données du paragraphe 3.1 :
![]() $n_{1,+}$
,
$n_{1,+}$
,
![]() $\unicode[STIX]{x1D702}_{1,+}$
, etc. À un élément quelconque de la classe totale de conjugaison stable dans
$\unicode[STIX]{x1D702}_{1,+}$
, etc. À un élément quelconque de la classe totale de conjugaison stable dans
![]() $G_{\operatorname{iso}}(F)\cup G_{\operatorname{an}}(F)$
correspondant à
$G_{\operatorname{iso}}(F)\cup G_{\operatorname{an}}(F)$
correspondant à
![]() $(x_{1},x_{2})$
sont aussi associées des données
$(x_{1},x_{2})$
sont aussi associées des données
![]() $n_{+}$
,
$n_{+}$
,
![]() $\unicode[STIX]{x1D702}_{+}$
, etc. On va calculer
$\unicode[STIX]{x1D702}_{+}$
, etc. On va calculer
où
![]() $x$
décrit cette classe totale de conjugaison stable, à conjugaison près. Les intégrales orbitales
$x$
décrit cette classe totale de conjugaison stable, à conjugaison près. Les intégrales orbitales
![]() $J(x,f)$
sont calculées par la proposition précédente. On en déduit immédiatement
$J(x,f)$
sont calculées par la proposition précédente. On en déduit immédiatement
(1) si les hypothèses (1)(a) et (b) de 3.2 ne sont pas vérifiées,
![]() $J^{\operatorname{endo}}(x_{1},x_{2},f)=0$
.
$J^{\operatorname{endo}}(x_{1},x_{2},f)=0$
.
Supposons ces hypothèses vérifiées. Comme on l’a expliqué en 3.1, l’application
![]() $x\mapsto X$
identifie la sommation à la somme sur les
$x\mapsto X$
identifie la sommation à la somme sur les
![]() $X\in \mathfrak{g}_{\operatorname{iso}}(F)\cup \mathfrak{g}_{\operatorname{an}}(F)$
dans la classe totale de conjugaison stable correspondant à celle de
$X\in \mathfrak{g}_{\operatorname{iso}}(F)\cup \mathfrak{g}_{\operatorname{an}}(F)$
dans la classe totale de conjugaison stable correspondant à celle de
![]() $(X_{1},X_{2})$
. Le lemme 3.1 et la proposition 3.2 expriment les termes
$(X_{1},X_{2})$
. Le lemme 3.1 et la proposition 3.2 expriment les termes
![]() $\unicode[STIX]{x1D6E5}((x_{1},x_{2}),x)$
et
$\unicode[STIX]{x1D6E5}((x_{1},x_{2}),x)$
et
![]() $J(x,f)$
à l’aide de l’élément
$J(x,f)$
à l’aide de l’élément
![]() $X$
, à l’exception de la constante
$X$
, à l’exception de la constante
![]() $c_{\sharp }(r^{\prime },r^{\prime \prime },w^{\prime },w^{\prime \prime })$
car l’indice
$c_{\sharp }(r^{\prime },r^{\prime \prime },w^{\prime },w^{\prime \prime })$
car l’indice
![]() $\sharp$
est celui tel que
$\sharp$
est celui tel que
![]() $x$
appartienne à
$x$
appartienne à
![]() $G_{\sharp }(F)$
. Mais la relation 3.1(3) calcule cet indice à l’aide de
$G_{\sharp }(F)$
. Mais la relation 3.1(3) calcule cet indice à l’aide de
![]() $X$
. Remarquons que, dans cette relation, on peut remplacer
$X$
. Remarquons que, dans cette relation, on peut remplacer
![]() $\operatorname{val}_{F}(\unicode[STIX]{x1D702}_{-})$
par
$\operatorname{val}_{F}(\unicode[STIX]{x1D702}_{-})$
par
![]() $r^{\prime \prime }$
d’après l’hypothèse (1)(a) de 3.2. Rappelons que
$r^{\prime \prime }$
d’après l’hypothèse (1)(a) de 3.2. Rappelons que
![]() $b=0$
si
$b=0$
si
![]() $r^{\prime \prime }>0$
ou si
$r^{\prime \prime }>0$
ou si
![]() $r^{\prime \prime }=0$
et
$r^{\prime \prime }=0$
et
![]() $r^{\prime }$
est pair, et
$r^{\prime }$
est pair, et
![]() $b=1$
si
$b=1$
si
![]() $r^{\prime \prime }<0$
ou si
$r^{\prime \prime }<0$
ou si
![]() $r^{\prime \prime }=0$
et
$r^{\prime \prime }=0$
et
![]() $r^{\prime }$
est impair. Définissons
$r^{\prime }$
est impair. Définissons
 $$\begin{eqnarray}\displaystyle & & \displaystyle c(r^{\prime },r^{\prime \prime },w^{\prime },w^{\prime \prime })\nonumber\\ \displaystyle & & \displaystyle \quad =\left\{\begin{array}{@{}ll@{}}1, & \text{si}\,\,0<r^{\prime \prime }\leqslant r^{\prime }\,\,\text{ou}\,\,r^{\prime \prime }=0\,\,\text{et}\,\,r^{\prime }\,\,est\,\operatorname{pair},\\ \operatorname{sgn}_{CD}(w^{\prime \prime }), & \text{si}\,\,r^{\prime }<r^{\prime \prime },\\ (-1)^{dr^{\prime \prime }} & \text{si}\,\,-r^{\prime }\leqslant r^{\prime \prime }<0\,\,\text{ou}\,\,r^{\prime \prime }=0\,\,\text{et}\,\,r^{\prime }\,\,\text{est}\,\operatorname{impair},\\ (-1)^{dr^{\prime \prime }}\operatorname{sgn}_{CD}(w^{\prime }), & \text{si}\,\,r^{\prime \prime }<-r^{\prime }.\end{array}\right.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle c(r^{\prime },r^{\prime \prime },w^{\prime },w^{\prime \prime })\nonumber\\ \displaystyle & & \displaystyle \quad =\left\{\begin{array}{@{}ll@{}}1, & \text{si}\,\,0<r^{\prime \prime }\leqslant r^{\prime }\,\,\text{ou}\,\,r^{\prime \prime }=0\,\,\text{et}\,\,r^{\prime }\,\,est\,\operatorname{pair},\\ \operatorname{sgn}_{CD}(w^{\prime \prime }), & \text{si}\,\,r^{\prime }<r^{\prime \prime },\\ (-1)^{dr^{\prime \prime }} & \text{si}\,\,-r^{\prime }\leqslant r^{\prime \prime }<0\,\,\text{ou}\,\,r^{\prime \prime }=0\,\,\text{et}\,\,r^{\prime }\,\,\text{est}\,\operatorname{impair},\\ (-1)^{dr^{\prime \prime }}\operatorname{sgn}_{CD}(w^{\prime }), & \text{si}\,\,r^{\prime \prime }<-r^{\prime }.\end{array}\right.\nonumber\end{eqnarray}$$
On a alors l’égalité
On peut aussi remplacer
![]() $(-1)^{d_{2}\operatorname{val}_{F}(\unicode[STIX]{x1D702}_{-})}$
par
$(-1)^{d_{2}\operatorname{val}_{F}(\unicode[STIX]{x1D702}_{-})}$
par
![]() $(-1)^{dr^{\prime \prime }}$
dans l’énoncé du lemme 3.1. Alors ce lemme et la proposition 3.2 entraînent l’égalité
$(-1)^{dr^{\prime \prime }}$
dans l’énoncé du lemme 3.1. Alors ce lemme et la proposition 3.2 entraînent l’égalité
 $$\begin{eqnarray}\displaystyle J^{\operatorname{endo}}(x_{1},x_{2},f) & = & \displaystyle c(r^{\prime },r^{\prime \prime })c(r^{\prime },r^{\prime \prime },w^{\prime },w^{\prime \prime })(-1)^{d_{2}r^{\prime \prime }}\mathop{\sum }_{\mathbf{d}\in D}\mathop{\sum }_{\mathbf{v}\in {\mathcal{V}}(\mathbf{d})}\nonumber\\ \displaystyle & & \displaystyle \times \,\mathop{\sum }_{X}\unicode[STIX]{x1D6E5}((X_{1},X_{2}),X)\operatorname{sgn}^{\ast }(X)^{b}J(X,f^{b}[\mathbf{d},\mathbf{v}]).\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle J^{\operatorname{endo}}(x_{1},x_{2},f) & = & \displaystyle c(r^{\prime },r^{\prime \prime })c(r^{\prime },r^{\prime \prime },w^{\prime },w^{\prime \prime })(-1)^{d_{2}r^{\prime \prime }}\mathop{\sum }_{\mathbf{d}\in D}\mathop{\sum }_{\mathbf{v}\in {\mathcal{V}}(\mathbf{d})}\nonumber\\ \displaystyle & & \displaystyle \times \,\mathop{\sum }_{X}\unicode[STIX]{x1D6E5}((X_{1},X_{2}),X)\operatorname{sgn}^{\ast }(X)^{b}J(X,f^{b}[\mathbf{d},\mathbf{v}]).\end{eqnarray}$$
Fixons
![]() $\mathbf{d}\in D$
et
$\mathbf{d}\in D$
et
![]() $\mathbf{v}\in {\mathcal{V}}(\mathbf{d})$
. On a par définition une décomposition
$\mathbf{v}\in {\mathcal{V}}(\mathbf{d})$
. On a par définition une décomposition
![]() $f^{b}[\mathbf{d},\mathbf{v}]=f_{+}^{b}\,\otimes \,f_{-}^{b}\,\otimes \,\otimes _{i\in I}f_{i}^{b}$
. Posons
$f^{b}[\mathbf{d},\mathbf{v}]=f_{+}^{b}\,\otimes \,f_{-}^{b}\,\otimes \,\otimes _{i\in I}f_{i}^{b}$
. Posons
où
![]() $X_{+}$
parcourt la classe totale de conjugaison stable correspondant à celle de
$X_{+}$
parcourt la classe totale de conjugaison stable correspondant à celle de
![]() $(X_{1,+},X_{2,+})$
. On définit de même
$(X_{1,+},X_{2,+})$
. On définit de même
![]() $J^{\operatorname{endo},\ast }(X_{1,-},X_{2,-},f_{-}^{b})$
et
$J^{\operatorname{endo},\ast }(X_{1,-},X_{2,-},f_{-}^{b})$
et
![]() $J^{\operatorname{endo},\ast }(X_{1,i},X_{2,i},f_{i}^{b})$
pour
$J^{\operatorname{endo},\ast }(X_{1,i},X_{2,i},f_{i}^{b})$
pour
![]() $i\in I$
. La somme en
$i\in I$
. La somme en
![]() $X$
de l’expression (2) est égale à
$X$
de l’expression (2) est égale à
Supposons d’abord que
![]() $b=0$
. Alors
$b=0$
. Alors
![]() $\operatorname{sgn}^{\ast }(X_{+})^{b}$
disparaît de la définition de
$\operatorname{sgn}^{\ast }(X_{+})^{b}$
disparaît de la définition de
![]() $J^{\operatorname{endo},\ast }(X_{1,+},X_{2,+},f_{+}^{b})$
et ce terme est l’intégrale endoscopique
$J^{\operatorname{endo},\ast }(X_{1,+},X_{2,+},f_{+}^{b})$
et ce terme est l’intégrale endoscopique
![]() $J^{\operatorname{endo}}(X_{1,+},X_{2,+},f_{+}^{0})$
. De même pour les autres termes de (3). On applique les (ii) des lemmes 2.1, 2.2 et 2.3 ; le produit de ces intégrales endoscopiques est nul sauf si les conditions suivantes sont vérifiées :
$J^{\operatorname{endo}}(X_{1,+},X_{2,+},f_{+}^{0})$
. De même pour les autres termes de (3). On applique les (ii) des lemmes 2.1, 2.2 et 2.3 ; le produit de ces intégrales endoscopiques est nul sauf si les conditions suivantes sont vérifiées :
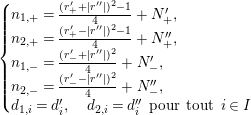 $$\begin{eqnarray}\left\{\begin{array}{@{}l@{}}n_{1,+}=\frac{(r_{+}^{\prime }+|r^{\prime \prime }|)^{2}-1}{4}+N_{+}^{\prime },\\ n_{2,+}=\frac{(r_{+}^{\prime }-|r^{\prime \prime }|)^{2}-1}{4}+N_{+}^{\prime \prime },\\ n_{1,-}=\frac{(r_{-}^{\prime }+|r^{\prime \prime }|)^{2}}{4}+N_{-}^{\prime },\\ n_{2,-}=\frac{(r_{-}^{\prime }-|r^{\prime \prime }|)^{2}}{4}+N_{-}^{\prime \prime },\\ d_{1,i}=d_{i}^{\prime },\quad d_{2,i}=d_{i}^{\prime \prime }\,\,\text{pour}\,\,\text{tout}\,\,i\in I\end{array}\right.\end{eqnarray}$$
$$\begin{eqnarray}\left\{\begin{array}{@{}l@{}}n_{1,+}=\frac{(r_{+}^{\prime }+|r^{\prime \prime }|)^{2}-1}{4}+N_{+}^{\prime },\\ n_{2,+}=\frac{(r_{+}^{\prime }-|r^{\prime \prime }|)^{2}-1}{4}+N_{+}^{\prime \prime },\\ n_{1,-}=\frac{(r_{-}^{\prime }+|r^{\prime \prime }|)^{2}}{4}+N_{-}^{\prime },\\ n_{2,-}=\frac{(r_{-}^{\prime }-|r^{\prime \prime }|)^{2}}{4}+N_{-}^{\prime \prime },\\ d_{1,i}=d_{i}^{\prime },\quad d_{2,i}=d_{i}^{\prime \prime }\,\,\text{pour}\,\,\text{tout}\,\,i\in I\end{array}\right.\end{eqnarray}$$
(5)
![]() $\operatorname{val}_{F}(\unicode[STIX]{x1D702}_{1,-})\equiv \frac{r_{-}^{\prime }+|r^{\prime \prime }|}{2}\,\,\text{mod}\,\,2\,\mathbb{Z}$
,
$\operatorname{val}_{F}(\unicode[STIX]{x1D702}_{1,-})\equiv \frac{r_{-}^{\prime }+|r^{\prime \prime }|}{2}\,\,\text{mod}\,\,2\,\mathbb{Z}$
,
![]() $\operatorname{val}_{F}(\unicode[STIX]{x1D702}_{2,-})\equiv \frac{r_{-}^{\prime }-|r^{\prime \prime }|}{2}\,\,\text{mod}\,\,2\,\mathbb{Z}$
.
$\operatorname{val}_{F}(\unicode[STIX]{x1D702}_{2,-})\equiv \frac{r_{-}^{\prime }-|r^{\prime \prime }|}{2}\,\,\text{mod}\,\,2\,\mathbb{Z}$
.
Notre hypothèse
![]() $b=0$
implique que
$b=0$
implique que
![]() $|r^{\prime \prime }|=r^{\prime \prime }$
. Pour
$|r^{\prime \prime }|=r^{\prime \prime }$
. Pour
![]() $j=1,2$
, on a
$j=1,2$
, on a
![]() $n_{j}=n_{j,+}+n_{j,-}+\sum _{i\in I}f_{i}d_{j,i}$
. En utilisant l’égalité
$n_{j}=n_{j,+}+n_{j,-}+\sum _{i\in I}f_{i}d_{j,i}$
. En utilisant l’égalité
![]() $\{r_{+}^{\prime },r_{-}^{\prime }\}=\{r^{\prime },r^{\prime }+1\}$
et le fait que
$\{r_{+}^{\prime },r_{-}^{\prime }\}=\{r^{\prime },r^{\prime }+1\}$
et le fait que
![]() $\mathbf{d}\in D$
, la condition (4) ci-dessus implique
$\mathbf{d}\in D$
, la condition (4) ci-dessus implique
 $$\begin{eqnarray}\displaystyle n_{1} & = & \displaystyle \frac{(r^{\prime }+r^{\prime \prime })^{2}+(r^{\prime }+r^{\prime \prime }+1)^{2}-1}{4}+N^{\prime },\nonumber\\ \displaystyle n_{2} & = & \displaystyle \frac{(r^{\prime }-r^{\prime \prime })^{2}+(r^{\prime }-r^{\prime \prime }+1)^{2}-1}{4}+N^{\prime \prime }.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle n_{1} & = & \displaystyle \frac{(r^{\prime }+r^{\prime \prime })^{2}+(r^{\prime }+r^{\prime \prime }+1)^{2}-1}{4}+N^{\prime },\nonumber\\ \displaystyle n_{2} & = & \displaystyle \frac{(r^{\prime }-r^{\prime \prime })^{2}+(r^{\prime }-r^{\prime \prime }+1)^{2}-1}{4}+N^{\prime \prime }.\nonumber\end{eqnarray}$$
C’est précisément le couple
![]() $(n_{1},n_{2})$
défini en 1.2. Cela prouve que si notre couple
$(n_{1},n_{2})$
défini en 1.2. Cela prouve que si notre couple
![]() $(n_{1},n_{2})$
n’est pas celui défini dans ce paragraphe, (3) est nul. Cela étant vrai pour tous
$(n_{1},n_{2})$
n’est pas celui défini dans ce paragraphe, (3) est nul. Cela étant vrai pour tous
![]() $\mathbf{d}$
,
$\mathbf{d}$
,
![]() $\mathbf{v}$
, on a
$\mathbf{v}$
, on a
![]() $J^{\operatorname{endo}}(x_{1},x_{2},f)=0$
d’après (2). Cela étant vrai pour tout
$J^{\operatorname{endo}}(x_{1},x_{2},f)=0$
d’après (2). Cela étant vrai pour tout
![]() $(x_{1},x_{2})$
, le transfert de
$(x_{1},x_{2})$
, le transfert de
![]() $f$
relatif à
$f$
relatif à
![]() $(n_{1},n_{2})$
est nul.
$(n_{1},n_{2})$
est nul.
Supposons maintenant que
![]() $b=1$
. Le couple
$b=1$
. Le couple
![]() $(n_{1,+},n_{2,+})$
définit une donnée endoscopique pour les deux groupes spéciaux orthogonaux impairs dont les algèbres de Lie contiennent nos éléments
$(n_{1,+},n_{2,+})$
définit une donnée endoscopique pour les deux groupes spéciaux orthogonaux impairs dont les algèbres de Lie contiennent nos éléments
![]() $X_{+}$
. Le couple
$X_{+}$
. Le couple
![]() $(n_{2,+},n_{1,+})$
définit aussi une telle donnée. On a donc également un facteur de transfert
$(n_{2,+},n_{1,+})$
définit aussi une telle donnée. On a donc également un facteur de transfert
![]() $\unicode[STIX]{x1D6E5}_{+}((X_{2,+},X_{1,+}),X_{+})$
. Comme on l’a dit en [Reference Waldspurger11] 2.1, on a l’égalité
$\unicode[STIX]{x1D6E5}_{+}((X_{2,+},X_{1,+}),X_{+})$
. Comme on l’a dit en [Reference Waldspurger11] 2.1, on a l’égalité
On voit alors que
![]() $J^{\operatorname{endo},\ast }(X_{1,+},X_{2,+},f_{+}^{b})=J^{\operatorname{endo}}(X_{2,+},X_{1,+},f_{+}^{1})$
. De même pour les autres termes de (3). Le raisonnement se poursuit comme ci-dessus. On permute les rôles des indices
$J^{\operatorname{endo},\ast }(X_{1,+},X_{2,+},f_{+}^{b})=J^{\operatorname{endo}}(X_{2,+},X_{1,+},f_{+}^{1})$
. De même pour les autres termes de (3). Le raisonnement se poursuit comme ci-dessus. On permute les rôles des indices
![]() $1$
et
$1$
et
![]() $2$
; on permute aussi
$2$
; on permute aussi
![]() $N^{\prime }$
et
$N^{\prime }$
et
![]() $N^{\prime \prime }$
puisque l’on remplace la fonction
$N^{\prime \prime }$
puisque l’on remplace la fonction
![]() $f^{0}[\mathbf{d},\mathbf{v}]$
par
$f^{0}[\mathbf{d},\mathbf{v}]$
par
![]() $f^{1}[\mathbf{d},\mathbf{v}]$
; enfin, l’hypothèse
$f^{1}[\mathbf{d},\mathbf{v}]$
; enfin, l’hypothèse
![]() $b=1$
entraîne que
$b=1$
entraîne que
![]() $|r^{\prime \prime }|=-r^{\prime \prime }$
. Ces trois modifications conduisent au même résultat : le transfert de
$|r^{\prime \prime }|=-r^{\prime \prime }$
. Ces trois modifications conduisent au même résultat : le transfert de
![]() $f$
relatif à
$f$
relatif à
![]() $(n_{1},n_{2})$
est nul si
$(n_{1},n_{2})$
est nul si
![]() $(n_{1},n_{2})$
n’est pas le couple défini en 1.2. Cela démontre le (ii) de la proposition 1.2 pour les fonctions
$(n_{1},n_{2})$
n’est pas le couple défini en 1.2. Cela démontre le (ii) de la proposition 1.2 pour les fonctions
![]() $\unicode[STIX]{x1D711}^{\prime }=\unicode[STIX]{x1D711}_{w^{\prime }}$
et
$\unicode[STIX]{x1D711}^{\prime }=\unicode[STIX]{x1D711}_{w^{\prime }}$
et
![]() $\unicode[STIX]{x1D711}^{\prime \prime }=\unicode[STIX]{x1D711}_{w^{\prime \prime }}$
. En faisant varier
$\unicode[STIX]{x1D711}^{\prime \prime }=\unicode[STIX]{x1D711}_{w^{\prime \prime }}$
. En faisant varier
![]() $w^{\prime }$
et
$w^{\prime }$
et
![]() $w^{\prime \prime }$
, cela démontre cette assertion pour toutes fonctions cuspidales
$w^{\prime \prime }$
, cela démontre cette assertion pour toutes fonctions cuspidales
![]() $\unicode[STIX]{x1D711}^{\prime }$
et
$\unicode[STIX]{x1D711}^{\prime }$
et
![]() $\unicode[STIX]{x1D711}^{\prime \prime }$
.
$\unicode[STIX]{x1D711}^{\prime \prime }$
.
3.4 Démonstration du (i) de la proposition 1.2
On poursuit le calcul précédent en supposant que
![]() $(n_{1},n_{2})$
est le couple défini en 1.2. On suppose vérifiées les hypothèses (1)(a) et (1)(b) de 3.2. On fixe
$(n_{1},n_{2})$
est le couple défini en 1.2. On suppose vérifiées les hypothèses (1)(a) et (1)(b) de 3.2. On fixe
![]() $\mathbf{d}\in D$
et
$\mathbf{d}\in D$
et
![]() $\mathbf{v}\in {\mathcal{V}}(\mathbf{d})$
. On suppose d’abord que
$\mathbf{v}\in {\mathcal{V}}(\mathbf{d})$
. On suppose d’abord que
![]() $b=0$
. Comme on l’a expliqué, la somme en
$b=0$
. Comme on l’a expliqué, la somme en
![]() $X$
de 3.3(2) est égale à
$X$
de 3.3(2) est égale à
Ce produit est nul sauf si les conditions (4) et (5) de 3.3 sont vérifiées. L’hypothèse (5) est indépendante de
![]() $\mathbf{d}$
et
$\mathbf{d}$
et
![]() $\mathbf{v}$
. Récrivons-la (en se rappelant que
$\mathbf{v}$
. Récrivons-la (en se rappelant que
![]() $r^{\prime \prime }\geqslant 0$
puisque
$r^{\prime \prime }\geqslant 0$
puisque
![]() $b=0$
) :
$b=0$
) :
(2)
![]() $\operatorname{val}_{F}(\unicode[STIX]{x1D702}_{1,-})\equiv \frac{r_{-}^{\prime }+r^{\prime \prime }}{2}\,\,\text{mod}\,\,2\,\mathbb{Z}$
,
$\operatorname{val}_{F}(\unicode[STIX]{x1D702}_{1,-})\equiv \frac{r_{-}^{\prime }+r^{\prime \prime }}{2}\,\,\text{mod}\,\,2\,\mathbb{Z}$
,
![]() $\operatorname{val}_{F}(\unicode[STIX]{x1D702}_{2,-})\equiv \frac{r_{-}^{\prime }-r^{\prime \prime }}{2}\,\,\text{mod}\,\,2\,\mathbb{Z}$
.
$\operatorname{val}_{F}(\unicode[STIX]{x1D702}_{2,-})\equiv \frac{r_{-}^{\prime }-r^{\prime \prime }}{2}\,\,\text{mod}\,\,2\,\mathbb{Z}$
.
Puisque
![]() $\unicode[STIX]{x1D702}_{-}=\unicode[STIX]{x1D702}_{1,-}\unicode[STIX]{x1D702}_{2,-}$
, elle implique l’hypothèse (1)(a) de 3.2. Si l’hypothèse (4) de 3.3 est vérifiée, on a les inégalités
$\unicode[STIX]{x1D702}_{-}=\unicode[STIX]{x1D702}_{1,-}\unicode[STIX]{x1D702}_{2,-}$
, elle implique l’hypothèse (1)(a) de 3.2. Si l’hypothèse (4) de 3.3 est vérifiée, on a les inégalités
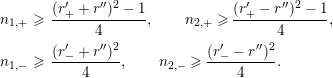 $$\begin{eqnarray}\displaystyle n_{1,+} & {\geqslant} & \displaystyle \frac{(r_{+}^{\prime }+r^{\prime \prime })^{2}-1}{4},\qquad n_{2,+}\geqslant \frac{(r_{+}^{\prime }-r^{\prime \prime })^{2}-1}{4},\nonumber\\ \displaystyle n_{1,-} & {\geqslant} & \displaystyle \frac{(r_{-}^{\prime }+r^{\prime \prime })^{2}}{4},\qquad n_{2,-}\geqslant \frac{(r_{-}^{\prime }-r^{\prime \prime })^{2}}{4}.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle n_{1,+} & {\geqslant} & \displaystyle \frac{(r_{+}^{\prime }+r^{\prime \prime })^{2}-1}{4},\qquad n_{2,+}\geqslant \frac{(r_{+}^{\prime }-r^{\prime \prime })^{2}-1}{4},\nonumber\\ \displaystyle n_{1,-} & {\geqslant} & \displaystyle \frac{(r_{-}^{\prime }+r^{\prime \prime })^{2}}{4},\qquad n_{2,-}\geqslant \frac{(r_{-}^{\prime }-r^{\prime \prime })^{2}}{4}.\end{eqnarray}$$
Puisque
![]() $n_{+}=n_{1,+}+n_{2,+}$
,
$n_{+}=n_{1,+}+n_{2,+}$
,
![]() $n_{-}=n_{1,-}+n_{2,-}$
, ces inégalités impliquent l’hypothèse (1)(b) de 3.2. On peut donc oublier les hypothèses (1)(a) et (b) de 3.2 et supposer vérifiées les hypothèses (2) et (3) ci-dessus. Alors les relations (4) de 3.3 déterminent un unique élément
$n_{-}=n_{1,-}+n_{2,-}$
, ces inégalités impliquent l’hypothèse (1)(b) de 3.2. On peut donc oublier les hypothèses (1)(a) et (b) de 3.2 et supposer vérifiées les hypothèses (2) et (3) ci-dessus. Alors les relations (4) de 3.3 déterminent un unique élément
![]() $\mathbf{d}$
dont l’on vérifie qu’il appartient bien à
$\mathbf{d}$
dont l’on vérifie qu’il appartient bien à
![]() $D$
. On suppose désormais que
$D$
. On suppose désormais que
![]() $\mathbf{d}$
est cet unique élément.
$\mathbf{d}$
est cet unique élément.
L’intégrale endoscopique
![]() $J^{\operatorname{endo}}(X_{1,+},X_{2,+},f_{+}^{0})$
est calculée par le lemme 2.1. Adaptons les notations. On note
$J^{\operatorname{endo}}(X_{1,+},X_{2,+},f_{+}^{0})$
est calculée par le lemme 2.1. Adaptons les notations. On note
![]() $t_{1,+}^{\prime },t_{1,+}^{\prime \prime },t_{2,+}^{\prime }$
et
$t_{1,+}^{\prime },t_{1,+}^{\prime \prime },t_{2,+}^{\prime }$
et
![]() $t_{2,+}^{\prime \prime }$
les termes notés
$t_{2,+}^{\prime \prime }$
les termes notés
![]() $t_{1}^{\prime }$
, etc., en 2.1 associés à
$t_{1}^{\prime }$
, etc., en 2.1 associés à
![]() $n_{+}$
,
$n_{+}$
,
![]() $r_{+}^{\prime }$
et
$r_{+}^{\prime }$
et
![]() $|r^{\prime \prime }|$
. On note
$|r^{\prime \prime }|$
. On note
![]() $C_{+}(\mathbf{v})$
la constante
$C_{+}(\mathbf{v})$
la constante
![]() $C$
de 2.2. On pose
$C$
de 2.2. On pose
![]() $f_{1,+}={\mathcal{Q}}(t_{1,+}^{\prime },t_{1,+}^{\prime \prime })^{\operatorname{Lie}}\circ \unicode[STIX]{x1D70C}_{N_{+}^{\prime }}\circ \unicode[STIX]{x1D704}_{N_{+}^{\prime },0}(\unicode[STIX]{x1D711}_{v_{+}^{\prime }})$
et
$f_{1,+}={\mathcal{Q}}(t_{1,+}^{\prime },t_{1,+}^{\prime \prime })^{\operatorname{Lie}}\circ \unicode[STIX]{x1D70C}_{N_{+}^{\prime }}\circ \unicode[STIX]{x1D704}_{N_{+}^{\prime },0}(\unicode[STIX]{x1D711}_{v_{+}^{\prime }})$
et
![]() $f_{2,+}={\mathcal{Q}}(t_{2,+}^{\prime },t_{2,+}^{\prime \prime })^{\operatorname{Lie}}\circ \unicode[STIX]{x1D70C}_{N_{+}^{\prime \prime }}\circ \unicode[STIX]{x1D704}_{N_{+}^{\prime \prime },0}(\unicode[STIX]{x1D711}_{v_{+}^{\prime \prime }})$
. Alors
$f_{2,+}={\mathcal{Q}}(t_{2,+}^{\prime },t_{2,+}^{\prime \prime })^{\operatorname{Lie}}\circ \unicode[STIX]{x1D70C}_{N_{+}^{\prime \prime }}\circ \unicode[STIX]{x1D704}_{N_{+}^{\prime \prime },0}(\unicode[STIX]{x1D711}_{v_{+}^{\prime \prime }})$
. Alors
En adaptant de façon similaire les notations et définitions, le lemme 2.2 fournit l’égalité
tandis que le lemme 2.3 fournit l’égalité
Posons
![]() $f_{1}[\mathbf{v}]=f_{1,+}\,\otimes \,f_{1,-}\,\otimes \,\otimes _{i\in I}f_{1,i}$
et
$f_{1}[\mathbf{v}]=f_{1,+}\,\otimes \,f_{1,-}\,\otimes \,\otimes _{i\in I}f_{1,i}$
et
Définissons de même
![]() $f_{2}[\mathbf{v}]$
et
$f_{2}[\mathbf{v}]$
et
![]() $S(X_{2},f_{2}[\mathbf{v}])$
. Alors l’expression (1) ci-dessus vaut
$S(X_{2},f_{2}[\mathbf{v}])$
. Alors l’expression (1) ci-dessus vaut
Définissons une nouvelle constante
![]() $C(r^{\prime },r^{\prime \prime },w^{\prime },w^{\prime \prime })$
par les égalités
$C(r^{\prime },r^{\prime \prime },w^{\prime },w^{\prime \prime })$
par les égalités
si
![]() $r^{\prime \prime }\leqslant r^{\prime }$
,
$r^{\prime \prime }\leqslant r^{\prime }$
,
si
![]() $r^{\prime }<r^{\prime \prime }$
,
$r^{\prime }<r^{\prime \prime }$
,
Montrons que
(4) l’expression (1) vaut
Supposons d’abord que
![]() $r^{\prime \prime }\leqslant r^{\prime }$
. Alors
$r^{\prime \prime }\leqslant r^{\prime }$
. Alors
![]() $r^{\prime \prime }\leqslant r_{+}^{\prime }$
et
$r^{\prime \prime }\leqslant r_{+}^{\prime }$
et
![]() $r^{\prime \prime }\leqslant r_{-}^{\prime }$
. En utilisant les définitions de 2.1 et 2.2, on obtient
$r^{\prime \prime }\leqslant r_{-}^{\prime }$
. En utilisant les définitions de 2.1 et 2.2, on obtient
 $$\begin{eqnarray}\displaystyle C_{+}(\mathbf{v})C_{-}(\mathbf{v}) & = & \displaystyle \operatorname{sgn}(-1)^{\frac{r_{+}^{\prime }+r^{\prime \prime }-1}{2}+\operatorname{val}_{F}(\unicode[STIX]{x1D702}_{+})}\operatorname{sgn}(\unicode[STIX]{x1D702}_{2,+}\unicode[STIX]{x1D71B}^{-\operatorname{val}_{F}(\unicode[STIX]{x1D702}_{2,+})})^{\operatorname{val}_{F}(\unicode[STIX]{x1D702}_{+})}\nonumber\\ \displaystyle & & \displaystyle \times \,\operatorname{sgn}(\unicode[STIX]{x1D702}_{2,-}\unicode[STIX]{x1D71B}^{-\operatorname{val}_{F}(\unicode[STIX]{x1D702}_{2,-})})^{\operatorname{val}_{F}(\unicode[STIX]{x1D702}_{-})}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle C_{+}(\mathbf{v})C_{-}(\mathbf{v}) & = & \displaystyle \operatorname{sgn}(-1)^{\frac{r_{+}^{\prime }+r^{\prime \prime }-1}{2}+\operatorname{val}_{F}(\unicode[STIX]{x1D702}_{+})}\operatorname{sgn}(\unicode[STIX]{x1D702}_{2,+}\unicode[STIX]{x1D71B}^{-\operatorname{val}_{F}(\unicode[STIX]{x1D702}_{2,+})})^{\operatorname{val}_{F}(\unicode[STIX]{x1D702}_{+})}\nonumber\\ \displaystyle & & \displaystyle \times \,\operatorname{sgn}(\unicode[STIX]{x1D702}_{2,-}\unicode[STIX]{x1D71B}^{-\operatorname{val}_{F}(\unicode[STIX]{x1D702}_{2,-})})^{\operatorname{val}_{F}(\unicode[STIX]{x1D702}_{-})}.\nonumber\end{eqnarray}$$
D’après 3.1(2) et l’hypothèse (1)(a) de 3.2 (qui est vérifiée),
![]() $\operatorname{val}_{F}(\unicode[STIX]{x1D702}_{+})=-\text{val}_{F}(\unicode[STIX]{x1D702}_{-})\equiv r^{\prime \prime }\,\,\text{mod}\,\,2\,\mathbb{Z}$
. D’après la même relation 3.1(2) appliquée aux données indexées par
$\operatorname{val}_{F}(\unicode[STIX]{x1D702}_{+})=-\text{val}_{F}(\unicode[STIX]{x1D702}_{-})\equiv r^{\prime \prime }\,\,\text{mod}\,\,2\,\mathbb{Z}$
. D’après la même relation 3.1(2) appliquée aux données indexées par
![]() $2$
, on a
$2$
, on a
![]() $\operatorname{val}_{F}(\unicode[STIX]{x1D702}_{2,+})+\operatorname{val}_{F}(\unicode[STIX]{x1D702}_{2,-})=0$
et
$\operatorname{val}_{F}(\unicode[STIX]{x1D702}_{2,+})+\operatorname{val}_{F}(\unicode[STIX]{x1D702}_{2,-})=0$
et
![]() $\operatorname{sgn}(\unicode[STIX]{x1D702}_{2,+}\unicode[STIX]{x1D702}_{2,-})=(-1)^{d_{2}}$
. On en déduit l’égalité
$\operatorname{sgn}(\unicode[STIX]{x1D702}_{2,+}\unicode[STIX]{x1D702}_{2,-})=(-1)^{d_{2}}$
. On en déduit l’égalité
![]() $C_{+}(\mathbf{v})C_{-}(\mathbf{v})=C(r^{\prime },r^{\prime \prime },w^{\prime },w^{\prime \prime })$
. Supposons maintenant que
$C_{+}(\mathbf{v})C_{-}(\mathbf{v})=C(r^{\prime },r^{\prime \prime },w^{\prime },w^{\prime \prime })$
. Supposons maintenant que
![]() $r^{\prime }\leqslant r^{\prime \prime }-2$
. Alors
$r^{\prime }\leqslant r^{\prime \prime }-2$
. Alors
![]() $r_{+}^{\prime }<r^{\prime \prime }$
et
$r_{+}^{\prime }<r^{\prime \prime }$
et
![]() $r_{-}^{\prime }<r^{\prime \prime }$
. On voit que
$r_{-}^{\prime }<r^{\prime \prime }$
. On voit que
![]() $C_{+}(\mathbf{v})C_{-}(\mathbf{v})$
est égal à
$C_{+}(\mathbf{v})C_{-}(\mathbf{v})$
est égal à
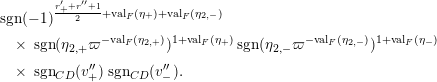 $$\begin{eqnarray}\displaystyle & & \displaystyle \operatorname{sgn}(-1)^{\frac{r_{+}^{\prime }+r^{\prime \prime }+1}{2}+\operatorname{val}_{F}(\unicode[STIX]{x1D702}_{+})+\operatorname{val}_{F}(\unicode[STIX]{x1D702}_{2,-})}\nonumber\\ \displaystyle & & \displaystyle \quad \times \,\operatorname{sgn}(\unicode[STIX]{x1D702}_{2,+}\unicode[STIX]{x1D71B}^{-\text{val}_{F}(\unicode[STIX]{x1D702}_{2,+})})^{1+\operatorname{val}_{F}(\unicode[STIX]{x1D702}_{+})}\operatorname{sgn}(\unicode[STIX]{x1D702}_{2,-}\unicode[STIX]{x1D71B}^{-\text{val}_{F}(\unicode[STIX]{x1D702}_{2,-})})^{1+\operatorname{val}_{F}(\unicode[STIX]{x1D702}_{-})}\nonumber\\ \displaystyle & & \displaystyle \quad \times \,\operatorname{sgn}_{CD}(v_{+}^{\prime \prime })\operatorname{sgn}_{CD}(v_{-}^{\prime \prime }).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \operatorname{sgn}(-1)^{\frac{r_{+}^{\prime }+r^{\prime \prime }+1}{2}+\operatorname{val}_{F}(\unicode[STIX]{x1D702}_{+})+\operatorname{val}_{F}(\unicode[STIX]{x1D702}_{2,-})}\nonumber\\ \displaystyle & & \displaystyle \quad \times \,\operatorname{sgn}(\unicode[STIX]{x1D702}_{2,+}\unicode[STIX]{x1D71B}^{-\text{val}_{F}(\unicode[STIX]{x1D702}_{2,+})})^{1+\operatorname{val}_{F}(\unicode[STIX]{x1D702}_{+})}\operatorname{sgn}(\unicode[STIX]{x1D702}_{2,-}\unicode[STIX]{x1D71B}^{-\text{val}_{F}(\unicode[STIX]{x1D702}_{2,-})})^{1+\operatorname{val}_{F}(\unicode[STIX]{x1D702}_{-})}\nonumber\\ \displaystyle & & \displaystyle \quad \times \,\operatorname{sgn}_{CD}(v_{+}^{\prime \prime })\operatorname{sgn}_{CD}(v_{-}^{\prime \prime }).\nonumber\end{eqnarray}$$
Comme ci-dessus, le produit des deuxième et troisième termes vaut
![]() $(-1)^{d_{2}(1+r^{\prime \prime })}$
. On a
$(-1)^{d_{2}(1+r^{\prime \prime })}$
. On a
 $$\begin{eqnarray}\displaystyle \operatorname{val}_{F}(\unicode[STIX]{x1D702}_{+})+\operatorname{val}_{F}(\unicode[STIX]{x1D702}_{2,-}) & = & \displaystyle -\text{val}_{F}(\unicode[STIX]{x1D702}_{-})+\operatorname{val}_{F}(\unicode[STIX]{x1D702}_{2,-})\nonumber\\ \displaystyle & = & \displaystyle -\text{val}_{F}(\unicode[STIX]{x1D702}_{1,-})\equiv \frac{r_{-}^{\prime }+r^{\prime \prime }}{2}\,\,\text{mod}\,\,2\,\mathbb{Z}\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \operatorname{val}_{F}(\unicode[STIX]{x1D702}_{+})+\operatorname{val}_{F}(\unicode[STIX]{x1D702}_{2,-}) & = & \displaystyle -\text{val}_{F}(\unicode[STIX]{x1D702}_{-})+\operatorname{val}_{F}(\unicode[STIX]{x1D702}_{2,-})\nonumber\\ \displaystyle & = & \displaystyle -\text{val}_{F}(\unicode[STIX]{x1D702}_{1,-})\equiv \frac{r_{-}^{\prime }+r^{\prime \prime }}{2}\,\,\text{mod}\,\,2\,\mathbb{Z}\nonumber\end{eqnarray}$$
d’après (2) ci-dessus. Puisque
![]() $r_{+}^{\prime }+r_{-}^{\prime }=2r^{\prime }+1$
, on voit que la puissance de
$r_{+}^{\prime }+r_{-}^{\prime }=2r^{\prime }+1$
, on voit que la puissance de
![]() $\operatorname{sgn}(-1)$
dans l’expression ci-dessus coïncide avec celle figurant dans
$\operatorname{sgn}(-1)$
dans l’expression ci-dessus coïncide avec celle figurant dans
![]() $C(r^{\prime },r^{\prime \prime },w^{\prime },w^{\prime \prime })$
. D’après la définition de
$C(r^{\prime },r^{\prime \prime },w^{\prime },w^{\prime \prime })$
. D’après la définition de
![]() $\mathbf{d}$
et le fait que
$\mathbf{d}$
et le fait que
![]() $\mathbf{v}\in {\mathcal{V}}(\mathbf{d})$
, on a l’égalité
$\mathbf{v}\in {\mathcal{V}}(\mathbf{d})$
, on a l’égalité
![]() $\operatorname{sgn}_{CD}(v_{+}^{\prime \prime })\operatorname{sgn}_{CD}(v_{-}^{\prime \prime })=\operatorname{sgn}_{CD}(w^{\prime \prime })\operatorname{sgn}(\unicode[STIX]{x1D702}_{2,+}\unicode[STIX]{x1D702}_{2,-})$
. Ce dernier facteur est égal à
$\operatorname{sgn}_{CD}(v_{+}^{\prime \prime })\operatorname{sgn}_{CD}(v_{-}^{\prime \prime })=\operatorname{sgn}_{CD}(w^{\prime \prime })\operatorname{sgn}(\unicode[STIX]{x1D702}_{2,+}\unicode[STIX]{x1D702}_{2,-})$
. Ce dernier facteur est égal à
![]() $(-1)^{d_{2}}$
comme on l’a déjà dit. En rassemblant ces calculs, on obtient de nouveau l’égalité
$(-1)^{d_{2}}$
comme on l’a déjà dit. En rassemblant ces calculs, on obtient de nouveau l’égalité
![]() $C_{+}(\mathbf{v})C_{-}(\mathbf{v})=C(r^{\prime },r^{\prime \prime },w^{\prime },w^{\prime \prime })$
. Supposons maintenant que
$C_{+}(\mathbf{v})C_{-}(\mathbf{v})=C(r^{\prime },r^{\prime \prime },w^{\prime },w^{\prime \prime })$
. Supposons maintenant que
![]() $r^{\prime }=r^{\prime \prime }-1$
. Alors
$r^{\prime }=r^{\prime \prime }-1$
. Alors
![]() $r_{+}^{\prime }=r^{\prime }<r^{\prime \prime }$
mais
$r_{+}^{\prime }=r^{\prime }<r^{\prime \prime }$
mais
![]() $r_{-}^{\prime }=r^{\prime }+1=r^{\prime \prime }$
. Comme dans le cas
$r_{-}^{\prime }=r^{\prime }+1=r^{\prime \prime }$
. Comme dans le cas
![]() $r^{\prime }\leqslant r^{\prime \prime }-2$
, on obtiendrait l’égalité voulue si
$r^{\prime }\leqslant r^{\prime \prime }-2$
, on obtiendrait l’égalité voulue si
![]() $C_{-}(\mathbf{v})$
était définie par les formules du cas
$C_{-}(\mathbf{v})$
était définie par les formules du cas
![]() $r_{-}^{\prime }<r^{\prime \prime }$
, et non par celles de notre cas
$r_{-}^{\prime }<r^{\prime \prime }$
, et non par celles de notre cas
![]() $r_{-}^{\prime }\geqslant r^{\prime \prime }$
. Le rapport entre les deux formules est
$r_{-}^{\prime }\geqslant r^{\prime \prime }$
. Le rapport entre les deux formules est
Si cette expression vaut
![]() $1$
, on a fini. Supposons qu’elle vaille
$1$
, on a fini. Supposons qu’elle vaille
![]() $-1$
. Puisque
$-1$
. Puisque
![]() $r_{-}^{\prime }=r^{\prime \prime }$
, l’hypothèse (2) plus haut implique que
$r_{-}^{\prime }=r^{\prime \prime }$
, l’hypothèse (2) plus haut implique que
![]() $\operatorname{val}_{F}(\unicode[STIX]{x1D702}_{2,-})$
est paire, ce qui fait disparaître le premier terme de notre expression. On a aussi
$\operatorname{val}_{F}(\unicode[STIX]{x1D702}_{2,-})$
est paire, ce qui fait disparaître le premier terme de notre expression. On a aussi
![]() $r_{2,-}^{\prime }=r_{2,-}^{\prime \prime }=\frac{|r_{-}^{\prime }-r^{\prime \prime }|}{2}=0$
. La remarque de 2.2 entraîne que, sous notre hypothèse selon laquelle (5) vaut
$r_{2,-}^{\prime }=r_{2,-}^{\prime \prime }=\frac{|r_{-}^{\prime }-r^{\prime \prime }|}{2}=0$
. La remarque de 2.2 entraîne que, sous notre hypothèse selon laquelle (5) vaut
![]() $-1$
,
$-1$
,
![]() $f_{2,-}$
est nulle, donc
$f_{2,-}$
est nulle, donc
![]() $f_{2}[\mathbf{v}]$
aussi. Mais alors
$f_{2}[\mathbf{v}]$
aussi. Mais alors
![]() $S(X_{2},f_{2}[\mathbf{v}])=0$
et la constante n’a plus d’importance. Cela prouve (4).
$S(X_{2},f_{2}[\mathbf{v}])=0$
et la constante n’a plus d’importance. Cela prouve (4).
L’égalité 3.3(2) devient
 $$\begin{eqnarray}\displaystyle J^{\operatorname{endo}}(x_{1},x_{2},f) & = & \displaystyle c(r^{\prime },r^{\prime \prime })c(r^{\prime },r^{\prime \prime },w^{\prime },w^{\prime \prime })C(r^{\prime },r^{\prime \prime },w^{\prime },w^{\prime \prime })(-1)^{d_{2}r^{\prime \prime }}\nonumber\\ \displaystyle & & \displaystyle \times \,\mathop{\sum }_{\mathbf{v}\in {\mathcal{V}}(\mathbf{d})}S(X_{1},f_{1}[\mathbf{v}])S(X_{2},f_{2}[\mathbf{v}]).\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle J^{\operatorname{endo}}(x_{1},x_{2},f) & = & \displaystyle c(r^{\prime },r^{\prime \prime })c(r^{\prime },r^{\prime \prime },w^{\prime },w^{\prime \prime })C(r^{\prime },r^{\prime \prime },w^{\prime },w^{\prime \prime })(-1)^{d_{2}r^{\prime \prime }}\nonumber\\ \displaystyle & & \displaystyle \times \,\mathop{\sum }_{\mathbf{v}\in {\mathcal{V}}(\mathbf{d})}S(X_{1},f_{1}[\mathbf{v}])S(X_{2},f_{2}[\mathbf{v}]).\end{eqnarray}$$
Comme en 1.2, on définit des entiers
![]() $r_{1}^{\prime },r_{1}^{\prime \prime },r_{2}^{\prime },r_{2}^{\prime \prime }$
et les fonctions
$r_{1}^{\prime },r_{1}^{\prime \prime },r_{2}^{\prime },r_{2}^{\prime \prime }$
et les fonctions
![]() $f_{1}=\unicode[STIX]{x1D6F9}\circ k\circ \unicode[STIX]{x1D70C}\unicode[STIX]{x1D704}(\unicode[STIX]{x1D711}_{w^{\prime }})$
et
$f_{1}=\unicode[STIX]{x1D6F9}\circ k\circ \unicode[STIX]{x1D70C}\unicode[STIX]{x1D704}(\unicode[STIX]{x1D711}_{w^{\prime }})$
et
![]() $f_{2}=\unicode[STIX]{x1D6F9}\circ k\circ \unicode[STIX]{x1D70C}\unicode[STIX]{x1D704}(\unicode[STIX]{x1D711}_{w^{\prime \prime }})$
. Les intégrales orbitales stables
$f_{2}=\unicode[STIX]{x1D6F9}\circ k\circ \unicode[STIX]{x1D70C}\unicode[STIX]{x1D704}(\unicode[STIX]{x1D711}_{w^{\prime \prime }})$
. Les intégrales orbitales stables
![]() $S(x_{1},f_{1})$
et
$S(x_{1},f_{1})$
et
![]() $S(x_{2},f_{2})$
sont des cas particuliers d’intégrales endoscopiques
$S(x_{2},f_{2})$
sont des cas particuliers d’intégrales endoscopiques
![]() $J^{\operatorname{endo}}(x_{1},x_{2},f)$
. Elles sont donc nulles si les analogues des hypothèses (2) et (3) ne sont pas vérifiées. Sinon, elles sont données par des formules similaires à (6). Dans toutes ces formules, les termes indexés par l’indice
$J^{\operatorname{endo}}(x_{1},x_{2},f)$
. Elles sont donc nulles si les analogues des hypothèses (2) et (3) ne sont pas vérifiées. Sinon, elles sont données par des formules similaires à (6). Dans toutes ces formules, les termes indexés par l’indice
![]() $2$
disparaissent, ainsi que ceux faisant intervenir
$2$
disparaissent, ainsi que ceux faisant intervenir
![]() $N^{\prime \prime }$
et
$N^{\prime \prime }$
et
![]() $w^{\prime \prime }$
. D’autre part, l’analogue de l’entier
$w^{\prime \prime }$
. D’autre part, l’analogue de l’entier
![]() $b\in \{0,1\}$
est toujours
$b\in \{0,1\}$
est toujours
![]() $0$
. En effet, d’après les définitions, on a
$0$
. En effet, d’après les définitions, on a
![]() $r_{1}^{\prime \prime },r_{2}^{\prime \prime }\geqslant 0$
et si, par exemple,
$r_{1}^{\prime \prime },r_{2}^{\prime \prime }\geqslant 0$
et si, par exemple,
![]() $r_{1}^{\prime \prime }=0$
, on a aussi
$r_{1}^{\prime \prime }=0$
, on a aussi
![]() $r_{1}^{\prime }=0$
donc
$r_{1}^{\prime }=0$
donc
![]() $r_{1}^{\prime }$
pair. On voit que l’analogue de (2) pour
$r_{1}^{\prime }$
pair. On voit que l’analogue de (2) pour
![]() $S(x_{1},f_{1})$
est
$S(x_{1},f_{1})$
est
![]() $\operatorname{val}_{F}(\unicode[STIX]{x1D702}_{1,-})\equiv \frac{r_{1,-}^{\prime }+r_{1}^{\prime \prime }}{2}\,\,\text{mod}\,\,2\,\mathbb{Z}$
, tandis que l’analogue pour
$\operatorname{val}_{F}(\unicode[STIX]{x1D702}_{1,-})\equiv \frac{r_{1,-}^{\prime }+r_{1}^{\prime \prime }}{2}\,\,\text{mod}\,\,2\,\mathbb{Z}$
, tandis que l’analogue pour
![]() $S(x_{2},f_{2})$
est
$S(x_{2},f_{2})$
est
![]() $\operatorname{val}_{F}(\unicode[STIX]{x1D702}_{2,-})\equiv \frac{r_{2,-}^{\prime }+r_{2}^{\prime \prime }}{2}\,\,\text{mod}\,\,2\,\mathbb{Z}$
. D’après la relation (3) du paragraphe 4 ci-après,
$\operatorname{val}_{F}(\unicode[STIX]{x1D702}_{2,-})\equiv \frac{r_{2,-}^{\prime }+r_{2}^{\prime \prime }}{2}\,\,\text{mod}\,\,2\,\mathbb{Z}$
. D’après la relation (3) du paragraphe 4 ci-après,
![]() $r_{1,-}^{\prime }+r_{1}^{\prime \prime }=r_{-}^{\prime }+r^{\prime \prime }$
,
$r_{1,-}^{\prime }+r_{1}^{\prime \prime }=r_{-}^{\prime }+r^{\prime \prime }$
,
![]() $r_{2,-}^{\prime }+r_{2}^{\prime \prime }=|r_{-}^{\prime }-r^{\prime \prime }|$
. Il en résulte que la conjonction des deux analogues de (2) est équivalente à cette relation (2) elle-même. L’analogue de (3) ci-dessus pour
$r_{2,-}^{\prime }+r_{2}^{\prime \prime }=|r_{-}^{\prime }-r^{\prime \prime }|$
. Il en résulte que la conjonction des deux analogues de (2) est équivalente à cette relation (2) elle-même. L’analogue de (3) ci-dessus pour
![]() $S(x_{1},f_{1})$
est
$S(x_{1},f_{1})$
est
tandis que l’analogue pour
![]() $S(x_{2},f_{2})$
est
$S(x_{2},f_{2})$
est
De nouveau, le calcul montre que la conjonction de ces conditions est équivalente à la relation (3) elle-même. Cela démontre que, si (2) et (3) ne sont pas vérifiées,
![]() $S(x_{1},f_{1})S(x_{2},f_{2})=0$
. Puisque l’on a déjà vu que
$S(x_{1},f_{1})S(x_{2},f_{2})=0$
. Puisque l’on a déjà vu que
![]() $J^{\operatorname{endo}}(x_{1},x_{2},f)=0$
, on obtient
$J^{\operatorname{endo}}(x_{1},x_{2},f)=0$
, on obtient
![]() $J^{\operatorname{endo}}(x_{1},x_{2},f)=S(x_{1},f_{1})S(x_{2},f_{2})$
dans ce cas.
$J^{\operatorname{endo}}(x_{1},x_{2},f)=S(x_{1},f_{1})S(x_{2},f_{2})$
dans ce cas.
On suppose maintenant vérifiées nos hypothèses (2) et (3). De même que l’on a déterminé un unique
![]() $\mathbf{d}\in D$
, on détermine un unique
$\mathbf{d}\in D$
, on détermine un unique
![]() $\mathbf{d}_{1}$
relatif à
$\mathbf{d}_{1}$
relatif à
![]() $S(x_{1},f_{1})$
et un unique
$S(x_{1},f_{1})$
et un unique
![]() $\mathbf{d}_{2}$
relatif à
$\mathbf{d}_{2}$
relatif à
![]() $S(x_{2},f_{2})$
. Écrivons
$S(x_{2},f_{2})$
. Écrivons
![]() $\mathbf{d}=(N_{+}^{\prime },N_{-}^{\prime },N_{+}^{\prime \prime },N_{-}^{\prime \prime },(d_{i}^{\prime },d_{i}^{\prime \prime })_{i\in I})$
. Tous ces entiers sont déterminés par la relation 3.3(4). De même,
$\mathbf{d}=(N_{+}^{\prime },N_{-}^{\prime },N_{+}^{\prime \prime },N_{-}^{\prime \prime },(d_{i}^{\prime },d_{i}^{\prime \prime })_{i\in I})$
. Tous ces entiers sont déterminés par la relation 3.3(4). De même,
![]() $\mathbf{d}_{1}$
et
$\mathbf{d}_{1}$
et
![]() $\mathbf{d}_{2}$
sont déterminés par les analogues de cette relation. Par les mêmes calculs que ci-dessus, on voit que
$\mathbf{d}_{2}$
sont déterminés par les analogues de cette relation. Par les mêmes calculs que ci-dessus, on voit que
![]() $\mathbf{d}_{1}=(N_{+}^{\prime },N_{-}^{\prime },0,0,(d_{i}^{\prime },0)_{i\in I})$
tandis que
$\mathbf{d}_{1}=(N_{+}^{\prime },N_{-}^{\prime },0,0,(d_{i}^{\prime },0)_{i\in I})$
tandis que
![]() $\mathbf{d}_{2}=(N_{+}^{\prime \prime },N_{-}^{\prime \prime },0,0,(d_{i}^{\prime \prime },0)_{i\in I})$
. On en déduit que
$\mathbf{d}_{2}=(N_{+}^{\prime \prime },N_{-}^{\prime \prime },0,0,(d_{i}^{\prime \prime },0)_{i\in I})$
. On en déduit que
![]() ${\mathcal{V}}^{\prime }(\mathbf{d})\simeq {\mathcal{V}}(\mathbf{d}_{1})$
et
${\mathcal{V}}^{\prime }(\mathbf{d})\simeq {\mathcal{V}}(\mathbf{d}_{1})$
et
![]() ${\mathcal{V}}^{\prime \prime }(\mathbf{d})\simeq {\mathcal{V}}(\mathbf{d}_{2})$
, d’où
${\mathcal{V}}^{\prime \prime }(\mathbf{d})\simeq {\mathcal{V}}(\mathbf{d}_{2})$
, d’où
![]() ${\mathcal{V}}(\mathbf{d})\simeq {\mathcal{V}}(\mathbf{d}_{1})\times {\mathcal{V}}(\mathbf{d}_{2})$
. On identifie ces deux ensembles. À l’aide de
${\mathcal{V}}(\mathbf{d})\simeq {\mathcal{V}}(\mathbf{d}_{1})\times {\mathcal{V}}(\mathbf{d}_{2})$
. On identifie ces deux ensembles. À l’aide de
![]() $r^{\prime },r^{\prime \prime }$
,
$r^{\prime },r^{\prime \prime }$
,
![]() $\mathbf{d}$
et d’un élément
$\mathbf{d}$
et d’un élément
![]() $\mathbf{v}\in {\mathcal{V}}(\mathbf{d})$
, on a défini une fonction
$\mathbf{v}\in {\mathcal{V}}(\mathbf{d})$
, on a défini une fonction
![]() $f_{1}[\mathbf{v}]$
. Pour
$f_{1}[\mathbf{v}]$
. Pour
![]() $j=1,2$
, à l’aide de
$j=1,2$
, à l’aide de
![]() $r_{j}^{\prime },r_{j}^{\prime \prime }$
,
$r_{j}^{\prime },r_{j}^{\prime \prime }$
,
![]() $\mathbf{d}_{j}$
et d’un élément
$\mathbf{d}_{j}$
et d’un élément
![]() $\mathbf{v}_{j}\in {\mathcal{V}}(\mathbf{d}_{j})$
, on définit de même une fonction
$\mathbf{v}_{j}\in {\mathcal{V}}(\mathbf{d}_{j})$
, on définit de même une fonction
![]() $f_{j}[\mathbf{v}_{j}]$
. Les analogues de l’égalité (6) sont
$f_{j}[\mathbf{v}_{j}]$
. Les analogues de l’égalité (6) sont
où l’on a adapté de façon évidente la notation des constantes.
Soit
![]() $\mathbf{v}=(\mathbf{v}_{1},\mathbf{v}_{2})\in {\mathcal{V}}(\mathbf{d})$
. Montrons que
$\mathbf{v}=(\mathbf{v}_{1},\mathbf{v}_{2})\in {\mathcal{V}}(\mathbf{d})$
. Montrons que
(8)
![]() $f_{1}[\mathbf{v}]=f_{1}[\mathbf{v}_{1}]$
,
$f_{1}[\mathbf{v}]=f_{1}[\mathbf{v}_{1}]$
,
![]() $f_{2}[\mathbf{v}]=f_{2}[\mathbf{v}_{2}]$
.
$f_{2}[\mathbf{v}]=f_{2}[\mathbf{v}_{2}]$
.
On traite le cas de l’indice
![]() $1$
. D’après la définition donnée plus haut,
$1$
. D’après la définition donnée plus haut,
![]() $f_{1}[\mathbf{v}]=f_{1,+}\,\otimes \,f_{1,-}\,\otimes \,\otimes _{i\in I}f_{1,i}$
, avec par exemple
$f_{1}[\mathbf{v}]=f_{1,+}\,\otimes \,f_{1,-}\,\otimes \,\otimes _{i\in I}f_{1,i}$
, avec par exemple
![]() $f_{1,+}={\mathcal{Q}}(t_{1,+}^{\prime },t_{1,+}^{\prime \prime })^{\operatorname{Lie}}\circ \unicode[STIX]{x1D70C}_{N_{+}^{\prime }}\circ \unicode[STIX]{x1D704}_{N_{+}^{\prime },0}(\unicode[STIX]{x1D711}_{v_{+}^{\prime }})$
. Quand l’on remplace
$f_{1,+}={\mathcal{Q}}(t_{1,+}^{\prime },t_{1,+}^{\prime \prime })^{\operatorname{Lie}}\circ \unicode[STIX]{x1D70C}_{N_{+}^{\prime }}\circ \unicode[STIX]{x1D704}_{N_{+}^{\prime },0}(\unicode[STIX]{x1D711}_{v_{+}^{\prime }})$
. Quand l’on remplace
![]() $r^{\prime }$
,
$r^{\prime }$
,
![]() $r^{\prime \prime }$
,
$r^{\prime \prime }$
,
![]() $\mathbf{d}$
et
$\mathbf{d}$
et
![]() $\mathbf{v}$
par
$\mathbf{v}$
par
![]() $r_{1}^{\prime }$
,
$r_{1}^{\prime }$
,
![]() $r_{1}^{\prime \prime }$
,
$r_{1}^{\prime \prime }$
,
![]() $\mathbf{d}_{1}$
et
$\mathbf{d}_{1}$
et
![]() $\mathbf{v}_{1}$
, les termes
$\mathbf{v}_{1}$
, les termes
![]() $N_{+}^{\prime }$
et
$N_{+}^{\prime }$
et
![]() $v_{+}^{\prime }$
ne changent pas. Les entiers
$v_{+}^{\prime }$
ne changent pas. Les entiers
![]() $t_{1,+}^{\prime }$
et
$t_{1,+}^{\prime }$
et
![]() $t_{1,+}^{\prime \prime }$
sont définis par
$t_{1,+}^{\prime \prime }$
sont définis par
![]() $\{t_{1,+}^{\prime },t_{1,+}^{\prime \prime }\}=\{\frac{r_{+}^{\prime }+r^{\prime \prime }+1}{2},\frac{r_{+}^{\prime }+r^{\prime \prime }-1}{2}\}$
et
$\{t_{1,+}^{\prime },t_{1,+}^{\prime \prime }\}=\{\frac{r_{+}^{\prime }+r^{\prime \prime }+1}{2},\frac{r_{+}^{\prime }+r^{\prime \prime }-1}{2}\}$
et
![]() $t_{1,+}^{\prime }\equiv 1+\operatorname{val}_{F}(\unicode[STIX]{x1D702}_{1,+})\,\,\text{mod}\,\,2\,\mathbb{Z}$
. La relation (3) du paragraphe 4 ci-après montre que l’ensemble
$t_{1,+}^{\prime }\equiv 1+\operatorname{val}_{F}(\unicode[STIX]{x1D702}_{1,+})\,\,\text{mod}\,\,2\,\mathbb{Z}$
. La relation (3) du paragraphe 4 ci-après montre que l’ensemble
![]() $\{\frac{r_{+}^{\prime }+r^{\prime \prime }+1}{2},\frac{r_{+}^{\prime }+r^{\prime \prime }-1}{2}\}$
ne change pas quand l’on remplace
$\{\frac{r_{+}^{\prime }+r^{\prime \prime }+1}{2},\frac{r_{+}^{\prime }+r^{\prime \prime }-1}{2}\}$
ne change pas quand l’on remplace
![]() $r^{\prime },r^{\prime \prime }$
par
$r^{\prime },r^{\prime \prime }$
par
![]() $r_{1}^{\prime },r_{1}^{\prime \prime }$
. La congruence exigée non plus. Donc
$r_{1}^{\prime },r_{1}^{\prime \prime }$
. La congruence exigée non plus. Donc
![]() $t_{1,+}^{\prime }$
et
$t_{1,+}^{\prime }$
et
![]() $t_{1,+}^{\prime \prime }$
ne changent pas et
$t_{1,+}^{\prime \prime }$
ne changent pas et
![]() $f_{1,+}$
non plus. Un calcul analogue s’applique aux composantes
$f_{1,+}$
non plus. Un calcul analogue s’applique aux composantes
![]() $f_{1,-}$
et
$f_{1,-}$
et
![]() $f_{1,i}$
pour
$f_{1,i}$
pour
![]() $i\in I$
. Cela prouve (8).
$i\in I$
. Cela prouve (8).
De (6),
![]() $(7)_{1}$
et
$(7)_{1}$
et
![]() $(7)_{2}$
se déduit l’égalité
$(7)_{2}$
se déduit l’égalité
où
 $$\begin{eqnarray}\displaystyle C & = & \displaystyle c(r^{\prime },r^{\prime \prime })c(r^{\prime },r^{\prime \prime },w^{\prime },w^{\prime \prime })C(r^{\prime },r^{\prime \prime },w^{\prime },w^{\prime \prime })(-1)^{d_{2}r^{\prime \prime }}\nonumber\\ \displaystyle & & \displaystyle \times \,c(r_{1}^{\prime },r_{1}^{\prime \prime })c(r_{1}^{\prime },r_{1}^{\prime \prime },w^{\prime })C(r_{1}^{\prime },r_{1}^{\prime \prime },w^{\prime })\nonumber\\ \displaystyle & & \displaystyle \times \,c(r_{2}^{\prime },r_{2}^{\prime \prime })c(r_{2}^{\prime },r_{2}^{\prime \prime },w^{\prime \prime })C(r_{2}^{\prime },r_{2}^{\prime \prime },w^{\prime \prime }).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle C & = & \displaystyle c(r^{\prime },r^{\prime \prime })c(r^{\prime },r^{\prime \prime },w^{\prime },w^{\prime \prime })C(r^{\prime },r^{\prime \prime },w^{\prime },w^{\prime \prime })(-1)^{d_{2}r^{\prime \prime }}\nonumber\\ \displaystyle & & \displaystyle \times \,c(r_{1}^{\prime },r_{1}^{\prime \prime })c(r_{1}^{\prime },r_{1}^{\prime \prime },w^{\prime })C(r_{1}^{\prime },r_{1}^{\prime \prime },w^{\prime })\nonumber\\ \displaystyle & & \displaystyle \times \,c(r_{2}^{\prime },r_{2}^{\prime \prime })c(r_{2}^{\prime },r_{2}^{\prime \prime },w^{\prime \prime })C(r_{2}^{\prime },r_{2}^{\prime \prime },w^{\prime \prime }).\nonumber\end{eqnarray}$$
Remarquons que l’on n’a pas besoin d’inverser les coefficients de
![]() $(7)_{1}$
et
$(7)_{1}$
et
![]() $(7)_{2}$
: ce sont tous des signes. On a l’égalité
$(7)_{2}$
: ce sont tous des signes. On a l’égalité
(9)
![]() $C=1$
.
$C=1$
.
En reprenant les définitions des diverses constantes, on obtient l’égalité
où
![]() $U$
est défini au paragraphe 4 ci-après. Les autres termes sont les analogues relatifs aux données indexées par
$U$
est défini au paragraphe 4 ci-après. Les autres termes sont les analogues relatifs aux données indexées par
![]() $1$
et
$1$
et
![]() $2$
. Évidemment,
$2$
. Évidemment,
![]() $n=n_{1}+n_{2}$
et l’égalité
$n=n_{1}+n_{2}$
et l’égalité
![]() $C=1$
résulte de l’égalité
$C=1$
résulte de l’égalité
![]() $U=U_{1}U_{2}$
, cf. 4(4) ci-dessous.
$U=U_{1}U_{2}$
, cf. 4(4) ci-dessous.
À l’aide de (9), on obtient
![]() $J^{\operatorname{endo}}(x_{1},x_{2},f)=S(x_{1},f_{1})S(x_{2},f_{2})$
. Cette égalité est donc vérifiée avec ou sans les hypothèses (2) et (3) et elle l’est pour tous
$J^{\operatorname{endo}}(x_{1},x_{2},f)=S(x_{1},f_{1})S(x_{2},f_{2})$
. Cette égalité est donc vérifiée avec ou sans les hypothèses (2) et (3) et elle l’est pour tous
![]() $x_{1},x_{2}$
. Donc
$x_{1},x_{2}$
. Donc
![]() $f_{1}\,\otimes \,f_{2}$
est le transfert de
$f_{1}\,\otimes \,f_{2}$
est le transfert de
![]() $f$
. Cela démontre le (i) de la proposition 1.2 (sous l’hypothèse
$f$
. Cela démontre le (i) de la proposition 1.2 (sous l’hypothèse
![]() $b=0$
) pour les fonctions
$b=0$
) pour les fonctions
![]() $\unicode[STIX]{x1D711}^{\prime }=\unicode[STIX]{x1D711}_{w^{\prime }}$
et
$\unicode[STIX]{x1D711}^{\prime }=\unicode[STIX]{x1D711}_{w^{\prime }}$
et
![]() $\unicode[STIX]{x1D711}^{\prime \prime }=\unicode[STIX]{x1D711}_{w^{\prime \prime }}$
. Comme dans le paragraphe précédent, cela entraîne la même assertion pour toutes fonctions cuspidales
$\unicode[STIX]{x1D711}^{\prime \prime }=\unicode[STIX]{x1D711}_{w^{\prime \prime }}$
. Comme dans le paragraphe précédent, cela entraîne la même assertion pour toutes fonctions cuspidales
![]() $\unicode[STIX]{x1D711}^{\prime }$
et
$\unicode[STIX]{x1D711}^{\prime }$
et
![]() $\unicode[STIX]{x1D711}^{\prime \prime }$
.
$\unicode[STIX]{x1D711}^{\prime \prime }$
.
On a supposé que
![]() $b=0$
. Supposons maintenant que
$b=0$
. Supposons maintenant que
![]() $b=1$
. Comme on l’a dit en 3.3, la somme en
$b=1$
. Comme on l’a dit en 3.3, la somme en
![]() $X$
de 3.3(2) est alors égale à
$X$
de 3.3(2) est alors égale à
Le calcul se poursuit comme ci-dessus en permutant les rôles des indices
![]() $1$
et
$1$
et
![]() $2$
, en permutant
$2$
, en permutant
![]() $N^{\prime }$
et
$N^{\prime }$
et
![]() $N^{\prime \prime }$
, et en tenant compte de l’égalité
$N^{\prime \prime }$
, et en tenant compte de l’égalité
![]() $|r^{\prime \prime }|=-r^{\prime \prime }$
. Le résultat est le même, on laisse les détails au lecteur. Cela achève de prouver la proposition 1.2.◻
$|r^{\prime \prime }|=-r^{\prime \prime }$
. Le résultat est le même, on laisse les détails au lecteur. Cela achève de prouver la proposition 1.2.◻
4 Annexe
On rassemble ici quelques calculs élémentaires utilisés dans l’article. Soit
![]() $r^{\prime }\in \mathbb{N}$
et
$r^{\prime }\in \mathbb{N}$
et
![]() $r^{\prime \prime }\in \mathbb{Z}$
. On pose
$r^{\prime \prime }\in \mathbb{Z}$
. On pose
 $$\begin{eqnarray}\displaystyle r_{1}^{\prime } & = & \displaystyle \sup \biggl(\biggl[\frac{r^{\prime }+r^{\prime \prime }}{2}\biggr],-\biggl[\frac{r^{\prime }+r^{\prime \prime }}{2}\biggr]-1\biggr),\qquad r_{1}^{\prime \prime }=\biggl|\biggl[\frac{r^{\prime }+r^{\prime \prime }+1}{2}\biggr]\biggr|,\nonumber\\ \displaystyle r_{2}^{\prime } & = & \displaystyle \sup \biggl(\biggl[\frac{r^{\prime }-r^{\prime \prime }}{2}\biggr],-\biggl[\frac{r^{\prime }-r^{\prime \prime }}{2}\biggr]-1\biggr),\qquad r_{2}^{\prime \prime }=\biggl|\biggl[\frac{r^{\prime }-r^{\prime \prime }+1}{2}\biggr]\biggr|.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle r_{1}^{\prime } & = & \displaystyle \sup \biggl(\biggl[\frac{r^{\prime }+r^{\prime \prime }}{2}\biggr],-\biggl[\frac{r^{\prime }+r^{\prime \prime }}{2}\biggr]-1\biggr),\qquad r_{1}^{\prime \prime }=\biggl|\biggl[\frac{r^{\prime }+r^{\prime \prime }+1}{2}\biggr]\biggr|,\nonumber\\ \displaystyle r_{2}^{\prime } & = & \displaystyle \sup \biggl(\biggl[\frac{r^{\prime }-r^{\prime \prime }}{2}\biggr],-\biggl[\frac{r^{\prime }-r^{\prime \prime }}{2}\biggr]-1\biggr),\qquad r_{2}^{\prime \prime }=\biggl|\biggl[\frac{r^{\prime }-r^{\prime \prime }+1}{2}\biggr]\biggr|.\nonumber\end{eqnarray}$$
Remarquons que, si l’on change
![]() $r^{\prime \prime }$
en
$r^{\prime \prime }$
en
![]() $-r^{\prime \prime }$
, on échange les couples
$-r^{\prime \prime }$
, on échange les couples
![]() $(r_{1}^{\prime },r_{1}^{\prime \prime })$
et
$(r_{1}^{\prime },r_{1}^{\prime \prime })$
et
![]() $(r_{2}^{\prime },r_{2}^{\prime \prime })$
.
$(r_{2}^{\prime },r_{2}^{\prime \prime })$
.
(1) On a
![]() $r_{1}^{\prime \prime }+r_{2}^{\prime \prime }\equiv r^{\prime \prime }\,\,\text{mod}\,\,2\,\mathbb{Z}$
.
$r_{1}^{\prime \prime }+r_{2}^{\prime \prime }\equiv r^{\prime \prime }\,\,\text{mod}\,\,2\,\mathbb{Z}$
.
Preuve.
Puisque
![]() $m\equiv -m\,\,\text{mod}\,\,2\,\mathbb{Z}$
pour tout
$m\equiv -m\,\,\text{mod}\,\,2\,\mathbb{Z}$
pour tout
![]() $m\in \mathbb{Z}$
, on peut remplacer
$m\in \mathbb{Z}$
, on peut remplacer
![]() $r_{1}^{\prime \prime }$
par
$r_{1}^{\prime \prime }$
par
![]() $[\frac{r^{\prime }+r^{\prime \prime }+1}{2}]$
et
$[\frac{r^{\prime }+r^{\prime \prime }+1}{2}]$
et
![]() $r_{2}^{\prime \prime }$
par
$r_{2}^{\prime \prime }$
par
![]() $[\frac{r^{\prime }-r^{\prime \prime }+1}{2}]$
. On a
$[\frac{r^{\prime }-r^{\prime \prime }+1}{2}]$
. On a
![]() $[\frac{r^{\prime }-r^{\prime \prime }+1}{2}]=[\frac{r^{\prime }+r^{\prime \prime }+1}{2}-r^{\prime \prime }]=[\frac{r^{\prime }+r^{\prime \prime }+1}{2}]-r^{\prime \prime }$
, d’où (1).◻
$[\frac{r^{\prime }-r^{\prime \prime }+1}{2}]=[\frac{r^{\prime }+r^{\prime \prime }+1}{2}-r^{\prime \prime }]=[\frac{r^{\prime }+r^{\prime \prime }+1}{2}]-r^{\prime \prime }$
, d’où (1).◻
Pour faciliter les calculs qui suivent, on pose
![]() $a=0$
si
$a=0$
si
![]() $r^{\prime }+r^{\prime \prime }$
est pair et
$r^{\prime }+r^{\prime \prime }$
est pair et
![]() $a=1$
si
$a=1$
si
![]() $r^{\prime }+r^{\prime \prime }$
est impair,
$r^{\prime }+r^{\prime \prime }$
est impair,
![]() $A=0$
si
$A=0$
si
![]() $|r^{\prime \prime }|\leqslant r^{\prime }$
et
$|r^{\prime \prime }|\leqslant r^{\prime }$
et
![]() $A=1$
si
$A=1$
si
![]() $r^{\prime }<|r^{\prime \prime }|$
.
$r^{\prime }<|r^{\prime \prime }|$
.
(2) On a les égalités
 $$\begin{eqnarray}\displaystyle r_{1}^{\prime 2}+r_{1}^{\prime }+r_{1}^{\prime \prime 2} & = & \displaystyle \frac{(r^{\prime }+r^{\prime \prime })^{2}+(r^{\prime }+r^{\prime \prime }+1)^{2}-1}{4},\nonumber\\ \displaystyle r_{2}^{\prime 2}+r_{2}^{\prime }+r_{2}^{\prime \prime 2} & = & \displaystyle \frac{(r^{\prime }-r^{\prime \prime })^{2}+(r^{\prime }-r^{\prime \prime }+1)^{2}-1}{4}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle r_{1}^{\prime 2}+r_{1}^{\prime }+r_{1}^{\prime \prime 2} & = & \displaystyle \frac{(r^{\prime }+r^{\prime \prime })^{2}+(r^{\prime }+r^{\prime \prime }+1)^{2}-1}{4},\nonumber\\ \displaystyle r_{2}^{\prime 2}+r_{2}^{\prime }+r_{2}^{\prime \prime 2} & = & \displaystyle \frac{(r^{\prime }-r^{\prime \prime })^{2}+(r^{\prime }-r^{\prime \prime }+1)^{2}-1}{4}.\nonumber\end{eqnarray}$$
Preuve.
Pour
![]() $m\in \mathbb{Z}$
,
$m\in \mathbb{Z}$
,
![]() $m^{2}+m$
est invariant par la transformation
$m^{2}+m$
est invariant par la transformation
![]() $m\mapsto -m-1$
et
$m\mapsto -m-1$
et
![]() $m^{2}$
est invariant par
$m^{2}$
est invariant par
![]() $m\mapsto -m$
. On peut donc remplacer
$m\mapsto -m$
. On peut donc remplacer
![]() $r_{1}^{\prime }$
par
$r_{1}^{\prime }$
par
![]() $x^{\prime }=[\frac{r^{\prime }+r^{\prime \prime }}{2}]$
et
$x^{\prime }=[\frac{r^{\prime }+r^{\prime \prime }}{2}]$
et
![]() $r_{1}^{\prime \prime }$
par
$r_{1}^{\prime \prime }$
par
![]() $x^{\prime \prime }=[\frac{r^{\prime }+r^{\prime \prime }+1}{2}]$
. On a
$x^{\prime \prime }=[\frac{r^{\prime }+r^{\prime \prime }+1}{2}]$
. On a
![]() $x^{\prime }=\frac{r^{\prime }+r^{\prime \prime }-a}{2}$
et
$x^{\prime }=\frac{r^{\prime }+r^{\prime \prime }-a}{2}$
et
![]() $x^{\prime \prime }=\frac{r^{\prime }+r^{\prime \prime }+a}{2}$
. Un calcul algébrique montre que
$x^{\prime \prime }=\frac{r^{\prime }+r^{\prime \prime }+a}{2}$
. Un calcul algébrique montre que
D’où la première égalité puisque
![]() $a^{2}=a$
. La seconde égalité en résulte, en changeant
$a^{2}=a$
. La seconde égalité en résulte, en changeant
![]() $r^{\prime \prime }$
en
$r^{\prime \prime }$
en
![]() $-r^{\prime \prime }$
.◻
$-r^{\prime \prime }$
.◻
On définit
![]() $r_{+}^{\prime }$
et
$r_{+}^{\prime }$
et
![]() $r_{-}^{\prime }$
par
$r_{-}^{\prime }$
par
si
![]() $r^{\prime }\equiv r^{\prime \prime }\,\,\text{mod}\,\,2\,\mathbb{Z}$
,
$r^{\prime }\equiv r^{\prime \prime }\,\,\text{mod}\,\,2\,\mathbb{Z}$
,
![]() $r_{+}^{\prime }=r^{\prime }+1$
,
$r_{+}^{\prime }=r^{\prime }+1$
,
![]() $r_{-}^{\prime }=r^{\prime }$
;
$r_{-}^{\prime }=r^{\prime }$
;
si
![]() $r^{\prime }\not \equiv r^{\prime \prime }\,\,\text{mod}\,\,2\,\mathbb{Z}$
,
$r^{\prime }\not \equiv r^{\prime \prime }\,\,\text{mod}\,\,2\,\mathbb{Z}$
,
![]() $r_{+}^{\prime }=r^{\prime }$
,
$r_{+}^{\prime }=r^{\prime }$
,
![]() $r_{-}^{\prime }=r^{\prime }+1$
.
$r_{-}^{\prime }=r^{\prime }+1$
.
Autrement dit,
![]() $r_{+}^{\prime }=r^{\prime }+1-a$
et
$r_{+}^{\prime }=r^{\prime }+1-a$
et
![]() $r_{-}^{\prime }=r^{\prime }+a$
. En remplaçant le couple
$r_{-}^{\prime }=r^{\prime }+a$
. En remplaçant le couple
![]() $(r^{\prime },r^{\prime \prime })$
par
$(r^{\prime },r^{\prime \prime })$
par
![]() $(r_{1}^{\prime },r_{1}^{\prime \prime })$
ou
$(r_{1}^{\prime },r_{1}^{\prime \prime })$
ou
![]() $(r_{2}^{\prime },r_{2}^{\prime \prime })$
, on définit de même
$(r_{2}^{\prime },r_{2}^{\prime \prime })$
, on définit de même
![]() $r_{1,+}^{\prime }$
et
$r_{1,+}^{\prime }$
et
![]() $r_{1,-}^{\prime }$
ou
$r_{1,-}^{\prime }$
ou
![]() $r_{2,+}^{\prime }$
et
$r_{2,+}^{\prime }$
et
![]() $r_{2,-}^{\prime }$
.
$r_{2,-}^{\prime }$
.
(3) On a les égalités
![]() $r_{1,+}^{\prime }+r_{1}^{\prime \prime }=|r_{+}^{\prime }+r^{\prime \prime }|$
,
$r_{1,+}^{\prime }+r_{1}^{\prime \prime }=|r_{+}^{\prime }+r^{\prime \prime }|$
,
![]() $r_{1,-}^{\prime }+r_{1}^{\prime \prime }=|r_{-}^{\prime }+r^{\prime \prime }|$
,
$r_{1,-}^{\prime }+r_{1}^{\prime \prime }=|r_{-}^{\prime }+r^{\prime \prime }|$
,
![]() $r_{2,+}^{\prime }+r_{2}^{\prime \prime }=|r_{+}^{\prime }-r^{\prime \prime }|$
,
$r_{2,+}^{\prime }+r_{2}^{\prime \prime }=|r_{+}^{\prime }-r^{\prime \prime }|$
,
![]() $r_{2,-}^{\prime }+r_{2}^{\prime \prime }=|r_{-}^{\prime }-r^{\prime \prime }|$
.
$r_{2,-}^{\prime }+r_{2}^{\prime \prime }=|r_{-}^{\prime }-r^{\prime \prime }|$
.
Preuve.
De même que l’on a défini
![]() $a$
et
$a$
et
![]() $A$
pour
$A$
pour
![]() $(r^{\prime },r^{\prime \prime })$
, on définit
$(r^{\prime },r^{\prime \prime })$
, on définit
![]() $a_{1}$
et
$a_{1}$
et
![]() $A_{1}$
pour
$A_{1}$
pour
![]() $(r_{1}^{\prime },r_{1}^{\prime \prime })$
, et
$(r_{1}^{\prime },r_{1}^{\prime \prime })$
, et
![]() $a_{2}$
et
$a_{2}$
et
![]() $A_{2}$
pour
$A_{2}$
pour
![]() $(r_{2}^{\prime },r_{2}^{\prime \prime })$
. Supposons que
$(r_{2}^{\prime },r_{2}^{\prime \prime })$
. Supposons que
![]() $r^{\prime \prime }\geqslant 0$
. Alors
$r^{\prime \prime }\geqslant 0$
. Alors
![]() $r_{1}^{\prime }=[\frac{r^{\prime }+r^{\prime \prime }}{2}]=\frac{r^{\prime }+r^{\prime \prime }-a}{2}$
et
$r_{1}^{\prime }=[\frac{r^{\prime }+r^{\prime \prime }}{2}]=\frac{r^{\prime }+r^{\prime \prime }-a}{2}$
et
![]() $r_{1}^{\prime \prime }=[\frac{r^{\prime }+r^{\prime \prime }+1}{2}]=\frac{r^{\prime }+r^{\prime \prime }+a}{2}$
. Si
$r_{1}^{\prime \prime }=[\frac{r^{\prime }+r^{\prime \prime }+1}{2}]=\frac{r^{\prime }+r^{\prime \prime }+a}{2}$
. Si
![]() $a=0$
,
$a=0$
,
![]() $r_{1}^{\prime }=r_{1}^{\prime \prime }$
donc
$r_{1}^{\prime }=r_{1}^{\prime \prime }$
donc
![]() $a_{1}=A_{1}=0$
. Si
$a_{1}=A_{1}=0$
. Si
![]() $a=1$
,
$a=1$
,
![]() $r_{1}^{\prime }=r_{1}^{\prime \prime }-1$
donc
$r_{1}^{\prime }=r_{1}^{\prime \prime }-1$
donc
![]() $a_{1}=A_{1}=1$
. On a donc
$a_{1}=A_{1}=1$
. On a donc
![]() $a_{1}=A_{1}=a$
quel que soit
$a_{1}=A_{1}=a$
quel que soit
![]() $a$
. D’où
$a$
. D’où
![]() $r_{1,+}^{\prime }=r_{1}^{\prime }+1-a_{1}=\frac{r^{\prime }+r^{\prime \prime }-a}{2}+1-a$
et
$r_{1,+}^{\prime }=r_{1}^{\prime }+1-a_{1}=\frac{r^{\prime }+r^{\prime \prime }-a}{2}+1-a$
et
![]() $r_{1,-}^{\prime }=r_{1}^{\prime }+a_{1}=\frac{r^{\prime }+r^{\prime \prime }-a}{2}+a$
. On calcule alors
$r_{1,-}^{\prime }=r_{1}^{\prime }+a_{1}=\frac{r^{\prime }+r^{\prime \prime }-a}{2}+a$
. On calcule alors
 $$\begin{eqnarray}\displaystyle r_{1,+}^{\prime }+r_{1}^{\prime \prime } & = & \displaystyle \frac{r^{\prime }+r^{\prime \prime }-a}{2}+1-a+\frac{r^{\prime }+r^{\prime \prime }+a}{2}=r^{\prime }+r^{\prime \prime }+1-a\nonumber\\ \displaystyle & = & \displaystyle r_{+}^{\prime }+r^{\prime \prime }=|r_{+}^{\prime }+r^{\prime \prime }|,\nonumber\\ \displaystyle r_{1,-}^{\prime }+r_{1}^{\prime \prime } & = & \displaystyle \frac{r^{\prime }+r^{\prime \prime }-a}{2}+a+\frac{r^{\prime }+r^{\prime \prime }+a}{2}=r^{\prime }+r^{\prime \prime }+a\nonumber\\ \displaystyle & = & \displaystyle r_{-}^{\prime }+r^{\prime \prime }=|r_{-}^{\prime }+r^{\prime \prime }|.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle r_{1,+}^{\prime }+r_{1}^{\prime \prime } & = & \displaystyle \frac{r^{\prime }+r^{\prime \prime }-a}{2}+1-a+\frac{r^{\prime }+r^{\prime \prime }+a}{2}=r^{\prime }+r^{\prime \prime }+1-a\nonumber\\ \displaystyle & = & \displaystyle r_{+}^{\prime }+r^{\prime \prime }=|r_{+}^{\prime }+r^{\prime \prime }|,\nonumber\\ \displaystyle r_{1,-}^{\prime }+r_{1}^{\prime \prime } & = & \displaystyle \frac{r^{\prime }+r^{\prime \prime }-a}{2}+a+\frac{r^{\prime }+r^{\prime \prime }+a}{2}=r^{\prime }+r^{\prime \prime }+a\nonumber\\ \displaystyle & = & \displaystyle r_{-}^{\prime }+r^{\prime \prime }=|r_{-}^{\prime }+r^{\prime \prime }|.\nonumber\end{eqnarray}$$
Ce sont les deux premières égalités de (3). Supposons que
![]() $b=0$
. Alors
$b=0$
. Alors
![]() $r_{2}^{\prime }=[\frac{r^{\prime }-r^{\prime \prime }}{2}]=\frac{r^{\prime }-r^{\prime \prime }-a}{2}$
et
$r_{2}^{\prime }=[\frac{r^{\prime }-r^{\prime \prime }}{2}]=\frac{r^{\prime }-r^{\prime \prime }-a}{2}$
et
![]() $r_{2}^{\prime \prime }=[\frac{r^{\prime }-r^{\prime \prime }+1}{2}]=\frac{r^{\prime }-r^{\prime \prime }+a}{2}$
. Le calcul est le même que précédemment, on a simplement changé
$r_{2}^{\prime \prime }=[\frac{r^{\prime }-r^{\prime \prime }+1}{2}]=\frac{r^{\prime }-r^{\prime \prime }+a}{2}$
. Le calcul est le même que précédemment, on a simplement changé
![]() $r^{\prime \prime }$
en
$r^{\prime \prime }$
en
![]() $-r^{\prime \prime }$
dans les formules (en particulier, on a
$-r^{\prime \prime }$
dans les formules (en particulier, on a
![]() $a_{2}=A_{2}=a$
si
$a_{2}=A_{2}=a$
si
![]() $b=0$
). Supposons que
$b=0$
). Supposons que
![]() $b=1$
. Alors
$b=1$
. Alors
![]() $r_{2}^{\prime }=-1-[\frac{r^{\prime }-r^{\prime \prime }}{2}]=-1+\frac{r^{\prime \prime }-r^{\prime }+a}{2}$
et
$r_{2}^{\prime }=-1-[\frac{r^{\prime }-r^{\prime \prime }}{2}]=-1+\frac{r^{\prime \prime }-r^{\prime }+a}{2}$
et
![]() $r_{2}^{\prime \prime }=-[\frac{r^{\prime }-r^{\prime \prime }+1}{2}]=\frac{r^{\prime \prime }-r^{\prime }-a}{2}$
. On constate que cette fois,
$r_{2}^{\prime \prime }=-[\frac{r^{\prime }-r^{\prime \prime }+1}{2}]=\frac{r^{\prime \prime }-r^{\prime }-a}{2}$
. On constate que cette fois,
![]() $a_{2}=A_{2}=1-a$
. Alors
$a_{2}=A_{2}=1-a$
. Alors
![]() $r_{2,+}^{\prime }=r_{2}^{\prime }+1-a_{2}=r_{2}^{\prime }+a=\frac{r^{\prime \prime }-r^{\prime }+a}{2}+a-1$
et
$r_{2,+}^{\prime }=r_{2}^{\prime }+1-a_{2}=r_{2}^{\prime }+a=\frac{r^{\prime \prime }-r^{\prime }+a}{2}+a-1$
et
![]() $r_{2,-}^{\prime }=r_{2}^{\prime }+a_{2}=r_{2}^{\prime }+1-a=\frac{r^{\prime \prime }-r^{\prime }+a}{2}-a$
. On calcule alors
$r_{2,-}^{\prime }=r_{2}^{\prime }+a_{2}=r_{2}^{\prime }+1-a=\frac{r^{\prime \prime }-r^{\prime }+a}{2}-a$
. On calcule alors
 $$\begin{eqnarray}\displaystyle r_{2,+}^{\prime }+r_{2}^{\prime \prime } & = & \displaystyle \frac{r^{\prime \prime }-r^{\prime }+a}{2}+a-1+\frac{r^{\prime \prime }-r^{\prime }-a}{2}=r^{\prime \prime }-r^{\prime }+a-1\nonumber\\ \displaystyle & = & \displaystyle r^{\prime \prime }-r_{+}^{\prime }=|r_{+}^{\prime }-r^{\prime \prime }|,\nonumber\\ \displaystyle r_{2,-}^{\prime }+r_{2}^{\prime \prime } & = & \displaystyle \frac{r^{\prime \prime }-r^{\prime }+a}{2}-a+\frac{r^{\prime \prime }-r^{\prime }-a}{2}=r^{\prime \prime }-r^{\prime }-a\nonumber\\ \displaystyle & = & \displaystyle r^{\prime \prime }-r_{-}^{\prime }=|r_{-}^{\prime }-r^{\prime \prime }|.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle r_{2,+}^{\prime }+r_{2}^{\prime \prime } & = & \displaystyle \frac{r^{\prime \prime }-r^{\prime }+a}{2}+a-1+\frac{r^{\prime \prime }-r^{\prime }-a}{2}=r^{\prime \prime }-r^{\prime }+a-1\nonumber\\ \displaystyle & = & \displaystyle r^{\prime \prime }-r_{+}^{\prime }=|r_{+}^{\prime }-r^{\prime \prime }|,\nonumber\\ \displaystyle r_{2,-}^{\prime }+r_{2}^{\prime \prime } & = & \displaystyle \frac{r^{\prime \prime }-r^{\prime }+a}{2}-a+\frac{r^{\prime \prime }-r^{\prime }-a}{2}=r^{\prime \prime }-r^{\prime }-a\nonumber\\ \displaystyle & = & \displaystyle r^{\prime \prime }-r_{-}^{\prime }=|r_{-}^{\prime }-r^{\prime \prime }|.\nonumber\end{eqnarray}$$
Ce sont encore les deux dernières égalités de (3). On a supposé que
![]() $r^{\prime \prime }\geqslant 0$
. Si
$r^{\prime \prime }\geqslant 0$
. Si
![]() $r^{\prime \prime }\leqslant 0$
, on a remarqué que nos couples
$r^{\prime \prime }\leqslant 0$
, on a remarqué que nos couples
![]() $(r_{1}^{\prime },r_{1}^{\prime \prime })$
et
$(r_{1}^{\prime },r_{1}^{\prime \prime })$
et
![]() $(r_{2}^{\prime },r_{2}^{\prime \prime })$
sont les mêmes que ceux déduits du couple
$(r_{2}^{\prime },r_{2}^{\prime \prime })$
sont les mêmes que ceux déduits du couple
![]() $(r^{\prime },-r^{\prime \prime })$
, à cela près que l’on doit échanger les indices
$(r^{\prime },-r^{\prime \prime })$
, à cela près que l’on doit échanger les indices
![]() $1$
et
$1$
et
![]() $2$
. Les égalités (3) pour
$2$
. Les égalités (3) pour
![]() $(r^{\prime },r^{\prime \prime })$
se déduisent par ce changement des mêmes égalités que l’on vient de démontrer pour le couple
$(r^{\prime },r^{\prime \prime })$
se déduisent par ce changement des mêmes égalités que l’on vient de démontrer pour le couple
![]() $(r^{\prime },-r^{\prime \prime })$
.◻
$(r^{\prime },-r^{\prime \prime })$
.◻
Définissons un nombre
![]() $u$
par
$u$
par
si
![]() $|r^{\prime \prime }|\leqslant r^{\prime }$
,
$|r^{\prime \prime }|\leqslant r^{\prime }$
,
![]() $u=\frac{r^{\prime 2}-r^{\prime }}{2}+\frac{r^{\prime \prime 2}-|r^{\prime \prime }|}{2}+\frac{r_{+}^{\prime }-|r^{\prime \prime }|-1}{2}$
,
$u=\frac{r^{\prime 2}-r^{\prime }}{2}+\frac{r^{\prime \prime 2}-|r^{\prime \prime }|}{2}+\frac{r_{+}^{\prime }-|r^{\prime \prime }|-1}{2}$
,
si
![]() $r^{\prime }<|r^{\prime \prime }|$
,
$r^{\prime }<|r^{\prime \prime }|$
,
![]() $u=\frac{r^{\prime 2}-r^{\prime }}{2}+\frac{r^{\prime \prime 2}-|r^{\prime \prime }|}{2}+r^{\prime }+r^{\prime \prime }+1$
.
$u=\frac{r^{\prime 2}-r^{\prime }}{2}+\frac{r^{\prime \prime 2}-|r^{\prime \prime }|}{2}+r^{\prime }+r^{\prime \prime }+1$
.
Posons
![]() $U=(-1)^{r^{\prime \prime }}\operatorname{sgn}(-1)^{u}$
. On définit de même
$U=(-1)^{r^{\prime \prime }}\operatorname{sgn}(-1)^{u}$
. On définit de même
![]() $u_{1}$
,
$u_{1}$
,
![]() $U_{1}$
et
$U_{1}$
et
![]() $u_{2}$
,
$u_{2}$
,
![]() $U_{2}$
.
$U_{2}$
.
(4) On a l’égalité
![]() $U=U_{1}U_{2}$
.
$U=U_{1}U_{2}$
.
Preuve.
Comme dans la preuve précédente, on peut supposer que
![]() $r^{\prime \prime }\geqslant 0$
. On a
$r^{\prime \prime }\geqslant 0$
. On a
![]() $(-1)^{r^{\prime \prime }}=(-1)^{r_{1}^{\prime \prime }+r_{2}^{\prime \prime }}$
d’après (1) et il suffit de démontrer que
$(-1)^{r^{\prime \prime }}=(-1)^{r_{1}^{\prime \prime }+r_{2}^{\prime \prime }}$
d’après (1) et il suffit de démontrer que
![]() $u\equiv u_{1}+u_{2}\,\,\text{mod}\,\,2\,\mathbb{Z}$
. Considérons l’expression qui définit
$u\equiv u_{1}+u_{2}\,\,\text{mod}\,\,2\,\mathbb{Z}$
. Considérons l’expression qui définit
![]() $u$
dans le cas
$u$
dans le cas
![]() $r^{\prime \prime }\leqslant r^{\prime }$
. On y remplace
$r^{\prime \prime }\leqslant r^{\prime }$
. On y remplace
![]() $r_{+}^{\prime }$
par
$r_{+}^{\prime }$
par
![]() $r^{\prime }+1-a$
. On peut ajouter
$r^{\prime }+1-a$
. On peut ajouter
![]() $r^{\prime }+r^{\prime \prime }+a$
qui est pair et on calcule
$r^{\prime }+r^{\prime \prime }+a$
qui est pair et on calcule
![]() $u\equiv \frac{r^{\prime 2}+r^{\prime \prime 2}+r^{\prime }}{2}+\frac{r^{\prime }+a}{2}\,\,\text{mod}\,\,2\,\mathbb{Z}$
. La différence entre l’expression de
$u\equiv \frac{r^{\prime 2}+r^{\prime \prime 2}+r^{\prime }}{2}+\frac{r^{\prime }+a}{2}\,\,\text{mod}\,\,2\,\mathbb{Z}$
. La différence entre l’expression de
![]() $u$
dans le cas
$u$
dans le cas
![]() $r^{\prime }<r^{\prime \prime }$
et cette expression dans le cas
$r^{\prime }<r^{\prime \prime }$
et cette expression dans le cas
![]() $r^{\prime \prime }\leqslant r^{\prime }$
est
$r^{\prime \prime }\leqslant r^{\prime }$
est
 $$\begin{eqnarray}\displaystyle r^{\prime }+r^{\prime \prime }+1-\frac{r_{+}^{\prime }-r^{\prime \prime }-1}{2} & \equiv & \displaystyle r^{\prime }-r^{\prime \prime }+1-\frac{r^{\prime }-a-r^{\prime \prime }}{2}\nonumber\\ \displaystyle & \equiv & \displaystyle \frac{r^{\prime }+a-r^{\prime \prime }}{2}+1\,\,\text{mod}\,\,2\,\mathbb{Z}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle r^{\prime }+r^{\prime \prime }+1-\frac{r_{+}^{\prime }-r^{\prime \prime }-1}{2} & \equiv & \displaystyle r^{\prime }-r^{\prime \prime }+1-\frac{r^{\prime }-a-r^{\prime \prime }}{2}\nonumber\\ \displaystyle & \equiv & \displaystyle \frac{r^{\prime }+a-r^{\prime \prime }}{2}+1\,\,\text{mod}\,\,2\,\mathbb{Z}.\nonumber\end{eqnarray}$$
On obtient alors la congruence
en tout cas. La demi-somme des membres de droite de (2) vaut
![]() $\frac{r^{\prime 2}+r^{\prime \prime 2}+r^{\prime }}{2}$
. En utilisant (2), on obtient
$\frac{r^{\prime 2}+r^{\prime \prime 2}+r^{\prime }}{2}$
. En utilisant (2), on obtient
puis, en utilisant les analogues de (5) pour
![]() $u_{1}$
et
$u_{1}$
et
![]() $u_{2}$
,
$u_{2}$
,
 $$\begin{eqnarray}\displaystyle u & \equiv & \displaystyle u_{1}+u_{2}+\frac{r^{\prime }+a-r_{1}^{\prime }-a_{1}-r_{2}^{\prime }-a_{2}}{2}+A\biggl(\frac{r^{\prime }+a-r^{\prime \prime }}{2}+1\biggr)\nonumber\\ \displaystyle & & \displaystyle -\,A_{1}\biggl(\frac{r_{1}^{\prime }+a_{1}-r_{1}^{\prime \prime }}{2}+1\biggr)-A_{2}\biggl(\frac{r_{2}^{\prime }+a_{2}-r_{2}^{\prime \prime }}{2}+1\biggr)\,\,\text{mod}\,\,2\,\mathbb{Z}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle u & \equiv & \displaystyle u_{1}+u_{2}+\frac{r^{\prime }+a-r_{1}^{\prime }-a_{1}-r_{2}^{\prime }-a_{2}}{2}+A\biggl(\frac{r^{\prime }+a-r^{\prime \prime }}{2}+1\biggr)\nonumber\\ \displaystyle & & \displaystyle -\,A_{1}\biggl(\frac{r_{1}^{\prime }+a_{1}-r_{1}^{\prime \prime }}{2}+1\biggr)-A_{2}\biggl(\frac{r_{2}^{\prime }+a_{2}-r_{2}^{\prime \prime }}{2}+1\biggr)\,\,\text{mod}\,\,2\,\mathbb{Z}.\nonumber\end{eqnarray}$$
Cette expression se simplifie : puisque
![]() $r_{1}^{\prime }=r_{1}^{\prime \prime }$
ou
$r_{1}^{\prime }=r_{1}^{\prime \prime }$
ou
![]() $r_{1}^{\prime \prime }-1$
, on a toujours
$r_{1}^{\prime \prime }-1$
, on a toujours
![]() $r_{1,-}^{\prime }=r_{1}^{\prime \prime }$
. De même,
$r_{1,-}^{\prime }=r_{1}^{\prime \prime }$
. De même,
![]() $r_{2,-}^{\prime }=r_{2}^{\prime \prime }$
. On a aussi remarqué que
$r_{2,-}^{\prime }=r_{2}^{\prime \prime }$
. On a aussi remarqué que
![]() $a_{1}=A_{1}=a$
. D’où
$a_{1}=A_{1}=a$
. D’où
Si
![]() $A=0$
, on a aussi
$A=0$
, on a aussi
![]() $a_{2}=A_{2}=a$
,
$a_{2}=A_{2}=a$
,
![]() $r_{1}^{\prime }=\frac{r^{\prime }+r^{\prime \prime }-a}{2}$
,
$r_{1}^{\prime }=\frac{r^{\prime }+r^{\prime \prime }-a}{2}$
,
![]() $r_{1}^{\prime \prime }=\frac{r^{\prime }-r^{\prime \prime }-a}{2}$
. Si
$r_{1}^{\prime \prime }=\frac{r^{\prime }-r^{\prime \prime }-a}{2}$
. Si
![]() $A=1$
, on a
$A=1$
, on a
![]() $a_{2}=A_{2}=1-a$
,
$a_{2}=A_{2}=1-a$
,
![]() $r_{1}^{\prime }=\frac{r^{\prime }+r^{\prime \prime }-a}{2}$
,
$r_{1}^{\prime }=\frac{r^{\prime }+r^{\prime \prime }-a}{2}$
,
![]() $r_{1}^{\prime \prime }=-1-\frac{r^{\prime }-r^{\prime \prime }-a}{2}$
. On calcule l’expression ci-dessus dans les deux cas et on conclut que
$r_{1}^{\prime \prime }=-1-\frac{r^{\prime }-r^{\prime \prime }-a}{2}$
. On calcule l’expression ci-dessus dans les deux cas et on conclut que
![]() $u\equiv u_{1}+u_{2}\,\,\text{mod}\,\,2\,\mathbb{Z}$
. Cela prouve (4).◻
$u\equiv u_{1}+u_{2}\,\,\text{mod}\,\,2\,\mathbb{Z}$
. Cela prouve (4).◻
Index des notations
![]() $C_{\operatorname{cusp}}^{\infty }(G_{\sharp }(F))$
1.2 ;
$C_{\operatorname{cusp}}^{\infty }(G_{\sharp }(F))$
1.2 ;
![]() $\mathbb{C}[\hat{\mathfrak{S}}_{m}]_{U-\operatorname{cusp}}$
2.3 ;
$\mathbb{C}[\hat{\mathfrak{S}}_{m}]_{U-\operatorname{cusp}}$
2.3 ;
![]() ${\mathcal{E}}$
2.4 ;
${\mathcal{E}}$
2.4 ;
![]() $f_{\unicode[STIX]{x1D70B}}$
1.1 ;
$f_{\unicode[STIX]{x1D70B}}$
1.1 ;
![]() $\unicode[STIX]{x1D711}_{w}$
2.1 ;
$\unicode[STIX]{x1D711}_{w}$
2.1 ;
![]() $\hat{i} _{\sharp }[a,e,u]$
2.4 ;
$\hat{i} _{\sharp }[a,e,u]$
2.4 ;
![]() $\unicode[STIX]{x1D6F9}$
1.1 ;
$\unicode[STIX]{x1D6F9}$
1.1 ;
![]() ${\mathcal{Q}}(r^{\prime },r^{\prime \prime })^{\operatorname{Lie}}$
2.1, 2.2, 2.3 ;
${\mathcal{Q}}(r^{\prime },r^{\prime \prime })^{\operatorname{Lie}}$
2.1, 2.2, 2.3 ;
![]() $\operatorname{sgn}$
2.1 ;
$\operatorname{sgn}$
2.1 ;
![]() $\unicode[STIX]{x1D6E9}_{\unicode[STIX]{x1D70B}}$
1.1 ;
$\unicode[STIX]{x1D6E9}_{\unicode[STIX]{x1D70B}}$
1.1 ;
![]() ${\mathcal{U}}$
2.4 ;
${\mathcal{U}}$
2.4 ;
![]() $X^{\unicode[STIX]{x1D701}}(a,e,u)$
2.4.
$X^{\unicode[STIX]{x1D701}}(a,e,u)$
2.4.
Index des notations de [Reference Waldspurger11]
![]() $\mathbb{C}[X]$
1.4 ;
$\mathbb{C}[X]$
1.4 ;
![]() $C_{n^{\prime }}^{\prime }$
1.5 ;
$C_{n^{\prime }}^{\prime }$
1.5 ;
![]() $C_{n^{\prime \prime },\sharp }^{^{\prime \prime }\pm }$
1.5 ;
$C_{n^{\prime \prime },\sharp }^{^{\prime \prime }\pm }$
1.5 ;
![]() $C_{n^{\prime \prime }}^{\prime \prime }$
1.5 ;
$C_{n^{\prime \prime }}^{\prime \prime }$
1.5 ;
![]() $C^{\operatorname{GL}(m)}$
1.5 ;
$C^{\operatorname{GL}(m)}$
1.5 ;
![]() $\mathbb{C}[{\hat{W}}_{N}]_{\operatorname{cusp}}$
1.8 ;
$\mathbb{C}[{\hat{W}}_{N}]_{\operatorname{cusp}}$
1.8 ;
![]() $D(n)$
1.2 ;
$D(n)$
1.2 ;
![]() $D_{\operatorname{iso}}(n)$
1.2 ;
$D_{\operatorname{iso}}(n)$
1.2 ;
![]() $D_{\operatorname{an}}(n)$
1.2 ;
$D_{\operatorname{an}}(n)$
1.2 ;
![]() $D$
1.7 ;
$D$
1.7 ;
![]() $D^{\operatorname{par}}$
1.7 ;
$D^{\operatorname{par}}$
1.7 ;
![]() $\unicode[STIX]{x1D702}(Q)$
1.1 ;
$\unicode[STIX]{x1D702}(Q)$
1.1 ;
![]() $\unicode[STIX]{x1D702}^{+}(Q)$
1.1 ;
$\unicode[STIX]{x1D702}^{+}(Q)$
1.1 ;
![]() $\unicode[STIX]{x1D702}^{-}(Q)$
1.1 ;
$\unicode[STIX]{x1D702}^{-}(Q)$
1.1 ;
![]() $Ell_{\operatorname{unip}}$
1.4 ;
$Ell_{\operatorname{unip}}$
1.4 ;
![]() $\mathfrak{Ell}_{\operatorname{unip}}$
1.4 ;
$\mathfrak{Ell}_{\operatorname{unip}}$
1.4 ;
![]() $\mathfrak{Endo}_{\operatorname{tunip}}$
2.1 ;
$\mathfrak{Endo}_{\operatorname{tunip}}$
2.1 ;
![]() $\mathfrak{Endo}_{\operatorname{unip}\!{-}\text{quad}}$
2.2 ;
$\mathfrak{Endo}_{\operatorname{unip}\!{-}\text{quad}}$
2.2 ;
![]() $\mathfrak{Endo}_{\operatorname{unip}\!{-}\text{quad}}^{red}$
2.2 ;
$\mathfrak{Endo}_{\operatorname{unip}\!{-}\text{quad}}^{red}$
2.2 ;
![]() $\mathfrak{Endo}_{\operatorname{unip},\operatorname{disc}}$
2.4 ;
$\mathfrak{Endo}_{\operatorname{unip},\operatorname{disc}}$
2.4 ;
![]() ${\mathcal{F}}^{L}$
1.9 ;
${\mathcal{F}}^{L}$
1.9 ;
![]() ${\mathcal{F}}^{\operatorname{par}}$
1.9 ;
${\mathcal{F}}^{\operatorname{par}}$
1.9 ;
![]() ${\mathcal{F}}$
2.3 :
${\mathcal{F}}$
2.3 :
![]() $\mathfrak{F}^{\operatorname{par}}$
2.3 ;
$\mathfrak{F}^{\operatorname{par}}$
2.3 ;
![]() $G_{\operatorname{iso}}$
1.1 ;
$G_{\operatorname{iso}}$
1.1 ;
![]() $G_{\operatorname{an}}$
1.1 ;
$G_{\operatorname{an}}$
1.1 ;
![]() $\unicode[STIX]{x1D6E4}$
1.8 ;
$\unicode[STIX]{x1D6E4}$
1.8 ;
![]() $\boldsymbol{\unicode[STIX]{x1D6E4}}$
1.8 ;
$\boldsymbol{\unicode[STIX]{x1D6E4}}$
1.8 ;
![]() $\tilde{\operatorname{GL}}(2n)$
2.1 ;
$\tilde{\operatorname{GL}}(2n)$
2.1 ;
![]() $\operatorname{Irr}_{\operatorname{tunip}}$
1.3 ;
$\operatorname{Irr}_{\operatorname{tunip}}$
1.3 ;
![]() $\mathfrak{Irr}_{\operatorname{tunip}}$
1.3 ;
$\mathfrak{Irr}_{\operatorname{tunip}}$
1.3 ;
![]() $\operatorname{Irr}_{\operatorname{unip}\!{-}\text{quad}}$
1.3 ;
$\operatorname{Irr}_{\operatorname{unip}\!{-}\text{quad}}$
1.3 ;
![]() $\mathfrak{Irr}_{\operatorname{unip}\!{-}\text{quad}}$
1.3 ;
$\mathfrak{Irr}_{\operatorname{unip}\!{-}\text{quad}}$
1.3 ;
![]() $\operatorname{Jord}(\unicode[STIX]{x1D706})$
1.3 ;
$\operatorname{Jord}(\unicode[STIX]{x1D706})$
1.3 ;
![]() $\operatorname{Jord}_{\text{bp}}(\unicode[STIX]{x1D706})$
1.3 ;
$\operatorname{Jord}_{\text{bp}}(\unicode[STIX]{x1D706})$
1.3 ;
![]() $\operatorname{Jord}_{\text{bp}}^{k}(\unicode[STIX]{x1D706})$
1.4 ;
$\operatorname{Jord}_{\text{bp}}^{k}(\unicode[STIX]{x1D706})$
1.4 ;
![]() $K_{n^{\prime },n^{\prime \prime }}^{\pm }$
1.2 ;
$K_{n^{\prime },n^{\prime \prime }}^{\pm }$
1.2 ;
![]() $k$
1.9 ;
$k$
1.9 ;
![]() $L^{\ast }$
1.1 ;
$L^{\ast }$
1.1 ;
![]() $L_{n^{\prime },n^{\prime \prime }}$
1.2 ;
$L_{n^{\prime },n^{\prime \prime }}$
1.2 ;
![]() $l(\unicode[STIX]{x1D706})$
1.3 ;
$l(\unicode[STIX]{x1D706})$
1.3 ;
![]() $\text{mult}_{\unicode[STIX]{x1D706}}$
1.3 ;
$\text{mult}_{\unicode[STIX]{x1D706}}$
1.3 ;
![]() $\mathfrak{o}$
1.1 ;
$\mathfrak{o}$
1.1 ;
![]() $O^{+}(Q)$
1.1 ;
$O^{+}(Q)$
1.1 ;
![]() $O^{-}(Q)$
1.1 ;
$O^{-}(Q)$
1.1 ;
![]() $\unicode[STIX]{x1D71B}$
1.1 ;
$\unicode[STIX]{x1D71B}$
1.1 ;
![]() $\unicode[STIX]{x1D70B}_{n^{\prime },n^{\prime \prime }}$
1.3 ;
$\unicode[STIX]{x1D70B}_{n^{\prime },n^{\prime \prime }}$
1.3 ;
![]() ${\mathcal{P}}(N)$
1.3 ;
${\mathcal{P}}(N)$
1.3 ;
![]() ${\mathcal{P}}^{\text{symp}}(2N)$
1.3 ;
${\mathcal{P}}^{\text{symp}}(2N)$
1.3 ;
![]() $\boldsymbol{{\mathcal{P}}}^{\mathbf{symp}}(2N)$
1.3 ;
$\boldsymbol{{\mathcal{P}}}^{\mathbf{symp}}(2N)$
1.3 ;
![]() $\unicode[STIX]{x1D70B}(\unicode[STIX]{x1D706},s,\unicode[STIX]{x1D716})$
1.3 ;
$\unicode[STIX]{x1D70B}(\unicode[STIX]{x1D706},s,\unicode[STIX]{x1D716})$
1.3 ;
![]() $\unicode[STIX]{x1D70B}(\unicode[STIX]{x1D706}^{+},\unicode[STIX]{x1D716}^{+},\unicode[STIX]{x1D706}^{-},\unicode[STIX]{x1D716}^{-})$
1.3 ;
$\unicode[STIX]{x1D70B}(\unicode[STIX]{x1D706}^{+},\unicode[STIX]{x1D716}^{+},\unicode[STIX]{x1D706}^{-},\unicode[STIX]{x1D716}^{-})$
1.3 ;
![]() $\unicode[STIX]{x1D70B}_{\text{ell}}(\unicode[STIX]{x1D706}^{+},\unicode[STIX]{x1D716}^{+},\unicode[STIX]{x1D706}^{-},\unicode[STIX]{x1D716}^{-})$
1.4 ;
$\unicode[STIX]{x1D70B}_{\text{ell}}(\unicode[STIX]{x1D706}^{+},\unicode[STIX]{x1D716}^{+},\unicode[STIX]{x1D706}^{-},\unicode[STIX]{x1D716}^{-})$
1.4 ;
![]() $\operatorname{proj}_{\operatorname{cusp}}$
1.5 ;
$\operatorname{proj}_{\operatorname{cusp}}$
1.5 ;
![]() ${\mathcal{P}}({\leqslant}n)$
1.5 ;
${\mathcal{P}}({\leqslant}n)$
1.5 ;
![]() ${\mathcal{P}}_{k}(N)$
1.8 ;
${\mathcal{P}}_{k}(N)$
1.8 ;
![]() $\unicode[STIX]{x1D6F1}(\unicode[STIX]{x1D706},s,h)$
2.1 ;
$\unicode[STIX]{x1D6F1}(\unicode[STIX]{x1D706},s,h)$
2.1 ;
![]() $\unicode[STIX]{x1D6F1}^{st}(\unicode[STIX]{x1D706}^{+},\unicode[STIX]{x1D706}^{-})$
2.4 ;
$\unicode[STIX]{x1D6F1}^{st}(\unicode[STIX]{x1D706}^{+},\unicode[STIX]{x1D706}^{-})$
2.4 ;
![]() ${\mathcal{P}}^{\text{symp},\operatorname{disc}}(2n)$
2.4 ;
${\mathcal{P}}^{\text{symp},\operatorname{disc}}(2n)$
2.4 ;
![]() $Q_{\operatorname{iso}}$
1.1 ;
$Q_{\operatorname{iso}}$
1.1 ;
![]() $Q_{\operatorname{an}}$
1.1 ;
$Q_{\operatorname{an}}$
1.1 ;
![]() $\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D706}}$
1.3 ;
$\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D706}}$
1.3 ;
![]() ${\mathcal{R}}^{\operatorname{par}}$
1.5 ;
${\mathcal{R}}^{\operatorname{par}}$
1.5 ;
![]() ${\mathcal{R}}^{\text{par},\text{glob}}$
1.5 ;
${\mathcal{R}}^{\text{par},\text{glob}}$
1.5 ;
![]() ${\mathcal{R}}_{\operatorname{cusp}}^{\operatorname{par}}$
1.5 ;
${\mathcal{R}}_{\operatorname{cusp}}^{\operatorname{par}}$
1.5 ;
![]() ${\mathcal{R}}_{\mathbf{m}}^{\text{par},\text{glob}}$
1.5 ;
${\mathcal{R}}_{\mathbf{m}}^{\text{par},\text{glob}}$
1.5 ;
![]() ${\mathcal{R}}_{\mathbf{m},\operatorname{cusp}}^{\operatorname{par}}$
1.5 ;
${\mathcal{R}}_{\mathbf{m},\operatorname{cusp}}^{\operatorname{par}}$
1.5 ;
![]() $\text{res}_{m}^{\prime }$
1.5 ;
$\text{res}_{m}^{\prime }$
1.5 ;
![]() $\text{res}_{m}^{\prime \prime }$
1.5 ;
$\text{res}_{m}^{\prime \prime }$
1.5 ;
![]() $\text{res}_{m}$
1.5 et 1.8 ;
$\text{res}_{m}$
1.5 et 1.8 ;
![]() $\text{res}_{\mathbf{m}}$
1.5 ;
$\text{res}_{\mathbf{m}}$
1.5 ;
![]() ${\mathcal{R}}$
1.8 ;
${\mathcal{R}}$
1.8 ;
![]() ${\mathcal{R}}(\unicode[STIX]{x1D6FE})$
1.8 ;
${\mathcal{R}}(\unicode[STIX]{x1D6FE})$
1.8 ;
![]() ${\mathcal{R}}(\boldsymbol{\unicode[STIX]{x1D6FE}})$
1.8 ;
${\mathcal{R}}(\boldsymbol{\unicode[STIX]{x1D6FE}})$
1.8 ;
![]() ${\mathcal{R}}^{\text{glob}}$
1.8 ;
${\mathcal{R}}^{\text{glob}}$
1.8 ;
![]() ${\mathcal{R}}_{\operatorname{cusp}}$
1.8 ;
${\mathcal{R}}_{\operatorname{cusp}}$
1.8 ;
![]() $\text{Rep}$
1.9 ;
$\text{Rep}$
1.9 ;
![]() $\unicode[STIX]{x1D70C}\unicode[STIX]{x1D704}$
1.10 ;
$\unicode[STIX]{x1D70C}\unicode[STIX]{x1D704}$
1.10 ;
![]() $S(\unicode[STIX]{x1D706})$
1.3 ;
$S(\unicode[STIX]{x1D706})$
1.3 ;
![]() $\mathfrak{S}_{N}$
1.8 ;
$\mathfrak{S}_{N}$
1.8 ;
![]() $\hat{\mathfrak{S}}_{N}$
1.8 ;
$\hat{\mathfrak{S}}_{N}$
1.8 ;
![]() $\operatorname{sgn}$
1.8 ;
$\operatorname{sgn}$
1.8 ;
![]() $\operatorname{sgn}_{CD}$
1.8 ;
$\operatorname{sgn}_{CD}$
1.8 ;
![]() ${\mathcal{S}}_{n}$
1.11 ;
${\mathcal{S}}_{n}$
1.11 ;
![]() $\mathfrak{St}_{\operatorname{tunip}}$
2.1 ;
$\mathfrak{St}_{\operatorname{tunip}}$
2.1 ;
![]() $\mathfrak{St}_{\operatorname{unip}\!{-}\text{quad}}$
2.4 ;
$\mathfrak{St}_{\operatorname{unip}\!{-}\text{quad}}$
2.4 ;
![]() $\mathfrak{St}_{\operatorname{unip},\operatorname{disc}}$
2.4 ;
$\mathfrak{St}_{\operatorname{unip},\operatorname{disc}}$
2.4 ;
![]() $\operatorname{sgn}_{\operatorname{iso}}$
2.6 ;
$\operatorname{sgn}_{\operatorname{iso}}$
2.6 ;
![]() $\operatorname{sgn}_{\operatorname{an}}$
2.6 ;
$\operatorname{sgn}_{\operatorname{an}}$
2.6 ;
![]() $\operatorname{val}_{F}$
1.1 ;
$\operatorname{val}_{F}$
1.1 ;
![]() $V_{\operatorname{iso}}$
1.1 ;
$V_{\operatorname{iso}}$
1.1 ;
![]() $V_{\operatorname{an}}$
1.1 ;
$V_{\operatorname{an}}$
1.1 ;
![]() $W_{N}$
1.8 ;
$W_{N}$
1.8 ;
![]() ${\hat{W}}_{N}$
1.8 ;
${\hat{W}}_{N}$
1.8 ;
![]() $w_{\unicode[STIX]{x1D6FC}}$
1.8 ;
$w_{\unicode[STIX]{x1D6FC}}$
1.8 ;
![]() $w_{\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD}}$
1.8 ;
$w_{\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD}}$
1.8 ;
![]() $w_{\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD}^{\prime },\unicode[STIX]{x1D6FD}^{\prime \prime }}$
1.8 ;
$w_{\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD}^{\prime },\unicode[STIX]{x1D6FD}^{\prime \prime }}$
1.8 ;
![]() $Z(\unicode[STIX]{x1D706})$
1.3 ;
$Z(\unicode[STIX]{x1D706})$
1.3 ;
![]() $Z(\unicode[STIX]{x1D706},s)$
1.3 ;
$Z(\unicode[STIX]{x1D706},s)$
1.3 ;
![]() $\mathbf{Z}(\unicode[STIX]{x1D706},s)$
1.3 ;
$\mathbf{Z}(\unicode[STIX]{x1D706},s)$
1.3 ;
![]() $\mathbf{Z}(\unicode[STIX]{x1D706},s)^{\vee }$
1.3 ;
$\mathbf{Z}(\unicode[STIX]{x1D706},s)^{\vee }$
1.3 ;
![]() $|.|_{F}$
1.1.
$|.|_{F}$
1.1.