Hostname: page-component-848d4c4894-4hhp2 Total loading time: 0 Render date: 2024-05-01T02:38:56.664Z Has data issue: false hasContentIssue false
  • English
  • Français

The P-Harmonic Boundary and Energy-Finite Solutions of Δu = Pu

Published online by Cambridge University Press:  22 January 2016

Y.K. Kwon ,
L. Sario  and
J. Schiff
Y.K. Kwon
Affiliation:
University of California, Los Angeles
L. Sario
Affiliation:
University of California, Los Angeles
J. Schiff
Affiliation:
University of California, Los Angeles
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The P-harmonic boundary ΔP and the P-singular point s of a Riemannian manifold R have been shown to play an important role in the study of bounded energy-finite solutions of Δu = Pu (Nakai-Sario [7], Kwon-Sario [4], Kwon-Sario-Schiff [5]). The objective of the present paper is to establish, in terms of ΔP and s, properties of unbounded energy-finite solutions (PE-functions) and of limits of decreasing sequences of positive PE-functions (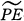-functions). Also, PE- and 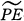-minimal functions will be discussed.

Type
Research Article
Information
Nagoya Mathematical Journal , Volume 42 , March 1971 , pp. 31 - 41
Copyright
Copyright © Editorial Board of Nagoya Mathematical Journal 1971

References

[1] Katz, M. Glasner-R., On the behavior of solutions of Δu = Pu at the Royden boundary, J. Analyse Math. 22 (1969), 343–354.Google Scholar
[2] Sario, Y.K. Kwon-L., A maximum principle for bounded harmonic functions on Riemannian spaces, Canad. J. Math. 22 (1970), 847–854.Google Scholar
[3] Sario, Y.K. Kwon-L., Harmonic functions on a subregion of a Riemannian manifold, J. Ind. Math. Soc. (to appear).Google Scholar
[4] Sario, Y.K. Kwon-L., The P-singular point of the Y-compactification for Δu = Pu, Bull. Amer. Math. Soc. (to appear).Google Scholar
[5] Scruff, Y.K. Kwon-L. Sario-J., Bounded energy-finite solutions of Δu = Pu on a Riemannian manifold, Nagoya. Math. J. (to appear).Google Scholar
[6] Nakai, M., A measure on the harmonic boundary of a Riemann surface, Nagoya Math. J. 17 (1960), 181–218.Google Scholar
[7] Sario, M. Nakai-L., A new operator for elliptic equations and the P-compactification for Δu = Pu, Math. Ann. 189 (1970), 242–256.Google Scholar
[8] Royden, H.L., The equation Δu = Pu and the classification of open Riemann surfaces, Ann. Acad. Sci. Fenn. Ser. A.I. 271 (1959), 27 pp.Google Scholar
[9] Nakai, L. Sario-M., Classification theory of Riemann surfaces, Springer, 1970, 446 pp.Google Scholar