Hostname: page-component-8448b6f56d-tj2md Total loading time: 0 Render date: 2024-04-25T00:36:14.741Z Has data issue: false hasContentIssue false
  • English
  • Français

ON THE MILNOR FIBRATION OF CERTAIN NEWTON DEGENERATE FUNCTIONS

Part of: Special varieties Singularities Local theory

Published online by Cambridge University Press:  01 December 2022

CHRISTOPHE EYRAL Open the ORCID record for CHRISTOPHE EYRAL [Opens in a new window]  and
MUTSUO OKA Open the ORCID record for MUTSUO OKA [Opens in a new window]
CHRISTOPHE EYRAL*
Affiliation:
Institute of Mathematics Polish Academy of Sciences Śniadeckich 8 00-656 Warsaw Poland
MUTSUO OKA
Affiliation:
Professor Emeritus of Tokyo Institute of Technology 3-19-8 Nakaochiai Shinjuku-ku Tokyo 161-0032 Japan okamutsuo@gmail.com
*
cheyral@impan.pl
Get access Rights & Permissions [Opens in a new window]

Abstract

It is well known that the diffeomorphism type of the Milnor fibration of a (Newton) nondegenerate polynomial function f is uniquely determined by the Newton boundary of f. In the present paper, we generalize this result to certain degenerate functions, namely we show that the diffeomorphism type of the Milnor fibration of a (possibly degenerate) polynomial function of the form 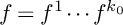$f=f^1\cdots f^{k_0}$ is uniquely determined by the Newton boundaries of 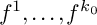$f^1,\ldots , f^{k_0}$ if 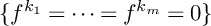$\{f^{k_1}=\cdots =f^{k_m}=0\}$ is a nondegenerate complete intersection variety for any 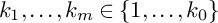$k_1,\ldots ,k_m\in \{1,\ldots , k_0\}$ .

MSC classification

Primary: 14B05: Singularities
Secondary: 14M10: Complete intersections 14M25: Toric varieties, Newton polyhedra 32S05: Local singularities 32S55: Milnor fibration; relations with knot theory
Type
Article
Information
Nagoya Mathematical Journal , Volume 250 , June 2023 , pp. 410 - 433
Check for updates
Copyright
© The Author(s) and the Polish Academy of Sciences, 2022. Published by Cambridge University Press on behalf of Foundation Nagoya Mathematical Journal

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Bernstein, D. N., The number of roots of a system of equations , Funktsional. Anal. i Prilozhen. 9 (1975), 1–4. English translation: Functional Anal. Appl. 9 (1975), 183–185 (1976).Google Scholar
Eyral, C. and Oka, M., Non-degenerate locally tame complete intersection varieties and geometry of non-isolated hypersurface singularities, J. Algebraic Geom. 31 (2022), 561–591.CrossRefGoogle Scholar
Hamm, H. A., Lokale topologische Eigenschaften komplexer Räume , Math. Ann. 191 (1971), 235–252.CrossRefGoogle Scholar
Hamm, H. A. and Lê, D. T., Un théorème de Zariski du type de Lefschetz , Ann. Sci. Éc. Norm. Supér. (4) 6 (1973), 317–355.CrossRefGoogle Scholar
Kouchnirenko, A. G., Polyèdres de Newton et nombres de Milnor , Invent. Math. 32 (1976), 1–31.CrossRefGoogle Scholar
Milnor, J., Singular Points of Complex Hypersurfaces, Ann. of Math. Stud. 61, Princeton Univ. Press, Princeton, NJ; Univ. Tokyo Press, Tokyo, 1968.Google Scholar
Oka, M., On the bifurcation of the multiplicity and topology of the Newton boundary , J. Math. Soc. Japan 31 (1979), 435–450.CrossRefGoogle Scholar
Oka, M., On the topology of the Newton boundary II (generic weighted homogeneous singularity) , J. Math. Soc. Japan 32 (1980), 65–92.CrossRefGoogle Scholar
Oka, M., On the topology of the Newton boundary III , J. Math. Soc. Japan 34 (1982), 541–549.CrossRefGoogle Scholar
Oka, M., Non-Degenerate Complete Intersection Singularity, Actualités Math., Hermann, Paris, 1997.Google Scholar
Remmert, R., Holomorphe und meromorphe Abbildungen komplexer Räume , Math. Ann. 133 (1957), 328–370.CrossRefGoogle Scholar
Whitney, H., Tangents to an analytic variety , Ann. of Math. (2) 81 (1965), 496–549.CrossRefGoogle Scholar