Article contents
On differential polynomials, II
Published online by Cambridge University Press: 22 January 2016
Abstract
In Part II, we shall be concerned with applications of classical invariant theory, to statistic physics and to theta functions. Main theorem in Chapter 2 is stated as follows:
For a partition function
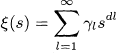
satisfying γl ≥ 0 (l ≥ 1) and α > 0, the 2n-apolar of ξ(s)

has the expansion
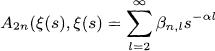
such that βn,1 ≥ 0 (l ≥ 2). This means, for a given partition function ξ(s) with nonnegative relative probabilities, we construct a sequence of partition functions A2n (ξ(s), ξ(s))n≥1 with the same properties, which may be considered a sequence of symbolical higher derivative of ξ(s). The main theorem in Chapter 3 is stated as follows: For given theta functions φ1(z) and φ2(z) of level n1 and n2 respectively, in g variables z = (z1, z2,…, zg), then r = (r1, r2,…, rg-apolar
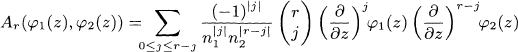
is a theta function of level n1 + n2, and
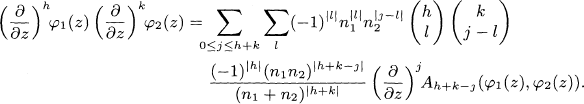
- Type
- Research Article
- Information
- Copyright
- Copyright © Editorial Board of Nagoya Mathematical Journal 1997
References
- 2
- Cited by




