Hostname: page-component-848d4c4894-4rdrl Total loading time: 0 Render date: 2024-06-23T09:55:25.187Z Has data issue: false hasContentIssue false
  • English
  • Français

Mixed periodic Jacobi continued fractions

Published online by Cambridge University Press:  22 January 2016

Yoshifumi Kato
Yoshifumi Kato*
Affiliation:
Department of Engineering Mathematics, Faculty of Engineering, Nagoya University, Chikusa-ku, Nagoya, 464, JAPAN
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let b0 be a positive real number and

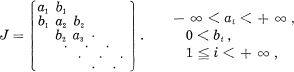
be a Jacobi matrix. We can associate with them a Jacobi continued fraction, which will be abbreviated to a J fraction from the next section, as follows

where An(z)/Bn(z) is the n-th Padé approximant of φ(z).

Type
Research Article
Information
Nagoya Mathematical Journal , Volume 104 , December 1986 , pp. 129 - 148
Copyright
Copyright © Editorial Board of Nagoya Mathematical Journal 1986

References

[ 1 ] Jones, W. B.and Thron, W. J., Continued Fractions, Addison-Wesley, 1980.Google Scholar
[ 2 ] Kato, Y., On the spectral density of periodic Jacobi matrices, Proceedings of RIMS Symposium on Non-Linear Integrable Systems-Classical Theory and Quantum Theory, Kyoto Japan, 1981, 153–181, World Science Publishing Co., 1983.Google Scholar
[ 3 ] Kato, Y., Periodic Jacobi continued fractions, International Symposium on Orthogonal Polynomials and their Applications, Bar-le-Duc France, 1984, Springer Lecture Notes in Math.Google Scholar
[ 4 ] Lambin, Ph. and Gaspard, J.-P., Continued fraction technique for tight-binding systems, A generalized-moments method, Phys. Rev. B., 26 (1982), 4356–4368.Google Scholar
[ 5 ] Magnus, A., Recurrence coefficients for orthogonal polynomials on connected and non connected sets, Springer Lecture Notes in Math., 765 (1979), 150–171.Google Scholar
[ 6 ] van Moerbeke, P., The spectrum of Jacobi matrices, Invent. Math., 37 (1976), 45–81.Google Scholar
[ 7 ] van Moerbeke, P., and Mumford, D., The spectrum of difference operators and algebraic curves, Acta Math., 143 (1979), 93–154.Google Scholar
[ 8 ] Moser, J., Finitely many mass points on the line under the influence of an exponential potential—an integrable system, in Battelle Recontres Summer Lectures, Springer Lecture Notes in Phys., 1974, 467–497.Google Scholar
[ 9 ] Nuttall, J. and Singh, S. R., Orthogonal polynomials and Padé approximants associated with a system of arcs, J. Approx. Theory, 21 (1977), 1–42.Google Scholar
[10] Szegö, G., Orthogonal Polynomials, A.M.S. Colloq. XXIII, 1939.Google Scholar
[11] Turchi, P., Ducastelle, F. and Treglia, G., Band gaps and asymptotic behaviour of continued fraction coefficients, J. Phys. C., 15 (1982), 2891–2924.Google Scholar
[12] Woess, W., Random walks and periodic continued fractions, preprint, 1984, to appear in Adv. in Appl. Probab.CrossRefGoogle Scholar