Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Kojo, Katsuya
1993.
$S\alpha S\;M(t)$-processes and their canonical representations.
Hiroshima Mathematical Journal,
Vol. 23,
Issue. 2,
Kokoszka, Piotr S.
and
Taqqu, Murad S.
1993.
Asymptotic dependence of moving average type self-similar stable random Fields.
Nagoya Mathematical Journal,
Vol. 130,
Issue. ,
p.
85.
Takenaka, Shigeo
1993.
Stochastic Processes.
p.
303.
Kokoszka, Piotr S.
and
Taqqu, Murad S.
1994.
New classes of self-similar symmetric stable random fields.
Journal of Theoretical Probability,
Vol. 7,
Issue. 3,
p.
527.
Kokoszka, Piotr S.
and
Taqqu, Murad S.
1995.
Fractional ARIMA with stable innovations.
Stochastic Processes and their Applications,
Vol. 60,
Issue. 1,
p.
19.
MORI, Toshio
and
SATO, Yumiko
1996.
Construction and asymptotic behavior of a class of self-similar stable processes.
Japanese journal of mathematics. New series,
Vol. 22,
Issue. 2,
p.
275.
Pipiras, Vladas
and
Taqqu, Murad S.
2002.
The structure of self-similar stable mixed moving averages.
The Annals of Probability,
Vol. 30,
Issue. 2,
Huang, Zhi-yuan
and
Li, Chu-jin
2005.
Anisotropic Fractional Brownian Random Fields as White Noise Functionals.
Acta Mathematicae Applicatae Sinica, English Series,
Vol. 21,
Issue. 4,
p.
655.
Istas, Jacques
2006.
On Fractional Fields indexed by Metric Spaces.
Electronic Communications in Probability,
Vol. 11,
Issue. none,
Estrade, Anne
and
Istas, Jacques
2010.
Ball throwing on spheres.
Bernoulli,
Vol. 16,
Issue. 4,
Biermé, Hermine
Estrade, Anne
and
Kaj, Ingemar
2010.
Self-similar Random Fields and Rescaled Random Balls Models.
Journal of Theoretical Probability,
Vol. 23,
Issue. 4,
p.
1110.
Istas, Jacques
2012.
Estimating self-similarity through complex variations.
Electronic Journal of Statistics,
Vol. 6,
Issue. none,
Biermé, Hermine
Demichel, Yann
and
Estrade, Anne
2013.
Fractional Poisson field and fractional Brownian field: why are
they resembling but different?.
Electronic Communications in Probability,
Vol. 18,
Issue. none,
Jung, Paul
2014.
Random-Time Isotropic Fractional Stable Fields.
Journal of Theoretical Probability,
Vol. 27,
Issue. 2,
p.
618.
Dang, Thi To Nhu
and
Istas, Jacques
2017.
Estimation of the Hurst and the stability indices of a $H$-self-similar stable process.
Electronic Journal of Statistics,
Vol. 11,
Issue. 2,
Pipiras, Vladas
and
Taqqu, Murad S.
2017.
Stable Non-Gaussian Self-Similar Processes with Stationary Increments.
p.
49.
Fu, Zuopeng
and
Wang, Yizao
2020.
Stable Processes with Stationary Increments Parameterized by Metric Spaces.
Journal of Theoretical Probability,
Vol. 33,
Issue. 3,
p.
1737.
Basse-O’Connor, Andreas
Pilipauskaitė, Vytautė
and
Podolskij, Mark
2021.
Power variations for fractional type infinitely divisible random fields.
Electronic Journal of Probability,
Vol. 26,
Issue. none,
Pilipauskait˙e, Vytaut˙e
and
Surgailis, Donatas
2022.
Local scaling limits of Lévy driven fractional random fields.
Bernoulli,
Vol. 28,
Issue. 4,
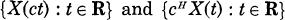 are subject to the same law (see [10]).
are subject to the same law (see [10]).



