Hostname: page-component-76fb5796d-45l2p Total loading time: 0 Render date: 2024-04-25T09:30:54.338Z Has data issue: false hasContentIssue false
  • English
  • Français

HYPERBOLIC 3-MANIFOLDS AND CLUSTER ALGEBRAS

Part of: Arithmetic rings and other special rings Low-dimensional topology

Published online by Cambridge University Press:  28 September 2017

KENTARO NAGAO ,
YUJI TERASHIMA  and
MASAHITO YAMAZAKI
KENTARO NAGAO
Affiliation:
Graduate School of Mathematics, Nagoya University, Japan email kentaron@math.nagoya-u.ac.jp
YUJI TERASHIMA
Affiliation:
Department of Mathematical and Computing Sciences, Tokyo Institute of Technology, Japan email tera@is.titech.ac.jp
MASAHITO YAMAZAKI
Affiliation:
Kavli Institute for the Physics and Mathematics of the Universe, University of Tokyo, Japan email masahito.yamazaki@ipmu.jp
Get access Rights & Permissions [Opens in a new window]

Abstract

We advocate the use of cluster algebras and their 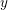$y$-variables in the study of hyperbolic 3-manifolds. We study hyperbolic structures on the mapping tori of pseudo-Anosov mapping classes of punctured surfaces, and show that cluster 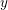$y$-variables naturally give the solutions of the edge-gluing conditions of ideal tetrahedra. We also comment on the completeness of hyperbolic structures.

MSC classification

Primary: 13F60: Cluster algebras
Secondary: 57M27: Invariants of knots and 3-manifolds
Type
Article
Information
Nagoya Mathematical Journal , Volume 235 , September 2019 , pp. 1 - 25
Copyright
© 2017 Foundation Nagoya Mathematical Journal  

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Andriyash, E., Denef, F., Jafferis, D. L. and Moore, G. W., Wall-crossing from supersymmetric galaxies , J. High Energy Phys. 01 (2012), 115, arXiv:1008.0030.10.1007/JHEP01(2012)115Google Scholar
Agol, I., “ Ideal triangulations of pseudo-Anosov mapping tori ”, in Topology and Geometry in Dimension Three, Contemporary Mathematics 560 , American Mathematical Society, Providence, RI, 2011, 1–17.Google Scholar
Alday, L. F., Gaiotto, D. and Tachikawa, Y., Liouville correlation functions from four-dimensional gauge theories , Lett. Math. Phys. 91 (2010), 167–197.Google Scholar
Amiot, C., Cluster categories for algebras of global dimension 2 and quivers with potential , Ann. Inst. Fourier 59(6) (2009), 2525–2590.10.5802/aif.2499Google Scholar
Bernstein, A., Fomin, S. and Zelevinsky, A., Cluster algebras III: upper bounds and double Bruhat cells , Duke Math. J. 126 (2005), 1–52.Google Scholar
Culler, M., Dunfield, N. M. and Weeks, J. R., Snappy, a computer program for studying the geometry and topology of 3-manifolds, http://snappy.computop.org.Google Scholar
Cecotti, S., Neitzke, A. and Vafa, C., $R$ -twisting and $4d/2d$ correspondences, preprint, arXiv:1006.3435.Google Scholar
Dupont, J. L. and Sah, C.-H., Dilogarithm identities in conformal field theory and group homology , Comm. Math. Phys. 161(2) (1994), 265–282.Google Scholar
Eager, R. and Franco, S., Colored BPS pyramid partition functions, quivers and cluster transformations , J. High Energy Phys. 09 (2012), 038, arXiv:1112.1132.10.1007/JHEP09(2012)038Google Scholar
Fock, V. and Goncharov, A., Moduli spaces of local systems and higher Teichmüller theory , Publ. Math. Inst. Hautes Études Sci. 103(1) (2006), 1–211.10.1007/s10240-006-0039-4Google Scholar
Fock, V. and Goncharov, A., “ Dual Teichmüller and lamination spaces ”, in Handbook of Teichmüller Theory, Vol. I, no. 1, Eur. Math. Soc., Zurich, 2007, 647–684.10.4171/029-1/16Google Scholar
Fock, V. V. and Goncharov, A. B., The quantum dilogarithm and representations of quantum cluster varieties , Invent. Math. 175(2) (2009), 223–286.Google Scholar
Fomin, S., “ Total positivity and cluster algebras ”, in Proceedings of the International Congress of Mathematicians, Vol. II, Hindustan Book Agency, New Delhi, 2010, 125–145.Google Scholar
Fomin, S., Shapiro, M. and Thurston, D., Cluster algebras and triangulated surfaces. Part I: cluster complexes , Acta Math. 201(1) (2008), 83–146.10.1007/s11511-008-0030-7Google Scholar
Fomin, S. and Zelevinsky, A., Cluster algebras I: foundations , J. Amer. Math. Soc. 15(2) (2002), 497–529.10.1090/S0894-0347-01-00385-XGoogle Scholar
Fomin, S. and Zelevinsky, A., Y-systems and generalized associahedra , Ann. of Math. (2) 158(3) (2003), 977–1018.Google Scholar
Gaiotto, D., Moore, G. W. and Neitzke, A., Framed BPS states , Adv. Theor. Math. Phys. 17(2) (2013), 241–397.10.4310/ATMP.2013.v17.n2.a1Google Scholar
Gekhtman, M., Shapiro, M. Z. and Vainshtein, A. D., Cluster algebras and poisson geometry , Mosc. Math. J. 3 (2003), 899–934.10.17323/1609-4514-2003-3-3-899-934Google Scholar
Gliozzi, F. and Tateo, R., Thermodynamic Bethe ansatz and three-fold triangulations , Internat. J. Modern Phys. A 11(22) (1996), 4051–4064.10.1142/S0217751X96001905Google Scholar
Guéritaud, F., On canonical triangulations of once-punctured torus bundles and two-bridge link complements , Geom. Topol. 10 (2006), 1239–1284.Google Scholar
Kedem, R., Q-systems as cluster algebras , J. Phys. A 41 (2008), 194011.10.1088/1751-8113/41/19/194011Google Scholar
Keller, B., “ Cluster algebras, quiver representations and triangulated categories ”, in Triangulated Categories, London Mathematical Society Lecture Note Series 375 , Cambridge University Press, Cambridge, 2010, 76–160.10.1017/CBO9781139107075.004Google Scholar
Keller, B., “ On cluster theory and quantum dilogarithm identities ”, in Representations of Algebras and Related Topics, EMS Ser. Congr. Rep., Eur. Math. Soc., Zürich, 2011, 85–116.10.4171/101-1/3Google Scholar
Keller, B., The periodicity conjecture for pairs of Dynkin diagrams , Ann. of Math. (2) 177(1) (2013), 111–170.Google Scholar
Kimura, Y., Quantum unipotent subgroup and dual canonical basis , Kyoto J. Math. 52(2) (2012), 277–331.Google Scholar
Kashaev, R. and Nakanishi, T., Classical and quantum dilogarithm identities , SIGMA 7(102) (2011), 29, arXiv:1104.4630.Google Scholar
Kuniba, A., Nakanishi, T. and Suzuki, J., T-systems and Y-systems in integrable systems , J. Phys. A 44 (2011), 103001.10.1088/1751-8113/44/10/103001Google Scholar
Kontsevich, M. and Soibelman, Y., Stability structures, motivic Donaldson–Thomas invariants and cluster transformations, preprint, arXiv:0811.2435.Google Scholar
Kitayama, T. and Terashima, Y., Torsion functions on moduli spaces in view of the cluster algebra , Geom. Dedicata 175 (2015), 125–143.10.1007/s10711-014-0032-xGoogle Scholar
Keller, B. and Yang, D., Derived equivalences from mutations of quivers with potential , Adv. Math. 226(3) (2011), 2118–2168.Google Scholar
Leclerc, B., “ Cluster algebras and representation theory ”, in Proceedings of the International Congress of Mathematicians, Vol. IV, Hindustan Book Agency, New Delhi, 2010, 2471–2488.Google Scholar
Nagao, K., Mapping class group, Donaldson–Thomas theory and $S$ -duality, http://www.math.nagoya-u.ac.jp/∼kentaron/MCG_DT.pdf.Google Scholar
Nagao, K., Quantum dilogarithm idetities , RIMS Kokyuroku Bessatsu B28 (2011), 165–170.Google Scholar
Nagao, K., Donaldson–Thomas theory and cluster algebras , Duke Math. J. 162(7) (2013), 1313–1367.Google Scholar
Nakajima, H., Quiver varieties and cluster algebras , Kyoto J. Math. 51(1) (2011), 71–126.10.1215/0023608X-2010-021Google Scholar
Nakanishi, T., Dilogarithm identities for conformal field theories and cluster algebras: simply laced case , Nagoya Math. J. 202 (2011), 23–43.Google Scholar
Nakanishi, T., “ Periodicities in cluster algebras and dilogarithm identities ”, in Representations of Algebras and Related Topics, EMS Ser. Congr. Rep., Eur. Math. Soc., Zürich, 2011, 407–443.10.4171/101-1/9Google Scholar
Neumann, W. D., “ Combinatorics of triangulations and the Chern–Simons invariant for hyperbolic 3-manifolds ”, in Topology ’90 (Columbus, OH, 1990), Ohio State Univ. Math. Res. Inst. Publ. 1 , de Gruyter, Berlin, 1992, 243–271.Google Scholar
Nahm, W., Recknagel, A. and Terhoeven, M., Dilogarithm identities in conformal field theory , Modern Phys. Lett. A 8(19) (1993), 1835–1847.Google Scholar
Neumann, W. D. and Zagier, D., Volumes of hyperbolic 3-manifolds , Topology 24 (1985), 307–332.10.1016/0040-9383(85)90004-7Google Scholar
Plamondon, P.-G., Cluster characters for cluster categories with infinite-dimensional morphism spaces , Adv. Math. 227(1) (2011), 1–39.10.1016/j.aim.2010.12.010Google Scholar
Teschner, J., Quantization of the Hitchin moduli spaces, Liouville theory, and the geometric Langlands correspondence I , Adv. Theor. Math. Phys. 15(2) (2011), 471–564.10.4310/ATMP.2011.v15.n2.a6Google Scholar
Teschner, J., “ An analog of a modular functor from quantized Teichmüller theory ”, in Handbook of Teichmüller Theory, Vol. I, no. 1, Eur. Math. Soc., Zurich, 2007, 685–760.10.4171/029-1/17Google Scholar
Thurston, W. P., The geometry and topology of three-manifolds, 1978–1979.Google Scholar
Terashima, Y. and Yamazaki, M., SL(2, R) Chern–Simons, Liouville, and Gauge theory on duality walls , J. High Energy Phys. 1108 (2011), 135, arXiv:1103.5748.10.1007/JHEP08(2011)135Google Scholar
Terashima, Y. and Yamazaki, M., Semiclassical analysis of the 3d/3d relation , Phys. Rev. D88(2) (2013), 026011.Google Scholar
Terashima, Y. and Yamazaki, M., 3d N = 2 theories from cluster algebras , Progr. Theoret. Exp. Phys. 023 (2014), B01.Google Scholar