Article contents
The decay of the local energy for wave equations with discontinuous coefficients
Published online by Cambridge University Press: 22 January 2016
Extract
The exponential decay of the local energy for wave equations in exterior domains of the odd dimensional space has been proved in [1] ~ [6] etc. under the Dirichlet boundary condition and in [5], [7] under the Neumann condition and the other conditions. In this paper, we shall consider this problem for the following equation:
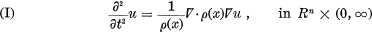
- Type
- Research Article
- Information
- Copyright
- Copyright © Editorial Board of Nagoya Mathematical Journal 1977
References
- 2
- Cited by




