Hostname: page-component-5c6d5d7d68-vt8vv Total loading time: 0.001 Render date: 2024-08-15T20:00:22.265Z Has data issue: false hasContentIssue false
  • English
  • Français

Circle Means of Green’s Functions

Published online by Cambridge University Press:  22 January 2016

Mitsuru Nakai
Mitsuru Nakai*
Affiliation:
Nagoya University
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Consider the polar coordinate differentials (dr, dθ) on a hyperbolic Riemann surface R with center z0 ∈ R which are given by

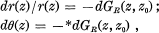
where GR(z, ζ) is the Green’s function on R with pole ζ ∈ R.

Type
Research Article
Information
Nagoya Mathematical Journal , Volume 49 , March 1973 , pp. 1 - 7
Copyright
Copyright © Editorial Board of Nagoya Mathematical Journal 1973

References

[1] Brelot, M.-Choquet, G.: Espaces et lignes de Green, Ann. Inst. Fourier 3 (1951), 199–263.Google Scholar
[2] Kuramochi, Z.: Harmonic measures and capacity of sets of the ideal boundary. II, Proc. Japan Acad., 32 (1955), 25–30.Google Scholar
[3] Kusunoki—, Y. Mori, S.: On the harmonic boundary of an open Riemann surface, Japan. J. Math., 24 (1960), 52–56.Google Scholar
[4] Nakai, M.: Bordered Riemann surface with parabolic double, Proc. Japan Acad., 37 (1961), 553–555.Google Scholar
[5] Nakai, M.: Behaviour of Green lines at Royden’s boundary of Riemann surfaces, Nagoya Math. J., 24 (1964), 1–27.Google Scholar
[6] Sario—, L. Nakai, M.: Classification Theory of Riemann Surfaces, Springer, 1970.Google Scholar