Hostname: page-component-6d856f89d9-gndc8 Total loading time: 0 Render date: 2024-07-16T07:37:16.011Z Has data issue: false hasContentIssue false
  • English
  • Français

Boundary behaviour of extremal plurisubharmonic functions

Published online by Cambridge University Press:  22 January 2016

Stanley M. Einstein-Matthews
Stanley M. Einstein-Matthews*
Affiliation:
Uppsala University, Department of Mathematics, P. O. Box 480 S-751 06 Uppsala, Sweden. E-mail: smem@math.uu.se
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In [Mo.l], S. Momm studied the boundary behaviour of extremal plurisubharmonic functions by using the pluricomplex Green function gΩ of a bounded convex domain Ω in Cn to exhaust the domain by a family of sublevel sets. Let Ω be a bounded convex domain in Cn containing the origin in its interior. The pluricomplex green function of Ω with a pole 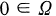is defined by

(1.1)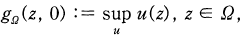

Type
Research Article
Information
Nagoya Mathematical Journal , Volume 138 , June 1995 , pp. 65 - 112
Copyright
Copyright © Editorial Board of Nagoya Mathematical Journal 1995

References

[A-P-S.l] Andersson, M., Passare, M. and Sigurdsson, R., Analytic Functionals and Complex Convexity, Manuscript., Department of Mathematics, Stockholms University, 1991.Google Scholar
[B.l] Bedford, E., Survey of Pluri-potential Theory, Proceedings of the Mittag Leffler Institute 1987–88, Fornaess, J.-E., editor, Princeton University Press. 1993.Google Scholar
[B-De.1] Bedford, B. and Demailly, J.-P., Two counter example concerning the pluricomplex Green function in Cn , Indiana U. Math. J., 37 (1988), 865–867.Google Scholar
[B-K.1] Bedford, B. and Kalka, M., Foliations and complex Monge-Ampère equations, Comm. on Pure and Applied Math., 30 (1977), 543–571.Google Scholar
[Be-Po.1] Behnke, B. and Peschl, E., Zur theorie der Funktionen mehrerer komplexer Varãnderlichen. Konvexitát in bezug auf analytische Ebenen im kleinen undgrossen, Math. Ann., 111 (1935), 158–177.Google Scholar
[B-T.1] Bedford, and Taylor, B. A., The Dirichlet Problem for a Complex Monge-Ampère Equation, Invent. Math., 37 (1976), 1–44.Google Scholar
[B-T.2] Bedford, and Taylor, B. A., A new capacity for plurisubharmonic functions, Acta Math., 149 (1982), 1–40.Google Scholar
[B-T.3] Bedford, and Taylor, B. A., Plurisubharmonic functions with logarithmic singularities, Ann. Inst. Fourier, Grenoble, 38 (1988), 133–171.Google Scholar
[C-L-N.1] Chern, S. S., Levine, H. I., Nirenberg, L., Intrinsic norms on a complex manifold, Global Analysis (papers in honour of Kodaira, K.) University of Tokyo Press; Tokyo 1969, 119–139.Google Scholar
[De.1] Demailly, J-P., Mesures de Monge-Ampère et mesures pluriharmoniques, Math. Z., 194 (1987), 519–564.Google Scholar
[De.2] Demailly, J-P., Monge-Ampère Operators, Lelong Numbers and Intersection Theory. Prépublication de l’Institut Fourier. Grenoble, 1991.Google Scholar
[De.3] Demailly, J-P., Nombres de Lelong généralisés, théorèmes d’intégralité et d’analyticité, Acta Math., 159 (1987), 153–169.CrossRefGoogle Scholar
[E-M.l] Einstein-Matthews, S. M., Transformations of solutions of the complex Monge-Ampère equation, Manuscript., Mathematics Department, Uppsala University.Google Scholar
[E-M.2] Einstein-Matthews, S. M., Extremal Plurisubharmonic Functions and Complex Monge-Ampère Operators. Ph. D. Thesis 1993. Uppsala University.Google Scholar
[Höi.] Hörmander, L., Convexities, Lectures 1991–1992, Lund, Mathematics Department, Manuscript, 1992.Google Scholar
[Ki.1] Kiselman, C. O., The partial Legendre transformation for plurisubharmonic functions, Invent Math., 49 (1978),137–148.Google Scholar
[Ki.2] Kiselman, C. O., Densité des fonctions plurisousharmoniques, Bull. Soc. Math. France 107 (1979), 295–304.Google Scholar
[Ki.3] Kiselman, C. O., Duality of functions defined in linearly convex sets, Preprint. Mathematics, Department, Uppasala Univ. January 18, 1993.Google Scholar
[Ki.4] Kiselman, C. O., Attenuating the singularities of plurisubharmunic functions, Preprint, Mathematics Department, Uppsala University, 1993.Google Scholar
[Kl.1] Klimek, M., Pluripotential Theory Oxford Science Publications, 1991.Google Scholar
[K1.2] Klimek, M., Extremal plurisubharmonic functions and invariant pseudodistances, Bulletin de la Société Mathématique de France, 113 (1985), 231–240.Google Scholar
[Kz.1] Kruzhilin, N. G., Foliations connected with Monge-Ampère equations in Hartogs domains, Izv. Akad. Nauk. SSSR, 48 (1984), 1109–1118.Google Scholar
[Le.1] Lelong, P., Fonction de Green pluricomplexe et lemmes de Schwartz dans les espaces de Banach, J. Math. Pures et Appl., 68 (1989), 319–347.Google Scholar
[Lem.1] Lempert, L., La métrique de Kobayashi et la représentation de domaines sur la boule, Bull. Soc. Math. France, 109 (1991), 427–474.Google Scholar
[Lem.2] Lempert, L., Symmetries and other transformations of the Complex Monge-Ampère equation. Duke Math. J. 52(4) (1985), 869–885.Google Scholar
[Lem.3] Lempert, L., Solving the degenerate complex Monge-Ampère equation with one con centrated singularity, Math. Ann., 263 (1983), 515–532.Google Scholar
[Lem.4] Lempert, L., Intrinsic distances and holomorphic retracts, Proc. Conf. Varna, 1981; Compi. Anal, and Appl., Sofia (1984), 341–364.Google Scholar
[Lem.5] Lempert, L., Holomorphic invariants, normal forms, and the moduli space of convex domains, Annals of Math. 128 (1988), 43–78.Google Scholar
[Lem.6] Lempert, L., Holomorphic retracts and intrinsic metrics in convex domains, Analy sis Math., 8 (1982), 257–261.Google Scholar
[Lem.7] Lempert, L., On three-diemensional Cauchy-Riemann manifolds, J. Amer. Math. Soc, 5(4) (1992), 923–969.Google Scholar
[Ma.1] Martineau, A., Sur la notion d’ensembles fortement linéellement convexe, Anais Acad. Brasil Ciênc, 40 (1968), 427–435.Google Scholar
[Mo.1] Momm, S., Boundary Behavior of Extremal Plurisubharmonic Functions. Manuscript. Universitãt Duesseldorf, Germany, 1992.Google Scholar
[Pa.1] Patrizio, G., Parabolic exhaustions for strictly convex domains, Manuscr. Math., 47 (1984), 271–309.CrossRefGoogle Scholar
[Po-Sh.1] Poletsky, E. A. and Shabat, B. V., Invariant metrics, Encyclopaedia of Mathematics Vol. 9. Several complex variables III. ed. Khenkin, G. M., 63–111, Springer, Berlin, 1989.Google Scholar
[Sd.1] Sadullaev, A., Plurisubharmonic measures and capacities on complex manifolds, Russian Math. Surveys, 36 (1989), 61–119.Google Scholar
[Sib.1] Sibony, N., Quelques problemes de prolongement de courants en analyse complexe, Duke Math. J., 52 (1985), 157–197.Google Scholar
[Si.1] Siciak, J., Extremal plurisubharmonic functions in C, Ann. Polon. Math., 319 (1981), 175–211.Google Scholar
[Si.2] Siciak, J., Extremal plurisubharmonic Functions and Capacities in Cn , Sophia Kokyuroko in Mathematics 14, Sofia University, Tokyo, Japan, 1982.Google Scholar
[Siu.l] Siu, Y.-T., Analyticity of sets associated to Lelong numbers and the extension of closed positive currents, Invent. Math., 27 (1974), 53 — 156.Google Scholar
[Za.l] Zaharyuta, V. P., Spaces of analytic functions and maximal plurisubharmonic functions, Doctoral dissertation. Rostov-on-Don. 1–281 (Russian), 1984.Google Scholar
[Za.2] Zaharyuta, V. P., Spaces of analytic functions, Survey, 1–95 (Russian).Google Scholar