Hostname: page-component-848d4c4894-v5vhk Total loading time: 0 Render date: 2024-06-24T09:48:54.571Z Has data issue: false hasContentIssue false
  • English
  • Français

Addendum to the Paper “A note on Weighted bergman Spaces and the cesaro operator”

Published online by Cambridge University Press:  11 January 2016

Der-Chen Chang  and
Stevo Stević
Der-Chen Chang
Affiliation:
Department of Mathematics Georgetown UniversityWashington D.C., 20057USAchang@georgetown.edu
Stevo Stević
Affiliation:
Mathematical Institute of Serbian Academy of Science Knez Mihailova35/I 11000Beograd Serbiasstevic@ptt.yu; sstevo@matf.bg.ac.yu
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

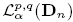Let H(Dn) be the space of holomorphic functions on the unit polydisk Dn, and let , where p, q> 0, α = (α1,…,αn) with αj > -1, j =1,..., n, be the class of all measurable functions f defined on Dn such that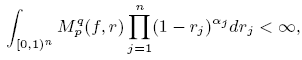

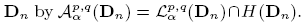where Mp(f,r) denote the p-integral means of the function f. Denote the weighted Bergman space on . We provide a characterization for a function f being in 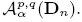. Using the characterization we prove the following result: Let p> 1, then the Cesàro operator is bounded on the space .

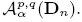Keywords

47B3846E15
Type
Research Article
Information
Nagoya Mathematical Journal , Volume 180 , 2005 , pp. 77 - 90
Copyright
Copyright © Editorial Board of Nagoya Mathematical Journal 2005

References

[1] Benke, G. and Chang, D. C., A note on weighted Bergman spaces and the Cesáro operator, Nagoya Math. J., 159 (2000), 25–43.Google Scholar
[2] Siskakis, A., Weighted integrals of analytic functions, Acta Sci. Math., 66 (2000), 651–664.Google Scholar
[3] Stević, S., Weighted integrals of holomorphic functions in Cn , Complex Variables, 47 (9) (2002), 821–838.Google Scholar
[4] Stević, S., Weighted integrals of harmonic functions, Studia Sci. Math. Hung., 39 (1-2) (2002), 87–96.Google Scholar
[5] Stević, S., Cesàro averaging operators, Math. Nachr., 248-249 (2003), 185–189.Google Scholar
[6] Stević, S., Weighted integrals and conjugate functions in the unit disk, Acta Sci. Math., 69 (2003), 109–119.Google Scholar
[7] Stević, S., On generalized weighted Bergman spaces, Complex Variables, 49 (2) (2004), 109–124.Google Scholar
[8] Stević, S., Weighted integrals for polyharmonic type functions, Houston J. Math., 30 (2) (2004), 511–521.Google Scholar