Hostname: page-component-8448b6f56d-tj2md Total loading time: 0 Render date: 2024-04-25T02:04:57.299Z Has data issue: false hasContentIssue false
  • English
  • Français

Third-Generation TB-LMTO

Published online by Cambridge University Press:  10 February 2011

O. K. Andersen ,
C. Arcangeli ,
R. W. Tank ,
T. Saha-Dasgupta ,
G. Krier ,
O. Jepsen  and
I. Dasgupta
O. K. Andersen
Affiliation:
Max-Planck Institut für Festkörperforschung, Stuttgart, Germany
C. Arcangeli
Affiliation:
Max-Planck Institut für Festkörperforschung, Stuttgart, Germany
R. W. Tank
Affiliation:
Max-Planck Institut für Festkörperforschung, Stuttgart, Germany
T. Saha-Dasgupta
Affiliation:
Max-Planck Institut für Festkörperforschung, Stuttgart, Germany
G. Krier
Affiliation:
Max-Planck Institut für Festkörperforschung, Stuttgart, Germany
O. Jepsen
Affiliation:
Max-Planck Institut für Festkörperforschung, Stuttgart, Germany
I. Dasgupta
Affiliation:
Max-Planck Institut für Festkörperforschung, Stuttgart, Germany
Get access

Abstract

We describe the screened Korringa-Kohn-Rostoker (KKR) method and the third-generation linear muffin-tin orbital (LMTO) method for solving the single-particle Schrödinger equation for a MT potential. In the screened KKR method, the eigenvectors CRL,i are given as the non-zero solutions, and the energies εi as those for which such solutions can be found, of the linear homogeneous equations: 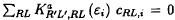, where Ka (ε) is the screened KKR matrix. The screening is specified by the boundary condition that, when a screened spherical wave 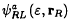is expanded in spherical harmonics YR′L′ (ȓR′) about its neighboring sites R′, then each component either vanishes at a radius, rR′=aR′L′, or is a regular solution at that site. When the corresponding “hard” spheres are chosen to be nearly touching, then the KKR matrix is usually short ranged and its energy dependence smooth over a range of order 1 Ry around the centre of the valence band. The KKR matrix, K (εν), at a fixed, arbitrary energy turns out to be the negative of the Hamiltonian, and its first energy derivative, K (εν), to be the overlap matrix in a basis of kinked partial waves, φRL (εν, rR), each of which is a partial wave inside the MT-sphere, tailed with a screened spherical wave in the interstitial, or taking the other point of view, a screened spherical wave in the interstitial, augmented by a partial wave inside the sphere. When of short range, K (ε) has the two-centre tight-binding (TB) form and can be generated in real space, simply by inversion of a positive definite matrix for a cluster. The LMTOs, χRL (εν), are smooth orbitals constructed from φRL(εν, rR) and φRL(εν, rR), and the Hamiltonian and overlap matrices in the basis of LMTOs are expressed solely in terms of K (εν) and its first three energy derivatives. The errors of the single-particle energies εi obtained from the Hamiltonian and overlap matrices in the φ(εν)- and χ(εν) bases are respectively of second and fourth order in εi – εi. Third-generation LMTO sets give wave functions which are correct to order εi – εν, not only inside the MT spheres, but also in the interstitial region. As a consequence, the simple and popular formalism which previously resulted from the atomic-spheres approximation (ASA) now holds in general, that is, it includes downfolding and the combined correction. Downfolding to few-orbital, possibly short-ranged, low-energy, and possibly orthonormal Hamiltonians now works exceedingly well, as is demonstrated for a high-temperature superconductor. First-principles sp3 and sp3d5 TB Hamiltonians for the valence and lowest conduction bands of silicon are derived. Finally, we prove that the new method treats overlap of the potential wells correctly to leading order and we demonstrate how this can be exploited to get rid of the empty spheres in the diamond structure.

Type
Research Article
Information
MRS Online Proceedings Library (OPL) , Volume 491: Symposium R – Tight Binding Approach to Computational Materials Science , 1997 , 3
Copyright
Copyright © Materials Research Society 1998

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

1 Korringa, M., Physica 13, 392 (1947);Google Scholar
Kohn, W. and Rostoker, J., Phys. Rev. 94, 1111 (1954).Google Scholar
2 Andersen, O.K., Postnikov, A.V., and Savrasov, S. Yu., in Applications of Multiple Scattering Theory to Materials Science, eds. Butler, W.H., Dederichs, P.H., Gonis, A., and Weaver, R.L., MRS Symposia Proceedings No. 253 (Materials Research Society, Pittsburgh, 1992) p 37.Google Scholar
3 Andersen, O.K., Jepsen, O., and Krier, G. in Lectures on Methods of Electronic Structure Calculations, edited by Kumar, V., Andersen, O.K., and Mookerjee, A. (World Scientific Publishing Co., Singapore, 1994), pp. 63–124.Google Scholar
4 Zeller, R., Dederichs, P.H., Ujfalussy, B., Szunyogh, L., and Weinberger, P., Phys. Rev. B 52, 8807 (1995).Google Scholar
5 Andersen, O.K., Solid State Commun. 13, 133 (1973);Google Scholar
Andersen, O.K., Phys. Rev. B 12, 3060 (1975);Google Scholar
Jepsen, O., Andersen, O.K., and Mackintosh, A.R., Phys. Rev. 12, 3084 (1975).Google Scholar
6 Andersen, O.K. and Jepsen, O., Phys. Rev. Lett. 53, 2571 (1984).Google Scholar
7 Skriver, H.L., The LMTO Method (Springer-Verlag, Berlin, 1984).Google Scholar
8 Skriver, H.L. and Rosengaard, N.M., Phys. Rev. B 43, 9538 (1991);Google Scholar
Turek, I., Drchal, V., Kudrnovsky, J., Sob, M., and Weinberger, P., Electronic Structure of Disordered Alloys, Surfaces, and Interfaces (Kluwer Academic Publishers, Boston/London/Dordrecht, 1997).Google Scholar
9 Andersen, O.K., Jepsen, O. and Sob, M., in Lecture Notes in Physics: Electronic Band Structure and Its Applications, eds. Yussouff, M. (Springer-Verlag, Berlin, 1987).Google Scholar
10 Lambrecht, W.R.L. and Andersen, O.K., Phys. Rev. B 34, 2439 (1986).Google Scholar
11 Andersen, O.K., Pawlowska, Z. and Jepsen, O., Phys. Rev. B 34, 5253 (1986).Google Scholar
12 Pettifor, D.G., J. Phys. F 7, 613 (1977);Google Scholar
Pettifor, D.G., J. Phys. F 7, 1009 (1977);Google Scholar
Pettifor, D.G., J. Phys. F 8, 219 (1978).Google Scholar
13 Andersen, O.K. and Woolley, R.G., Mol. Phys. 26, 905 (1973).Google Scholar
14 Haydock, R. in Solid State Physics 35 edited by Ehrenreich, H., Seitz, F., and Turnbull, D. (Springer Verlag, Berlin, 1980) p. 129.Google Scholar
15 Nowak, H.J., Andersen, O.K., Fujiwara, T., Jepsen, O. and Vargas, P., Phys. Rev. B 44, 3577 (1991);Google Scholar
Vargas, P., C., in Lectures on Methods of Electronic Structure Calculations, edited by Kumar, V., Andersen, O.K., and Mookerjee, A. (World Scientific Publishing Co., Singapore, 1994), pp. 147–191;Google Scholar
Frota-Pessoa, S., Phys. Rev. B 36, 904 (1987);Google Scholar
Bose, S.K., Jepsen, O., and Andersen, O.K., Phys. Rev. B 48, 4265 (1993).Google Scholar
16 The Stuttgart TB-LMTO program, http://www.mpi-stuttgart.mpg.de Google Scholar
17 Jepsen, O. and Andersen, O.K., Z. Phys. B 97, 35 (1995).Google Scholar
18 Gunnarsson, O., Harris, J., and Jones, R.O., Phys. Rev. B 15, 3027 (1977);Google Scholar
Weyrich, K.H., Solid State Commun. 54, 975 (1985);Google Scholar
Springborg, M. and Andersen, O.K., J. Chem. Phys. 87, 7125 (1986);Google Scholar
Methfessel, M., Phys. Rev. 38, 1537 (1988);Google Scholar
Methfessel, M., Rodriguez, C.O., and Andersen, O.K., Phys. Rev. B 40, 2009 (1989); J. Wills (unpublished);Google Scholar
Savrasov, S.Y., Phys. Rev. B 54, 16470 (1996).Google Scholar
19 An exception is: Vitos, L., Kollar, J., and Skriver, H.L., Phys. Rev. B 49, 16694 (1994).Google Scholar
20 Tank, R.W., Andersen, O. K., Krier, G., Arcangeli, C., and Jepsen, O. (unpublished).Google Scholar
21 In order to make K positive-, rather than negative definite, we have defined K with the opposite sign as in Ref. 3.Google Scholar
22 This neglects the high-order term Google Scholar
23 Andersen, O. K., Jepsen, O., Liechtenstein, A. I., and Mazin, I. I.; Phys. Rev. B 49, 4145 (1994);Google Scholar
Andersen, O. K., Liechtenstein, A. I., Jepsen, O., and Paulsen, F.; J. Phys. Chem. Solids 56, 1573 (1995).Google Scholar
24 Saha-Dasgupta, T., Andersen, O. K., Krier, G., Arcangeli, C., Tank, R.W., Jepsen, O., and Dasgupta, I. (unpublished).Google Scholar
25 Müller, T. F. A., Anisimov, V., Rice, T. M., Dasgupta, I., and Saha-Dasgupta, T. (unpublished) cond-mat/9802029.Google Scholar
26 Savrasov, S. Y. and Andersen, O. K., Phys. Rev. Lett. 77, 4430 (1996).Google Scholar
27 Chadi, D. J. and Cohen, M. L., phys. status solidi 68, 405 (1975).Google Scholar
28 Cohen, R. E., Stixrude, L., and Wasserman, E., Phys. Rev. B 56, 8575 (1997).Google Scholar
29 McMahan, A. K. and Klepeis, J. E., Phys. Rev. B 56, 12 250 (1997).Google Scholar
30 Arcangeli, C., Andersen, O.K., and Tank, R.W. (unpublished).Google Scholar