Research Article
On the densest packing of convex discs
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 1-3
-
- Article
- Export citation
On certain infinite products
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 4-10
-
- Article
- Export citation
The average order of magnitude of least primitive roots in algebraic number fields
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 11-25
-
- Article
- Export citation
Class groups of cyclic p-groups
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 26-57
-
- Article
- Export citation
On capitulation in certain Zl-extensions of number fields
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 58-60
-
- Article
- Export citation
Transcendental numbers arising from Drinfeld modules
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 61-66
-
- Article
- Export citation
Generalized irregular primes
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 67-73
-
- Article
- Export citation
A counterexample to elimination in systems of algebraic differential equations
- Part of:
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 74-76
-
- Article
- Export citation
On hypersonic self-induced separation, hydraulic jumps and boundary layers with algebraic growth
- Part of:
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 77-93
-
- Article
- Export citation
On the general solution of a linear second order equation with variable coefficients
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 94-103
-
- Article
- Export citation
On the distribution of √p modulo one
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 104-116
-
- Article
- Export citation
Some metrical properties of continued fractions
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 117-132
-
- Article
- Export citation
On Kruskal's cascades and counting containments in a set of subsets
- Part of:
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 133-141
-
- Article
- Export citation
An analytic inequality
- Part of:
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 142-152
-
- Article
- Export citation
Front matter
MTK volume 30 issue 1 Front matter
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. f1-f2
-
- Article
-
- You have access
- Export citation
Back matter
MTK volume 30 issue 1 Back matter
-
- Published online by Cambridge University Press:
- 26 February 2010, p. b1
-
- Article
-
- You have access
- Export citation

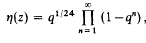
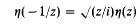
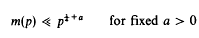
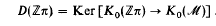
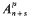 for large enough
for large enough 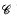 be a smooth projective, geometrically irreducible curve over a finite field
be a smooth projective, geometrically irreducible curve over a finite field 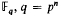 . We fix a rational point ∞on
. We fix a rational point ∞on 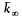 whose elements will be called “numbers”.
whose elements will be called “numbers”.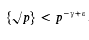
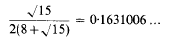
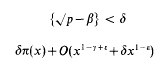
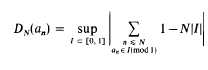
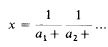
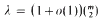 ,
,