Research Article
Görtler vortices in growing boundary layers: The leading edge receptivity problem, linear growth and the nonlinear breakdown stage
- Part of:
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 151-189
-
- Article
- Export citation
The k-dimensional Duffin and Schaeffer conjecture
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 190-200
-
- Article
- Export citation
Exponential sums and rational points on complete intersections
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 201-208
-
- Article
- Export citation
A p-adic approach to solutions of a polynomial congruence modulo pα
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 209-216
-
- Article
- Export citation
The potential due to a circular parallel plate condenser
- Part of:
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 217-231
-
- Article
- Export citation
Minkowski surface area under affine transformations
- Part of:
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 232-238
-
- Article
- Export citation
A note on a problem of H. Busemann and C. M. Petty concerning sections of symmetric convex bodies
- Part of:
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 239-244
-
- Article
- Export citation
On the union of convex bodies with no interior point in common
- Part of:
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 245-250
-
- Article
- Export citation
The Szendrei expansion of a semigroup
- Part of:
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 251-260
-
- Article
- Export citation
Small zeros of quadratic congruences modulo pq
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 261-272
-
- Article
- Export citation
On the lower bound sieve
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 273-286
-
- Article
- Export citation
A zero-free region for the Hecke L-functions
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 287-304
-
- Article
- Export citation
Sums of powers of the zeros of the Bessel polynomials
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 305-315
-
- Article
- Export citation
On the dimension of product measures
- Part of:
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 316-323
-
- Article
- Export citation
A nonparallel cylinder packing with positive density
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 324-331
-
- Article
- Export citation
Book Reviews
BOOK REVIEWS - D. J. Acheson. Elementary Fluid Dynamics. Clarendon Press. 1990, 397 pp., £15. - C. D. Aliprantis and O. Burkinshaw. Principles of Real Analysis. 2nd Edition. Academic Press. 1990, 295 pp., $39.95. - C. D. Aliprantis and O. Burkinshaw. Problems in Real Analysis. Academic Press. 1990, 285 pp., $29.95. - M. Aoki. Optimization of Stochastic Systems: Topics in Discrete-Time Dynamics. Academic Press. 1989, 417 pp., $64.95. - J. Borwein and P. Borwein. A Dictionary of Real Numbers. Wadsworth and Brooks/Cole. 1990, 424 pp., £55-50. - Y. A. Brychkov and A. P. Prudnikov. Integral Transforms of Generalized Functions. Gordon & Breach. 1989, 343 pp., $140. - A. J. Chorin. Computational Fluid Mechanics: Selected Papers. Academic Press. 1989, 223 pp., $35. - C. Clapham. The Concise Oxford Dictionary of Mathematics. Oxford University Press. 1990, 204 pp., £4-95. - P. Constantin and C. Foias. Navier-Stokes Equations. University of Chicago Press. 1988, 190 pp., £27-95. - S. Dineen. The Schwarz Lemma. Clarendon Press. 1989, 248 pp., £25. - P. Dita and V. Georgescu, Editors. Conformal Invariance and String Theory. Academic Press. 1989, 557 pp., $59.95. - L. Eldén and L. Wittmeyer-Koch. Numerical Analysis–an Introduction. Academic Press. 1990, 347 pp., $39.95. - K. D. Elworthy and J.-C. Zambrini. Stochastic Analysis, Path Integration and Dynamics. Longman. 1989, 263 pp., £18. - R. V. Gamkrelidze, Editor. Analysis I: Integral Representations and Asymptotic Methods. Springer. 1989, 238 pp., DM 128. - S. Gelbart and F. Shahidi. Analytic properties of automorphic L-functions. Academic Press. 1988, 131 pp., $18.75. - T. A. Grandine. The Numerical Methods Programming Projects Book. Oxford. 1990, 146 pp., £9-95 - M. H. J. Gruber. Regression Estimators: a Comparative Study. Academic Press. 1990, 347 pp., $49.95. - F. R. Harvey. Spinors and Calibrations. Academic Press. 1990, 313 pp., $39.95. - W. K. Hayman. Subharmonic Functions, Vol. 2. Academic Press. 1989, 590 pp., £53-50. - J. Kevorkian. Partial Differential Equations: Analytical Solution Techniques. Wadsworth and Brooks/Cole. 1990, 547 pp., £14-95. - H.-O. Kreiss and J. Lorenz. Initial-Boundary Value Problems and the Navier Stokes Equations. Academic Press. 1989, 402 pp., $54.50. - S. Lang. A First Course in Calculus. Fifth Edition. Springer. 1986, 280 pp., DM 128. - P. D. Lax and R. S. Phillips. Scattering Theory, 2nd Edition. Academic Press. 1989, 309 pp., $44.95. - J. C. Morgan II. Point set theory. Marcel Dekker. 1990, 296 pp., $119.50. - M. Pavel. Fundamentals of Pattern Recognition. Marcel Dekker. 1989, 183 pp., $107.50. - J. Roitman. Introduction to Modern Set Theory. Wiley. 1990, 156 pp., £32-15. - C. Rogers and W. F. Ames. Nonlinear Boundary Value Problems in Science and Engineering. Academic Press. 1989, 417 pp., $69.9 - D. E. Rowe and J. Mccleary, Editors. The History of Modern Mathematics. Vol. II: Institutions and Applications. Academic Press. 1989, 325 pp., $37.50. - D. Ruelle. Elements of Differentiable Dynamics and Bifurcation Theory. Academic Press. 1989, 187 pp., $27.50 - Y. A. Ryzhov, U. G. Pirumov and V. N. Gorbunov. Nonequilibrium condensation in high-speed gas flows. Gordon and Breach. 1989, 290 pp., $199. - Y. G. Sinai, Editor. Dynamical Systems II. Springer. 1989, 281 pp., DM 128. - V. I. Arnold and S. P. Novikov, Editors. Dynamical Systems IV. Springer. 1990, 283 pp., DM 128. - P. Smith and R. C. Smith. Mechanics. 2nd Edition. Wiley. 1990, 316 pp., £13-95. - G. Stépán. Retarded dynamical systems: stability and characteristic functions. Longman. 1989, 151 pp., £16-50. - G. Toth. Harmonic maps and minimal immersions through representation theory. Academic Press. 1990, 154 pp., $24.95. - M. Vaughan-Lee. The restricted Burnside problem. Oxford University Press. 1990, 209 pp., £27-50. - F. Verhulst. Nonlinear Differential Equations and Dynamical Systems. Springer. 1990, 277 pp., DM38. - A. G. Vitushkin, Editor. Several Complex Variables, I. Springer. 1990, 248 pp., DM128. - W. L. Wood. Practical Time-stepping Schemes. Clarendon Press. 1990, 373 pp., £17-50. - H. S. Wilf. Generating functionology. Academic Press. 1990, 184 pp., $29.95. - M. Young. The Technical Writer's Handbook. Oxford University Press. 1989, 232 pp., £14-95. - E. Zauderer. Partial Differential Equations of Applied Mathematics, 2nd Edition. Wiley. 1989, 891 pp., £51.30 hardback, £29.75 paperback.
-
- Published online by Cambridge University Press:
- 07 April 2017, pp. 332-340
-
- Article
- Export citation
Index
Index to volume 37
-
- Published online by Cambridge University Press:
- 26 February 2010, p. 341
-
- Article
- Export citation
Front matter
MTK volume 37 issue 2 Front matter
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. f1-f2
-
- Article
-
- You have access
- Export citation

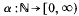 the statement;
the statement;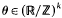 there are infinitely many natural numbers
there are infinitely many natural numbers 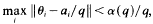
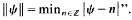
 diverges.
diverges.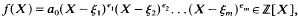 where
where  . Then
. Then 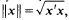 , and
, and 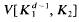 for the mixed volume
for the mixed volume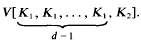
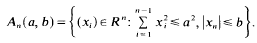
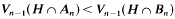 for every (
for every (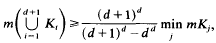
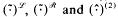 introduced in [3] have proved to be of particular interest when applied to groups. In fact, as shown in [4],
introduced in [3] have proved to be of particular interest when applied to groups. In fact, as shown in [4], 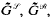
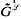 is an
is an 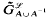 which is a subsemigroup of
which is a subsemigroup of 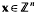 such that
such that
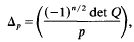
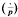 is the Legendre symbol.
is the Legendre symbol.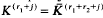 . The conjugates of the number μ in
. The conjugates of the number μ in 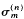 be the sum of the
be the sum of the 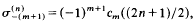
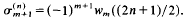
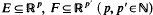 then
then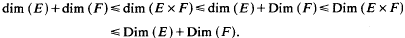
 of pairwise disjoint congruent infinite circular cylinders such that no two cylinders of
of pairwise disjoint congruent infinite circular cylinders such that no two cylinders of