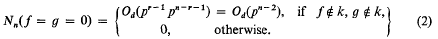Research Article
Selberg's sieve with weights
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 1-22
-
- Article
- Export citation
On the number of primes p for which p+a has a large prime factor
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 23-27
-
- Article
- Export citation
Planar maps with prescribed types of vertices and faces
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 28-36
-
- Article
- Export citation
On the slow motion generated in a viscous fluid by the approach of a sphere to a plane wall or stationary sphere
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 37-49
-
- Article
- Export citation
On controllable deformations in a mixture of two non-linear elastic solids
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 50-56
-
- Article
- Export citation
An exceptional set for Hausdorff dimension
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 57-58
-
- Article
- Export citation
On Liouville's extension of Abel's integral equation
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 59-85
-
- Article
- Export citation
Sums and products of functions in the MacLane class A
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 86-87
-
- Article
- Export citation
The Cremona transformation of S6 by quadrics through a normal elliptic septimic scroll 1R7
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 88-97
-
- Article
- Export citation
The distribution of solutions of congruences: corrigendum and addendum
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 98-100
-
- Article
- Export citation
An analogue of a problem of Littlewood
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 101-105
-
- Article
- Export citation
On the flow near the trailing edge of a flat plate II
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 106-121
-
- Article
- Export citation
Wing-body interaction in supersonic flow
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 122-142
-
- Article
- Export citation
Front matter
MTK volume 16 issue 1 Front matter
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. f1-f2
-
- Article
-
- You have access
- Export citation

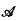 be a (finite) non-empty sequence of integers, and let
be a (finite) non-empty sequence of integers, and let 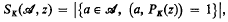
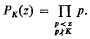
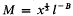
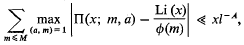
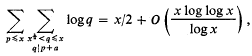
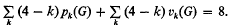
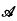 be the class of non-constant functions
be the class of non-constant functions 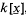 , where
, where 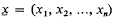 .
. 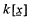 with no non-constant common factor in
with no non-constant common factor in 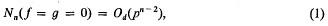
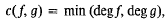
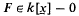 and
and