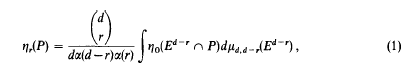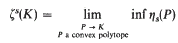Research Article
On the chromatic number of binary matroids
- Part of:
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 1-9
-
- Article
- Export citation
L-Series for genera at s = 1
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 10-16
-
- Article
- Export citation
Locally minimal Epstein zeta functions
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 17-24
-
- Article
- Export citation
Small fractional parts of quadratic forms in many variables
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 25-29
-
- Article
- Export citation
Small solutions of quadratic and quartic congruences
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 30-45
-
- Article
- Export citation
Rarefaction indices
- Part of:
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 46-57
-
- Article
- Export citation
Shadow-boundaries and cuts of convex polytopes
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 58-63
-
- Article
- Export citation
A graph and its complement with specified properties V: The self-complement index
- Part of:
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 64-68
-
- Article
- Export citation
Proof of D. J. Newman's coprime mapping conjecture
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 69-83
-
- Article
- Export citation
Popular values of Euler's function
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 84-89
-
- Article
- Export citation
Sections of Sets of zero Lebesgue measure
- Part of:
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 90-96
-
- Article
- Export citation
Skeleta and sections of convex bodies
- Part of:
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 97-103
-
- Article
- Export citation
On the slow viscous rolling of a sphere in contact with a permeable surface
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 104-112
-
- Article
- Export citation
Convex bodies which tile space by translation
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 113-121
-
- Article
- Export citation
The d – 2 Skeletons of polytopal approximations to a convex body in Ed
- Part of:
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 122-133
-
- Article
- Export citation
Front matter
MTK volume 27 issue 1 Front matter
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. f1-f2
-
- Article
-
- You have access
- Export citation

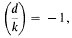 then
then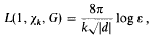
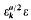 belongs to the field
belongs to the field 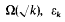 is the fundamental unit of
is the fundamental unit of 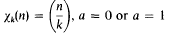 depending on whether there are an even number or an odd number of classes per genus in
depending on whether there are an even number or an odd number of classes per genus in 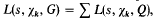 the summation being over a complete set of inequivalent forms in the genus
the summation being over a complete set of inequivalent forms in the genus 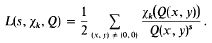
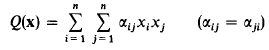
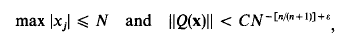
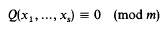
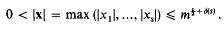
 of
of