Research Article
The lower bound theorem for centrally symmetric simple polytopes
- Part of:
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 231-240
-
- Article
- Export citation
Families of congruent curves and applications
- Part of:
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 241-252
-
- Article
- Export citation
On the Steinhaus tiling problem
- Part of:
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 253-280
-
- Article
- Export citation
The behaviour of the Riemann zeta-function on the critical line
- Part of:
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 281-313
-
- Article
- Export citation
Lower bounds for multilinear forms defined on Hilbert Spaces
- Part of:
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 315-322
-
- Article
- Export citation
Continuous functions on products of compact Hausdorff spaces
- Part of:
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 323-330
-
- Article
- Export citation
Compact measure spaces
- Part of:
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 331-336
-
- Article
- Export citation
On the convergence of Σ∞n = 1f(nx) for measurable functions
- Part of:
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 337-341
-
- Article
- Export citation
Locally uniformly rotund norms
- Part of:
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 343-358
-
- Article
- Export citation
On some questions of Erdős and Graham about Egyptian fractions
- Part of:
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 359-372
-
- Article
- Export citation
On extending Artin's conjecture to composite moduli
- Part of:
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 373-390
-
- Article
- Export citation
Sign changes of error terms related to the Euler function
- Part of:
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 391-395
-
- Article
- Export citation
On the scarcity of powerful binomial coefficients
- Part of:
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 397-410
-
- Article
- Export citation
On integers with identical digits
- Part of:
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 411-417
-
- Article
- Export citation
On the divisor function d(n): II
- Part of:
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 419-423
-
- Article
- Export citation
Prüfer domains and pure submodules of direct sums of ideals
- Part of:
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 425-432
-
- Article
- Export citation
Global solutions to the discrete coagulation equations
- Part of:
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 433-442
-
- Article
- Export citation
On the reducibility of a class of linear differential equations with quasiperiodic coefficients
- Part of:
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 443-451
-
- Article
- Export citation
Solvability in Lp of the Neumann problem for a singular non-homogeneous Sturm-Liouville equation
- Part of:
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 453-470
-
- Article
- Export citation
Book-Reviews
R. B. Bapat AND T. E. S. Raghavan. Nonnegative Matrices and Applications. Encyclopedia of Mathematics and Its Applications, 64. Cambridge University Press. 1997, 336 pp., ISBN 0 521 57167 7 (hardback), £45. - L. J. Billera, A. Björner, C. Greene, R. E. Simion and R. P. Stanley (Eds.). New Perspectives in Algebraic Combinatorics. Cambridge University Press. 1999, 345 pp., ISBN 0 521 77087 4 (hardback), £32·50. - Robert Bix. Conies and Cubics, a Concrete Introduction to Algebraic Curves. Springer Undergraduate Texts in Mathematics. Springer-Verlag. 1998, 289 pp., ISBN 0 387 98401 1 (hardback), £37·50. - A. Björner, M. Las Vergnas, B. Sturmfels, N. White and G. Ziegler. Oriented Matroids (2nd Edition). Encyclopedia of Mathematics and Its Applications, 46. Cambridge University Press. 1999, 548 pp., ISBN 0 521 77750 X (paperback), £30. - David M. Bressoud. Proofs and Configurations (the Story of the Alternating Sign Matrix Conjecture). Cambridge University Press. 1999, 274 pp.. ISBN 0 521 66170 6 (hardback), £47·50; 0 521 66646 5 (paperback), £17·95. - G. P. Csicsery. N is a number: a Portrait of Paul Erdőds. A Documentary Film. Springer Videomath. 1999, 57 min., ISBN 3 540 92642 9, £25·83. - H. Davenport. The Higher Arithmetic (7th edition). Cambridge University Press. 1999, 241 pp., ISBN 0 521 63269 2 (hardback), £45; 0 521 63446 6 (paperback), £16·95. - J. D. Dixon, M. P. F. Du Sautoy, A. Mann and D. Segal. Analytic Pro-p groups (2nd edition). Cambridge Studies in Advanced Mathematics, 61. Cambridge University Press. 1999, 368 pp., ISBN 0 521 65011 9 (hardback). £37·50. - D. Eisenbud and J. Harris. The Geometry of Schemes. Graduate Texts in Mathematics, 197. Springer-Verlag (New York, Berlin, etc.). 1999, 294 pp., ISBN 0 387 98638 3 (hardback), £48; 0 387 98637 5 (paperback), £18. - R. Feres. Dynamical Systems and Semisimple Groups: an Introduction. Cambridge Tracts in Mathematics, 126. Cambridge University Press. 1998, 245 pp., ISBN 0 521 59162 7 (hardback), £35. - G. T. Gilbert and R. L. Hatcher. Mathematics beyond the Numbers. Wiley–Interscience (New York). 1999, 687 pp., ISBN 0 471 13934 3 (hardback), £39·95. - D. Gusfield. Algorithms on Strings, Trees and Sequences: Computer Science and Computational Biology. Cambridge University Press. 1997, 534 pp., ISBN 0 521 58519 8 (hardback), £40. - J. Harris and I. Morrison. Moduli of Curves. Graduate Texts in Mathematics. Springer-Verlag. 1998, 366 pp., ISBN 0 387 98438 0 (hardback), £45·50; 0 387 98429 1 (paperback), £28·50. - A. Ivanov. Geometry of Sporadic Groups, I, Petersen and Tilde Geometries. Encyclopedia of Mathematics and Its Applications, 76. Cambridge University Press. 1999, 408 pp., ISBN 0 521 41362 1 (hardback), £45. - P.-L. Lions. Mathematical Topics in Fluid Mechanics, Vol. 2. Clarendon Press (Oxford). 1998, 348 pp., ISBN 0 198 51488 3 (hardback), £42. - Isaac Newton. The Principia: Mathematical Principles of Natural Philosophy. A New Translation by I. Bernard Cohen and Anne Whitman, assisted by Julia Budenz. (Preceded by a Guide to Newton's Principia by I. Bernard Cohen.) University of California Press (Berkeley). 1999, 971 pp.. ISBN 0 520 08816 6 (hardback), £47; 0 520 08817 4 (paperback), £22·50; 0 520 00929 0 (paperback), £11·95. - W. Keith Nicholson. Introduction to Abstract Algebra (2nd edition). Wiley-Interscience (New York). 1999, 599 pp., ISBN 0 471 33109 0 (hardback). £58·50. - H. Scheffé. The Analysis of Variance. Wiley–Interscience (New York). 1999. 477 pp., ISBN 0 471 34505 9 (paperback), £32·50. - S. Stahl. Real Analysis: a Historical Approach. Wiley–Interscience (New York). 1999, 269 pp., ISBN 0 471 31852 3 (hardback), £51·95. - Manfred Stern. Semimodular Lattices. Encyclopedia of Mathematics and Its Applications, 73. Cambridge University Press. 1999, 370 pp., ISBN 0 521 46105 7 (hardback), £50.
-
- Published online by Cambridge University Press:
- 08 April 2017, pp. 471-475
-
- Article
- Export citation

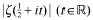 between successive zeros. Our results are to be independent of any unproved hypothesis. Put
between successive zeros. Our results are to be independent of any unproved hypothesis. Put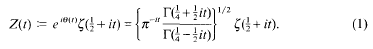
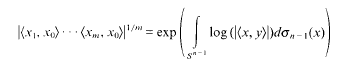
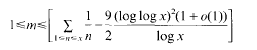
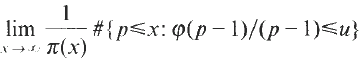
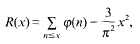
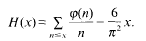
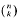 with 3≤
with 3≤ . Unconditionally, it is shown that there are
. Unconditionally, it is shown that there are 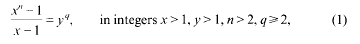
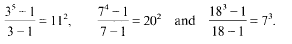
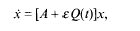
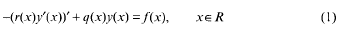
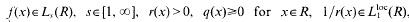 ,
, 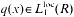 . The inversion problem for (1) is called regular in
. The inversion problem for (1) is called regular in 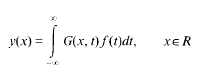
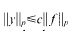 . Here
. Here 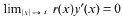 for any
for any