Research Article
On the large sieves of Linnik and Rényi
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 1-9
-
- Article
- Export citation
On badly approximable numbers
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 10-20
-
- Article
- Export citation
Plasticity theory and multipolar continuum mechanics
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 21-26
-
- Article
- Export citation
A note on linear transversely isotropic fluids
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 27-29
-
- Article
- Export citation
Cubic Diophantine equations: the necessary congruence condition
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 30-38
-
- Article
- Export citation
Cubic Diophantine equations: a supplementary congruence condition
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 39-48
-
- Article
- Export citation
Diffusion from an elevated point source into a turbulent atmosphere
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 49-57
-
- Article
- Export citation
Eigen-functions for the strip problem
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 58-64
-
- Article
- Export citation
On irredundant components of the kernel of an ideal
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 65-72
-
- Article
- Export citation
Metrics for sets of convex bodies
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 73-88
-
- Article
- Export citation
A theorem on convex kernels
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 89-93
-
- Article
- Export citation
Scalar matrix quadratic residues
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 94-96
-
- Article
- Export citation
On the unsteady motion of a rotating fluid in a cavity
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 97-106
-
- Article
- Export citation
Front matter
MTK volume 12 issue 1 Cover and Front matter
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. f1-f4
-
- Article
-
- You have access
- Export citation

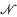 be a non-empty subset of the set of integers
be a non-empty subset of the set of integers
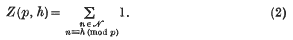
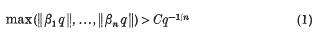
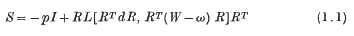
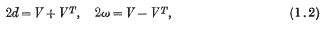
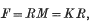
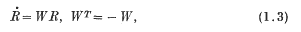
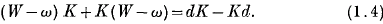
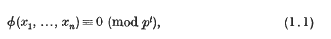

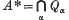 is called the
is called the 