Hostname: page-component-76fb5796d-22dnz Total loading time: 0 Render date: 2024-04-25T12:21:38.912Z Has data issue: false hasContentIssue false
  • English
  • Français

ZEROS OF CERTAIN COMBINATIONS OF EISENSTEIN SERIES

Part of: Discontinuous groups and automorphic forms

Published online by Cambridge University Press:  10 August 2017

Sarah Reitzes ,
Polina Vulakh  and
Matthew P. Young
Sarah Reitzes
Affiliation:
Department of Mathematics, The University of Chicago, 5734 S University Ave, Chicago IL 60637, U.S.A. email sreitzes@math.uchicago.edu
Polina Vulakh
Affiliation:
Bard College, U.S.A. email pv2315@bard.edu
Matthew P. Young
Affiliation:
Department of Mathematics, Texas A&M University, College Station, TX 77843-3368, U.S.A. email myoung@math.tamu.edu
Get access

Abstract

We prove that if 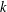$k$ and 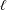$\ell$ are sufficiently large, then all the zeros of the weight 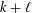$k+\ell$ cusp form 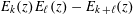$E_{k}(z)E_{\ell }(z)-E_{k+\ell }(z)$ in the standard fundamental domain lie on the boundary. We, moreover, find formulas for the number of zeros on the bottom arc with 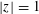$|z|=1$, and those on the sides with 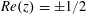$Re(z)=\pm 1/2$. One important ingredient of the proof is an approximation of the Eisenstein series in terms of the Jacobi theta function.

MSC classification

Primary: 11F11: Holomorphic modular forms of integral weight
Type
Research Article
Information
Mathematika , Volume 63 , Issue 2 , 2017 , pp. 666 - 695
Copyright
Copyright © University College London 2017 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Asai, T., Kaneko, M. and Ninomiya, H., Zeros of certain modular functions and an application. Comment. Math. Univ. St. Pauli 46(1) 1997, 93–101.Google Scholar
Duke, W. and Jenkins, P., On the zeros and coefficients of certain weakly holomorphic modular forms. Pure Appl. Math. Q. 4(4) 2008, 1327–1340 Special Issue: In honor of Jean-Pierre Serre. Part 1.CrossRefGoogle Scholar
Ghosh, A. and Sarnak, P., Real zeros of holomorphic Hecke cusp forms. J. Eur. Math. Soc. (JEMS) 14(2) 2012, 465–487.Google Scholar
Gradshteyn, I. S. and Ryzhik, I. M., Table of Integrals, Series, and Products, 6th edn., Academic Press, Inc. (San Diego, CA, 2000) Translated from the Russian, Translation edited and with a preface by Alan Jeffrey and Daniel Zwillinger.Google Scholar
Gun, S., On the zeros of certain cusp forms. Math. Proc. Cambridge Philos. Soc. 141(2) 2006, 191–195.Google Scholar
Holowinsky, R. and Soundararajan, K., Mass equidistribution for Hecke eigenforms. Ann. of Math. (2) 172(2) 2010, 1517–1528.Google Scholar
Jenkins, P. and Pratt, K., Interlacing of zeros of weakly holomorphic modular forms. Proc. Amer. Math. Soc. B 1 2014, 63–77.Google Scholar
Jermann, J., Interlacing property of the zeros of j n (𝜏). Proc. Amer. Math. Soc. 140(10) 2012, 3385–3396.Google Scholar
Kohnen, W., Zeros of Eisenstein series. Kyushu J. Math. 58(2) 2004, 251–256.Google Scholar
Lindenstrauss, E., Invariant measures and arithmetic quantum unique ergodicity. Ann. of Math. (2) 163(1) 2006, 165–219.CrossRefGoogle Scholar
Luo, W. and Sarnak, P., Quantum ergodicity of eigenfunctions on PSL2(Z)\H 2 . Publ. Math. Inst. Hautes Études Sci. 81 1995, 207–237.Google Scholar
Nozaki, H., A separation property of the zeros of Eisenstein series for SL(2, ℤ). Bull. Lond. Math. Soc. 40(1) 2008, 26–36.Google Scholar
Rankin, F. K. C. and Swinnerton-Dyer, H. P. F., On the zeros of Eisenstein series. Bull. Lond. Math. Soc. 2 1970, 169–170.Google Scholar
Rudnick, Z., On the asymptotic distribution of zeros of modular forms. Int. Math. Res. Not. IMRN 2005(34) 2005, 2059–2074.Google Scholar
Rudnick, Z. and Sarnak, P., The behaviour of eigenstates of arithmetic hyperbolic manifolds. Comm. Math. Phys. 161(1) 1994, 195–213.Google Scholar
Soundararajan, K., Quantum unique ergodicity for SL2(Z)\H . Ann. of Math. (2) 172(2) 2010, 1529–1538.CrossRefGoogle Scholar