Hostname: page-component-76fb5796d-dfsvx Total loading time: 0 Render date: 2024-04-25T17:46:12.401Z Has data issue: false hasContentIssue false
  • English
  • Français

TRIANGLES CAPTURING MANY LATTICE POINTS

Part of: Geometry of numbers Additive number theory; partitions Polytopes and polyhedra Discrete geometry

Published online by Cambridge University Press:  25 April 2018

Nicholas F. Marshall  and
Stefan Steinerberger
Nicholas F. Marshall
Affiliation:
Department of Mathematics, Yale University, New Haven, CT 06511, U.S.A. email nicholas.marshall@yale.edu
Stefan Steinerberger
Affiliation:
Department of Mathematics, Yale University, New Haven, CT 06511, U.S.A. email stefan.steinerberger@yale.edu
Get access

Abstract

We study a combinatorial problem that recently arose in the context of shape optimization: among all triangles with vertices 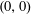$(0,0)$, 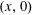$(x,0)$, and 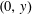$(0,y)$ and fixed area, which one encloses the most lattice points from 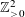$\mathbb{Z}_{{>}0}^{2}$? Moreover, does its shape necessarily converge to the isosceles triangle 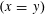$(x=y)$ as the area becomes large? Laugesen and Liu suggested that, in contrast to similar problems, there might not be a limiting shape. We prove that the limiting set is indeed non-trivial and contains infinitely many elements. We also show that there exist “bad” areas where no triangle is particularly good at capturing lattice points and show that there exists an infinite set of slopes 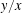$y/x$ such that any associated triangle captures more lattice points than any other fixed triangle for infinitely many (and arbitrarily large) areas; this set of slopes is a fractal subset of 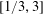$[1/3,3]$ and has Minkowski dimension of at most 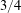$3/4$.

MSC classification

Primary: 11P21: Lattice points in specified regions 52B05: Combinatorial properties (number of faces, shortest paths, etc.) 52C05: Lattices and convex bodies in $2$ dimensions
Secondary: 11H06: Lattices and convex bodies 90C27: Combinatorial optimization
Type
Research Article
Information
Mathematika , Volume 64 , Issue 2 , 2018 , pp. 551 - 582
Copyright
Copyright © University College London 2018 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Antunes, P. R. S. and Freitas, P., Optimal spectral rectangles and lattice ellipses. Proc. R. Soc. Lond. Ser. A 469(2150) 2012.Google Scholar
Antunes, P. R. S. and Freitas, P., Optimisation of eigenvalues of the Dirichlet Laplacian with a surface area restriction. Appl. Math. Optim. 73(2) 2016, 313–328.CrossRefGoogle Scholar
Ariturk, S. and Laugesen, R. S., Optimal stretching for lattice points under convex curves. Port. Math. 74(2) 2017, 91–114.Google Scholar
Beck, M. and Robins, S., Computing the Continuous Discretely (Undergraduate Texts in Mathematics), Springer (New York, 2007).Google Scholar
Berger, A., The eigenvalues of the Laplacian with Dirichlet boundary condition in ℝ2 are almost never minimized by disks. Ann. Global Anal. Geom. 47(3) 2015, 285–304.Google Scholar
Besicovitch, A. S., On the linear independence of fractional powers of integers. J. Lond. Math. Soc. (2) 15 1940, 3–6.Google Scholar
Boreico, I., Linear independence of radicals. The Harvard College Mathematics Review 2(1) 2008, 87–92.Google Scholar
Bucur, D. and Freitas, P., Asymptotic behaviour of optimal spectral planar domains with fixed perimeter. J. Math. Phys. 54(5) 2013,053504.CrossRefGoogle Scholar
Kronecker, L., Näherungsweise ganzzahlige Auflösung linearer Gleichungen. Berl. Ber. 1179–1193 1884, 1271–1299.Google Scholar
Kuipers, L. and Niederreiter, H., Uniform Distribution of Sequences (Pure and Applied Mathematics), Wiley-Interscience (1974).Google Scholar
Laugesen, R. and Liu, S., Optimal stretching for lattice points and eigenvalues. Ark. Mat. (to appear).Google Scholar
Pick, G., Geometrisches zur Zahlenlehre. Sitzungsberichte des deutschen naturwissenschaftlich-medicinischen Vereines für Böhmen Lotos in Prag 19 1899, 311–319.Google Scholar
van den Berg, M., Bucur, D. and Gittins, K., Maximising Neumann eigenvalues on rectangles. Bull. Lond. Math. Soc. 48(5) 2016, 877–894.Google Scholar
van den Berg, M. and Gittins, K., Minimising Dirichlet eigenvalues on cuboids of unit measure. Mathematika 63(2) 2017, 469–482.Google Scholar
Weyl, H., Über die Gleichverteilung von Zahlen mod. Eins. Math. Ann. 77(3) 1916, 313–352.Google Scholar