Hostname: page-component-76fb5796d-skm99 Total loading time: 0 Render date: 2024-04-25T14:39:13.233Z Has data issue: false hasContentIssue false
  • English
  • Français

Small differences between consecutive primes

Published online by Cambridge University Press:  26 February 2010

M. N. Huxley
M. N. Huxley
Affiliation:
University College, Cardiff.
Get access

Extract

Let pn denote the n-th prime number, and let

It follows from the prime number theorem that E ≤ 1. Erdős used a sieve argument to show that E < 1, and Rankin and Ricci gave the explicit estimates E ≤ 57/59 and E ≤ 15/16 respectively. A more powerful approach used by Hardy and Little-wood and by Rankin depended on hypotheses about the zeros of L-functions until Bombieri's Theorem was found. With its aid Bombieri and Davenport [1] proved that

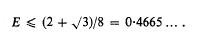
A fuller history, with bibliography, is to be found in [1]

Type
Research Article
Information
Mathematika , Volume 20 , Issue 2 , December 1973 , pp. 229 - 232
Copyright
Copyright © University College London 1973

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1. Bombieri, E. and Davenport, H., “Small differences between prime numbers”, Proc. Royal Soc. A293 (1966), 1–18.Google Scholar
2. Huxley, M. N., “On the differences of primes in arithmetical progressions”, Acta Arithmetica, 15 (1969), 367–392.CrossRefGoogle Scholar
3. Pilt'ai, G. Z., “On the size of the difference between consecutive primes”, Issledovania po teorii chisel, 4 (1972), 73–79.Google Scholar