Hostname: page-component-76fb5796d-vfjqv Total loading time: 0 Render date: 2024-04-27T00:33:26.566Z Has data issue: false hasContentIssue false
  • English
  • Français

Radial variation of functions in Dirichlet-type spaces

Part of: Series expansions

Published online by Cambridge University Press:  26 February 2010

J. B. Twomey
J. B. Twomey
Affiliation:
Department of Mathematics, University College Cork, Ireland.
Get access

Extract

Let W denote a positive, increasing and continuous function on [1, ∞]. We write 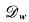to denote the Dirichlettype space of functions f that are holomorphic in the unit disc 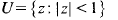and for which

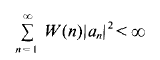
Where 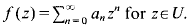If W(x) = x for all x, then 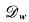is the classicial Dirichlet space for which 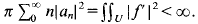Note also that 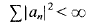for every 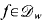so, by Fatu's theoreum, every function in 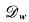. ha finite radial(and angular) limits a.e. on the boundary of U. The question of the existence a.e. on ∂U of certain tangential limits for functions in 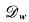has been considered in [6,11], but we shall be concerned here with the radial variation

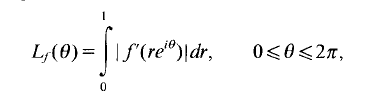
i.e., the length of the image of the ray from 0 to eiθ under the mapping w = f(z), and, in particular, with the size of the set of values of θ for which Lf(θ) can be infinite when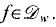

MSC classification

Secondary: 30B30: Boundary behavior of power series, over-convergence
Type
Research Article
Information
Mathematika , Volume 44 , Issue 2 , December 1997 , pp. 267 - 277
Copyright
Copyright © University College London 1997

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1.Beurling, A.. Ensembles exceptionnels. Ada Math., 72 (1940), 1–13.Google Scholar
2.Fejer, L.. Trigonometrische reihen und potenzreihen mit mehrfach monotoner koeffizientenfolge. Trans. Amer. Math. Soc., 39 (1936), 18–59.CrossRefGoogle Scholar
3.Flett, T. M.. A high-indices theorem. Proc. London Math. Soc., (3), 7 (1957), 142–149.Google Scholar
3.Gehring, F. W. and Hayman, W. K.. An inequality in the theory of conformal mapping. J. Pures Appl. (9), 41 (1962), 353–361.Google Scholar
4.Kahane, J.-P. and Salem, R.. Ensembles parfaits et series trigonometriques. Adualites Sci. Ind. No. 1301 (Herman, Paris, 1963).Google Scholar
5.Nagel, A.Rudin, W. and Shapiro, J. H.. Tangential boundary behavior of functions in Dirichlettype spaces. Annals of Maths., 116 (1982), 331–360.CrossRefGoogle Scholar
7.Pommerenke, Ch.. Univalent functions (Vandenhoeck and Ruprecht, Göttingen, 1975).Google Scholar
8.Rudin, W.. The variation of holomorphic functions on tangential boundary curves. Michigan Math. J., 32 (1985), 41–45.CrossRefGoogle Scholar
9.Szalay, I.. On the absolute Cesaro summability of Fourier series. Colloquia Mathematica Societatis Janos Bolyai, 35 (1980), 1171–1181.Google Scholar
10.Twomey, J. B.. On certain sums of Fourier Stieltjes coefficients. Trans. Amer. Math. Soc., 280 (1983), 611–621.CrossRefGoogle Scholar
11.Twomey, J. B.. Tangential limits for certain classes of analytic functions. Mathematika, 36 (1989), 39–49.CrossRefGoogle Scholar
12.Wang, F. T.. Note on the absolute summability of Fourier series. J. London Math. Soc., 16 (1941), 174–176.CrossRefGoogle Scholar
13.Wang, F. T.. The absolute Cesaro summability of trigonometric series. Duke Math. J., 9 (1942), 567–572.CrossRefGoogle Scholar
14.Zygmund, A.. On certain integrals. Trans. Amer. Math. Soc., 55 (1944), 170–204.CrossRefGoogle Scholar
15.Zygmund, A.. Trigonometric series, 2nd ed., vol. 1 (Cambridge Univ. Press, New York, 1959).Google Scholar