Hostname: page-component-848d4c4894-hfldf Total loading time: 0 Render date: 2024-05-10T13:57:38.911Z Has data issue: false hasContentIssue false
  • English
  • Français

ON THE MONTGOMERY–HOOLEY THEOREM IN SHORT INTERVALS

Part of: Additive number theory; partitions Multiplicative number theory

Published online by Cambridge University Press:  12 May 2010

A. Languasco ,
A. Perelli  and
A. Zaccagnini
A. Languasco
Affiliation:
Dipartimento di Matematica Pura e Applicata, Università di Padova, Via Trieste 63, 35121 Padova, Italy (email: languasco@math.unipd.it)
A. Perelli
Affiliation:
Dipartimento di Matematica, Università di Genova, via Dodecaneso 35, 16146 Genova, Italy (email: perelli@dima.unige.it)
A. Zaccagnini
Affiliation:
Dipartimento di Matematica, Università di Parma, Parco Area delle Scienze 53/a, Campus Universitario, 43124 Parma, Italy (email: alessandro.zaccagnini@unipr.it)
Get access

Abstract

We prove two results about the asymptotic formula for 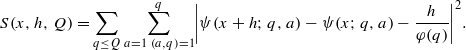The first result is for x7/12+ε≤h≤x and h/(log x)B≤Q≤h, where ε,B>0 are arbitrary constants. For the second result we assume that the Generalized Riemann Hypothesis holds and we obtain a stronger error term and a better uniformity on h.

MSC classification

Secondary: 11N13: Primes in progressions 11P55: Applications of the Hardy-Littlewood method
Type
Research Article
Information
Mathematika , Volume 56 , Issue 2 , July 2010 , pp. 231 - 243
Copyright
Copyright © University College London 2010

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[1]Croft, M. J., Square-free numbers in arithmetic progressions. Proc. Lond. Math. Soc. 30 (1975), 143–159.CrossRefGoogle Scholar
[2]Friedlander, J. B. and Goldston, D. A., Variance of distribution of primes in residue classes. Q. J. Math. 47 (1996), 313–336.CrossRefGoogle Scholar
[3]Goldston, D. A. and Vaughan, R. C., On the Montgomery–Hooley asymptotic formula. In Sieve Methods, Exponential Sums, and their Applications in Number Theory (eds G. R. H. Greaves et al), Cambridge University Press (Cambridge, 1997), 117–142.CrossRefGoogle Scholar
[4]Hooley, C., On theorems of Barban-Davenport-Halberstam type. In Number Theory for the Millennium II (eds M. A. Bennett et al), A. K. Peters (Natick, MA, 2002), 195–228.Google Scholar
[5]Kaczorowski, J., Perelli, A. and Pintz, J., A note on the exceptional set for Goldbach’s problem in short intervals. Monatsh. Math. 116 (1993), 275–282; corrigendum 119 (1995), 215–216.CrossRefGoogle Scholar
[6]Montgomery, H. L., Primes in arithmetic progressions. Michigan Math. J. 17 (1970), 33–39.CrossRefGoogle Scholar
[7]Perelli, A. and Pintz, J., On the exceptional set for Goldbach problem in short interval. J. Lond. Math. Soc. 47 (1993), 41–49.CrossRefGoogle Scholar
[8]Perelli, A., Pintz, J. and Salerno, S., Bombieri’s theorem in short intervals II. Invent. Math. 79 (1985), 1–9.CrossRefGoogle Scholar
[9]Vaughan, R. C., The Hardy–Littlewood Method, 2nd edn., Cambridge University Press (Cambridge, 1997).CrossRefGoogle Scholar
[10]Vaughan, R. C., On a variance associated with the distribution of general sequences in arithmetic progressions. I. Philos. Trans. Roy. Soc. Lond. Ser. A Math. Phys. Eng. Sci. 356 (1998), 781–791.CrossRefGoogle Scholar
[11]Vaughan, R. C., On a variance associated with the distribution of primes in arithmetic progressions. Proc. Lond. Math. Soc. 82 (2001), 533–553.CrossRefGoogle Scholar