Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
De-Jun, Fend
Jun, Wu
Liang, Jyh-Ching
and
Tseng, Shiojenn
1997.
Appendix to the paper by T. Łuczak—A simple proof of the lower.
Mathematika,
Vol. 44,
Issue. 1,
p.
54.
Wang, Bao-Wei
and
Wu, Jun
2008.
Hausdorff dimension of certain sets arising in continued fraction expansions.
Advances in Mathematics,
Vol. 218,
Issue. 5,
p.
1319.
Wu, Jun
2008.
A remark on continued fractions with sequences of partial quotients.
Journal of Number Theory,
Vol. 128,
Issue. 8,
p.
2394.
Hu, Xue-Hai
Wang, Bao-Wei
Wu, Jun
and
Yu, Yue-Li
2008.
Cantor sets determined by partial quotients of continued fractions of Laurent series.
Finite Fields and Their Applications,
Vol. 14,
Issue. 2,
p.
417.
Xu, Jian
2008.
On sums of partial quotients in continued fraction expansions.
Nonlinearity,
Vol. 21,
Issue. 9,
p.
2113.
LIAO, LINGMIN
MA, JIHUA
and
WANG, BAOWEI
2008.
Dimension of some non-normal continued fraction sets.
Mathematical Proceedings of the Cambridge Philosophical Society,
Vol. 145,
Issue. 1,
p.
215.
Wang, B.
and
Wu, J.
2009.
Divergence points with fast growth orders of the partial quotients in continued fractions.
Acta Mathematica Hungarica,
Vol. 125,
Issue. 3,
p.
261.
Wu, Jun
and
Xu, Jian
2011.
On the distribution for sums of partial quotients in continued fraction expansions.
Nonlinearity,
Vol. 24,
Issue. 4,
p.
1177.
Shen, Luming
and
Fang, Kui
2011.
The fractional dimensional theory in Lüroth expansion.
Czechoslovak Mathematical Journal,
Vol. 61,
Issue. 3,
p.
795.
ZHONG, TING
and
TANG, LIANG
2013.
THE SETS OF DIFFERENT CONTINUED FRACTIONS WITH THE SAME PARTIAL QUOTIENTS.
International Journal of Number Theory,
Vol. 09,
Issue. 07,
p.
1855.
Chen, HaiBo
and
Wen, ZhiXiong
2014.
The Hausdorff dimension of certain sets in a class of α-Lüroth expansions.
Science China Mathematics,
Vol. 57,
Issue. 2,
p.
303.
Sun, Yu
and
Wu, Jun
2014.
A dimensional result in continued fractions.
International Journal of Number Theory,
Vol. 10,
Issue. 04,
p.
849.
Peng, Li
2014.
On the hitting depth in the dynamical system of continued fractions.
Chaos, Solitons & Fractals,
Vol. 69,
Issue. ,
p.
22.
Rempe-Gillen, Lasse
and
Urbański, Mariusz
2015.
Non-autonomous conformal iterated function systems and Moran-set constructions.
Transactions of the American Mathematical Society,
Vol. 368,
Issue. 3,
p.
1979.
Liao, Lingmin
and
Rams, Michał
2016.
Upper and lower fast Khintchine spectra in continued fractions.
Monatshefte für Mathematik,
Vol. 180,
Issue. 1,
p.
65.
WANG, BAO-WEI
WU, JUN
and
XU, JIAN
2016.
A generalization of the Jarník–Besicovitch theorem by continued fractions.
Ergodic Theory and Dynamical Systems,
Vol. 36,
Issue. 4,
p.
1278.
Zhang, Zhenliang
2016.
The relative growth rate of the largest digit in continued fraction expansions.
Lithuanian Mathematical Journal,
Vol. 56,
Issue. 1,
p.
133.
Hu, Hui
Yu, Yueli
and
Zhao, Yanfen
2017.
A note on approximation efficiency and partial quotients of Engel continued fractions.
International Journal of Number Theory,
Vol. 13,
Issue. 09,
p.
2433.
WU, JUN
and
XIE, JIAN-SHENG
2017.
Range-renewal structure in continued fractions.
Ergodic Theory and Dynamical Systems,
Vol. 37,
Issue. 4,
p.
1323.
Wu, Xi
Yan, Li
and
Zhong, Ting
2017.
How the dimension of some GCF sets change with proper choice of the parameter function ϵ(k).
Journal of Number Theory,
Vol. 174,
Issue. ,
p.
1.
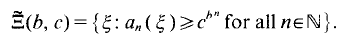
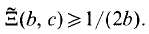 On the other hand, Moorthy [8] showed that dim
On the other hand, Moorthy [8] showed that dim 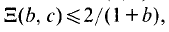 where
where